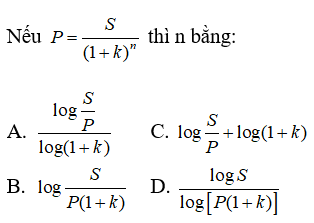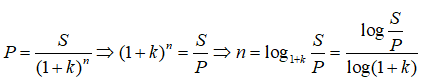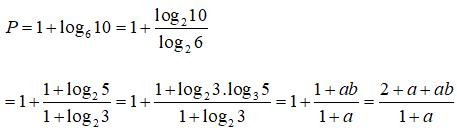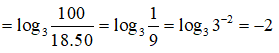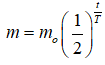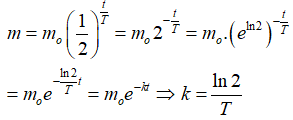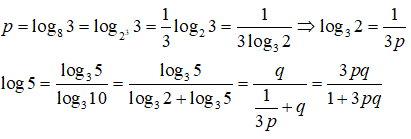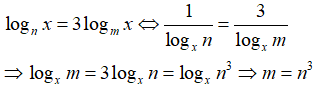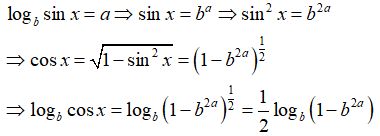Các dạng bài tập về Lôgarit cơ bản (2024) có đáp án

Các dạng bài tập về Lôgarit cơ bản

I. Lí thuyết / Phương pháp giải

1. Khái niệm về lôgarit

- Cho hai số dương a; b với a ≠ 1. Số α thỏa mãn đẳng thức a^α = b được gọi là logarit cơ số a của b và kí hiệu là log_ab.

$\alpha ={\log }_{a}b\iff a^{\alpha }=b$

- Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:

log_a1 = 0; log_aa = 1

$a^{{\log }_{a}b}=b;\log {}_a\left(a^{\alpha }\right)=\alpha$

2. Quy tắc tính logarit

a. Logarit của một tích

– Định lí 1. Cho ba số dương a; b₁ ;b₂ với a ≠ 1. Ta có:

${\log }_a(b_1.b{}_2)={\log }_a{b}_1+{\log }_{a}b{}_2$

Logarit của một tích bằng tổng các logarit.

Ví dụ:

$$\begin{gathered} {\log }_{2}12+\text{\hspace{0.17em}}{\log }_2\frac{1}{3} \\ ={\log }_2\left(12.\frac{1}{3}\right) \\ ={\log }_{2}4=2 \end{gathered}$$

– Chú ý:

Định lí 1 có thể mở rộng cho tích n số dương:

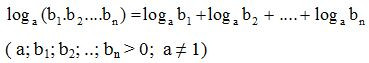
b. Logarit của một thương

– Định lí 2. Cho ba số dương a; b₁ ;b₂ với a ≠ 1. Ta có:

${\log }_a\frac{b_1}{b_2}={\log }_a{b}_1-{\log }_{a}b{}_2$

Logarit của một thương bằng hiệu các logarit.

Đặc biệt: ${\log }_a\frac{1}{b}=-{\log }_{a}b$( a > 0; b > 0; a ≠ 1)

– Ví dụ.

$$\begin{gathered} \log {}_{5}75-{\log }_{5}3 \\ ={\log }_5\frac{75}{3} \\ ={\log }_{5}25=2 \end{gathered}$$

c. Logarit của một lũy thừa

– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:

${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b$

Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.

– Đặc biệt: ${\log }_a\sqrt[n]{b}=\frac{1}{n}{\log }_{a}b$

– Ví dụ .

$\begin{array}{l}\log {}_7{3}^6=6{\log }_{7}3\\ {\log }_3\sqrt[5]{4}=\frac{1}{5}{\log }_{3}4\end{array}$

d. Đổi cơ số

– Định lí 4. Cho ba số dương a; b; c với a ≠ 1; c ≠ 1, ta có:

${\log }_{a}b=\frac{{\log }_{c}b}{{\log }_{c}a}$

– Đặc biệt:

$\begin{array}{l}{\log }_{a}b=\frac{1}{{\log }_{b}a}(\text{}b\ne 1)\\ {\log }_{a^{\alpha }}b=\frac{1}{\alpha }{\log }_{a}b(\alpha \ne 0)\end{array}$

Ví dụ. Tính giá trị các biểu thức sau:

a) $5^{{\log }_{\frac{1}{125}}8}$

b) ${\log }_{2}3.{\log }_{3}4.\mathrm{....}{\log }_{7}8$

Lời giải:

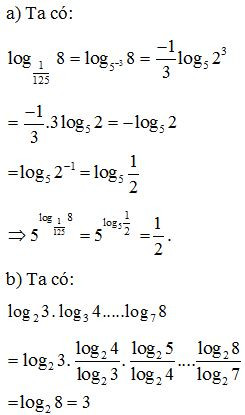
3. Logarit thập phân. Logarit tự nhiên.

a. Logarit thập phân

Logarit thập phân là logarit cơ số 10.

log₁₀b thường được viết là logb hoặc lgb.

b. Logarit tự nhiên

 – Logarit tự nhiên là logarit cơ số e.

log_eb được viết là lnb.

4. Các dạng bài tập về Lôgarit

Dạng 1. Tính giá trị của biểu thức không có điều kiện. Rút gọn biểu thức.

Dạng 2. Đẳng thức chứa logarit.

Dạng 3. Biểu thị biểu thức theo một biểu thức đã cho và từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất (GTLN – GTNN)

II. Ví dụ minh họa

Ví dụ 1.

a) log₃ 27 = 3 vì 3³ = 27.

b) $\log {}_4\left(\frac{1}{16}\right)=-2$ vì $4^{-2}=\frac{1}{16}$.

– Chú ý: Không có logarit của số âm và số 0.

Ví dụ 2.

$4^{-2{\log }_{4}3}={\left(4^{{\log }_{4}3}\right)}^{-2}$$=3^{-2}=\frac{1}{9}$

$\log {}_3\left(\frac{1}{27}\right)$$={\log }_3\left(3^{-3}\right)=-3$

III. Bài tập vận dụng

Bài 1: 

Lời giải:

Bài 2: Đặt a = log₂3, b = log₃5. Hãy tính biểu thức P = log₆60 theo a và b

Lời giải:

Bài 3: Tính giá trị của biểu thức log₃100 - log₃18 - log₃50

Lời giải:

log₃100 - log₃18 - log₃50

Bài 4: Tính giá trị của biểu thức (log₂3)(log₉4)

Lời giải:

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

60 Bài tập về Hàm số lũy thừa (có đáp án năm 2024)

60 Bài tập về Lôgarit (có đáp án năm 2024)

60 Bài tập về Bất phương trình mũ và bất phương trình logarit (có đáp án năm 2024)

60 Bài tập về Nguyên hàm ( có đáp án năm 2024 )

60 Bài tập về Hàm số mũ, Hàm số logarit (2024) có đáp án