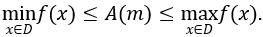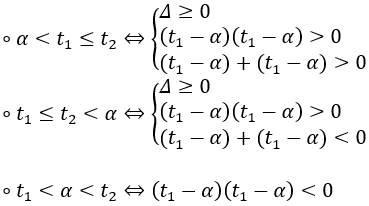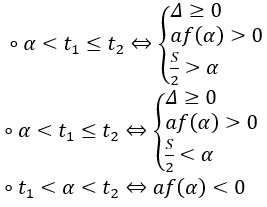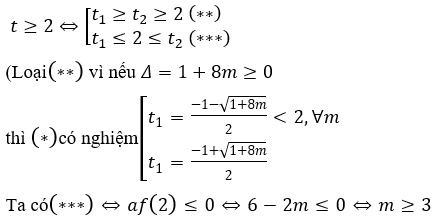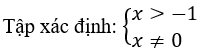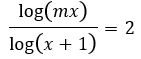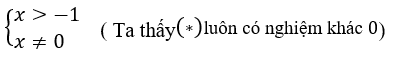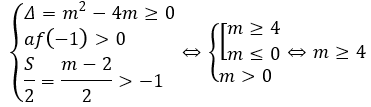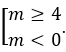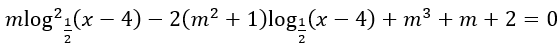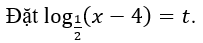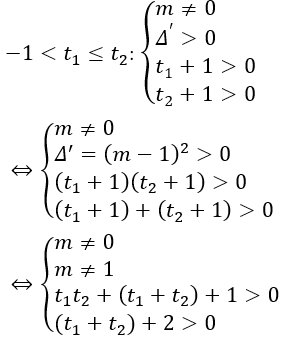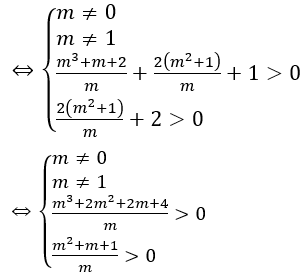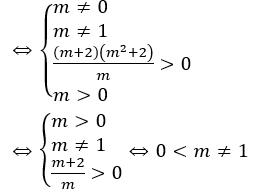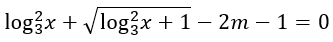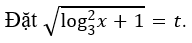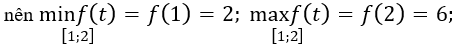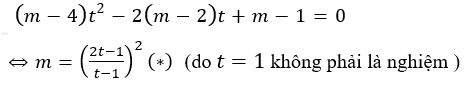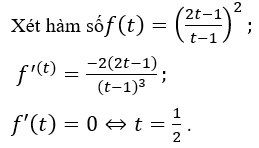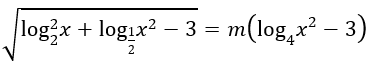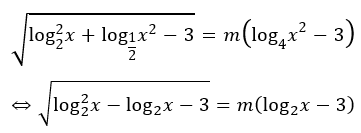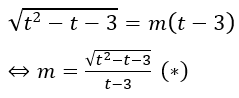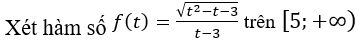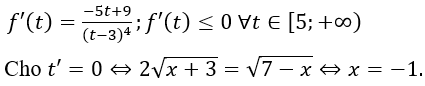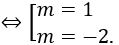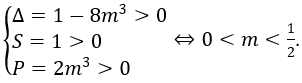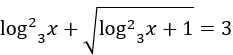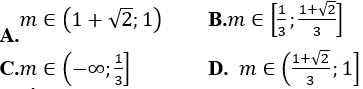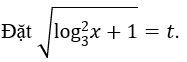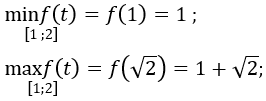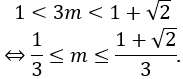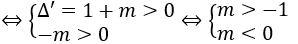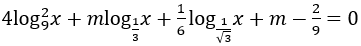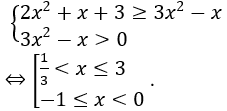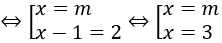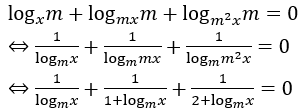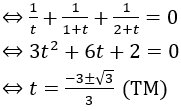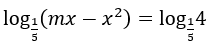20 Bài tập về Giải phương trình logarit chứa tham số (2024) có đáp án

Cách giải phương trình logarit chứa tham số

1. Phương pháp giải

♦ Dạng toán: Tìm m để phương trình có số nghiệm cho trước:

    • Bước 1. Tách m ra khỏi biến số x và đưa về dạng f(x)=A(m).

    • Bước 2. Khảo sát sự biến thiên của hàm số f(x) trên D.

    • Bước 3. Dựa vào bảng biến thiên để xác định giá trị tham số A(m) để đường thẳng y=A(m) nằm ngang cắt đồ thị hàm số y=f(x).

    • Bước 4. Kết luận các giá trị của A(m) để phương trình f(x)=A(m) có nghiệm (hoặc có k nghiệm) trên D.

♦ Lưu ý

    • Nếu hàm số y=f(x) có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị A(m) cần tìm là những m thỏa mãn:

    • Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến thiên để xác định sao cho đường thẳng y=A(m) nằm ngang cắt đồ thị hàm số y=f(x) tại k điểm phân biệt.

Hoặc sử dụng điều kiện có nghiệm của phương trình bậc hai với lưu ý sau.

♦ Nhắc lại: Phương trình bậc hai có hai nghiệm thỏa mãn

Hoặc sử dụng định lí đảo về dấu tam thức bậc hai:

2. Ví dụ minh họa

Ví dụ 1: Tìm tham số thực m để phương trình: log²₃ x + log₃x + m = 0 có nghiệm.

Lời giải:

Tập xác định D=(0;+∞).

Đặt log₃x=t. Khi đó phương trình trở thành t²+t+m=0 (*)

Phương trình đã cho có nghiệm khi phương trình (*) có nghiệm: Δ=1-4m ≥ 0 ⇔ m ≤ 1/4.

Vậy để phương trình có nghiệm thực thì: m ≤ 1/4.

Ví dụ 2: Tìm tham số m để phương trình log₂(5^x-1)log₄(2.5^x-2) = m có nghiệm thực x ≥ 1.

Lời giải:

Điều kiện: 5^x-1 > 0 ⇔ x > 0

log₂(5^x-1)log₄(2.5^x-2) = m

⇔ log₂(5^x-1) 1/2 log₂(2(5^x-1)) = m

⇔ log₂(5^x-1)(1+log₂(5^x-1)) = 2m

⇔ log²₂ (5^x-1)+log₂(5^x-1) = 2m

Đặt log₂(5^x-1)=t. Khi đó phương trình đã cho trở thành t² + t - 2m = 0    (*)

Phương trình đã cho có nghiệm x ≥ 1 khi phương trình (*)có nghiệm

Vậy phương trình có nghiệm thực x ≥ 1 thì m ≥ 3.

Ví dụ 3: Tìm tham số thực m để phương trình 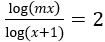 có nghiệm thực duy nhất.

Lời giải:

⇔ log(mx)=2log(x+1)

⇔ log(mx)=log(x+1)²

⇔ mx=(x+1)² ⇔ x²+(2-m)x+1=0 (*)

Phương trình đã cho có nghiệm duy nhất khi phương trình (*)có một nghiệm thỏa mãn

TH1: phương trình (*) có hai nghiệm thỏa mãn -1 < x₁ ≤ x₂:

TH2: phương trình (*) có hai nghiệm thỏa mãn x₁ < -1 < x₂: af(-1) < 0 ⇔ m < 0.

Các giá trị m cần tìm 

3. Bài tập vận dụng (có đáp án)

3.1. Bài tập tự luận

Bài 1: Tìm tham số thực m để phương trình sau có hai nghiệm thực phân biệt trong khoảng (4;6).

Lời giải:

Khi đó phương trình đã cho trở thành: mt²-2(m²+1)t+m³+m+2 = 0 (*).

Yêu cầu bài toán tương đương với (*) phải có hai nghiệm phân biệt

Vậy 0 < m ≠ 1 thỏa yêu cầu bài toán.

Bài 2: Tìm m để phương trình sau có ít nhất một nghiệm trong đoạn[1;3^√3 ] .

Lời giải:

Điều kiện: x > 0.

Khi đó phương trình đã cho trở thành: t²+t-2m-2 = 0 ⇔ t²+t=2m+2 (*).

Yêu cầu bài toán tương đương với (*) phải có ít nhất một nghiệm thuộc đoạn [1;2].

Xét hàm số f(t)=t²+t trên đoạn[1;2] . Ta có f'(t) = 2t+1 > 0, ∀t ∈ [1;2]

Để (*) có ít nhất một nghiệm thuộc đoạn [1;2] thì 2 < 2m+2 < 6 ⇔ 0 < m < 2

Bài 3: Tìm tham số m để (m-4)log₂² x-2(m-2)log₂ x+m-1=0 có hai nghiệm thỏa 1 < x₁ < 2 < x₂

Lời giải:

Đặt log₂ x=t, phương trình đã cho trở thành:

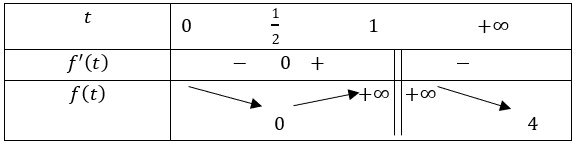
Yêu cầu bài toán tương đương với (*) phải có hai nghiệm thỏa mãn 0 < t₁ < 1 < t₂.

Từ BBT ⇒ m > 4.

Bài 4: Tìm tham số m để phương trình sau có nghiệm thực thuộc [32;+∞].

Lời giải:

Đặt log₂ x=t, phương trình đã cho trở thành:

Yêu cầu bài toán tương đương với (*) phải có hai nghiệm phân biệt t ≥ 5:

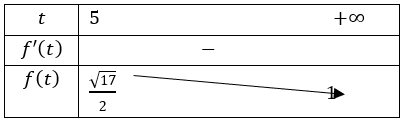
Bảng biến thiên

Căn cứ BBT suy ra giá trị cần tìm là m ∈ (1;√17/2].

Bài 5: Tìm tất cả các giá trị thực của tham số m để phương trình log₂ (mx-x² )=2 vô nghiệm?

Lời giải:

log₂ mx-x² = 2 ⇔ -x²+mx-4 = 0 (*)

Phương trình (*) vô nghiệm ⇔ Δ < 0 ⇔ m²-16 < 0 ⇔ -4 < m < 4

Bài 6: Tìm tất cả các giá trị thực của tham số m để phương trình log₄² x+3log₄ x+2m-1=0 có 2 nghiệm phân biệt?

Lời giải:

Phương trình có 2 nghiệm phân biệt ⇔ Δ > 0 ⇔ 13-8m > 0 ⇔ m < 13/8

3.2. Bài tập trắc nghiệm

Bài 1: Với giá trị m bằng bao nhiêu thì phương trình log_(2+√3) (mx+3)+log_2-√3 (m²+1)=0 có nghiệm là -1?

Lời giải:

Đáp án :

Giải thích :

Thay x=-1 vào phương trình ta có

log_(2+√3) (-m+3)+log_2-√3(m²+1)=0 ⇔ log_(2+√3) (-m+3)+log_(2+√3)^-1 (m²+1)=0

⇔ log_(2+√3) (-m+3)-log_2+√3(m²+1)=0

⇔ log_(2+√3) (-m+3)=log_2+√3(m²+1)

⇔ -m+3=m²+1 ⇔ m²+m-2=0 < 

Bài 2: Với giá trị nào của m thì phương trình log₂ (4^x+2m³)=x có hai nghiệm phân biệt?

Lời giải:

Đáp án :

Giải thích :

log₂ (4^x+2m³)=x ⇔ 4^x+2m³=2^x ⇔ 4^x-2^x+2m³=0

Đặt 2^x=t (t > 0). Khi đó phương trình trở thành t²-t+2m³=0 (*)

Phương trình đã cho có hai nghiệm phân biệt khi phương trình (*) có hai nghiệm dương phân biệt :

Vậy để phương trình có nghiệm thực thì: 0 < m < 1/2.

Bài 3: Với giá trị nào của m thì phương trình sau có nghiệm trên 1;3 .

Lời giải:

Đáp án :

Giải thích :

Điều kiện: x > 0.

Khi đó phương trình đã cho trở thành: t²+t-1=3m (*) .

Yêu cầu bài toán tương đương với (*) phải có nghiệm thuộc đoạn [1;√2].

Xét hàm số f(t)=t²+t-1 trên đoạn [1;√2]. Ta có f'(t) =2t+1 > 0, ∀ t ∈ [1 ;√2]

Để (*) có nghiệm thuộc đoạn [1;√2] thì

Bài 4: Tìm m để phương trình log₂ (x³-3x)=m có ba nghiệm thực phân biệt.

A. m < 1.        B.0< m < 1        C. m > 0.        D. m > 1.

Lời giải:

Đáp án :

Giải thích :

PT ⇔ x³-3x=2^m < 1

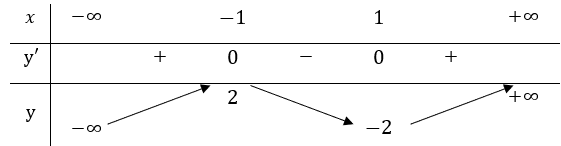
f(x)=x³-3x; f'(x)=3x²-3; f'(x)=0 ⇔ x=±1

BBT

Phương trình có ba nghiệm phân biệt khi và chỉ khi -2 < 2^m < 2 ⇔ m < 1

• Trắc nghiệm PT ⇔ x³-3x=2^m ⇔ x³-3x-2^m=0

Bấm máy tính giải phương trình bậc 3:

Thay m=0,5. Giải pt x³-3x-2^0,5=0 có ba nghiệm phân biệt. Loại D

Thay m=-1. Giải pt x³-3x-2^-1=0 có ba nghiệm phân biệt. Chọn A.

Bài 5: Tìm m để phương trình log₂ (4^x-m)=x+1 có đúng hai nghiệm phân biệt.

A. 0< m < 1        B. 0< m < 2        C. -1< m < 0.        D. -2< m < 0.

Lời giải:

Đáp án :

Giải thích :

• Tự luận: PT ⇔ 4^x-m=2^x+1 ⇔ 2²x-2.2^x-m=0

Đặt ẩn phụ t=2^x, t > 0. Yêu cầu bài toán tương đương pt t²-2t-m=0 có hai nghiệm dương phân biệt

• Trắc nghiệm PT ⇔ 4^x-m=2^x+1 ⇔ 2²x-2.2^x-m=0

Đặt ẩn phụ t=2^x,t > 0. Yêu cầu bài toán tương đương pt t²-2t-m=0 có hai nghiệm dương phân biệt .

Thấy pt có hai nghiệm dương thì a.c > 0⇒-m > 0⇒m < 0. Nên loại A,B

Thử m=-1,5 thấy phương trình t²-2t+1,5=0 vô nghiệm. Nên loại D, chọn C.

Bài 6: Cho phương trình sau với m là tham số. Tìm m để phương trình có hai nghiệm x₁,x₂ thỏa mãn x₁ x₂=3. Mệnh đề nào sau đây đúng?

A. 1< m < 2.        B.3< m < 4.        C. 0< m < 3/2.        D. 2< m < 3.

Lời giải:

Đáp án :

Giải thích :

PT được viết lại: 9log₃² x-(9m+3)log₃ x+9m-2=0 .

Nếu đặt t=log₃ x ,khi đó ta tìm

(Chú ý trong các trường hợp tổng quát cần điều kiện có nghiệm của phương trình bậc 2).

Bài 7: Với m là tham số thực dương khác 1. Hãy tìm tập nghiệm S của bất phương trình log_m (2x²+x+3) ≤ log_m (3x²-x). Biết rằng x = 1 là một nghiệm của bất phương trình.

Lời giải:

Đáp án :

Giải thích :

x=1 là nghiệm nên log_m 6 ≤ log_m 2 ⇔ 0< m < 1 . Khi đó ta có BPT:

Bài 8: Tìm tất cả các giá trị của m để phương trình x.log₂ (x-1)+m=m.log₂ (x-1)+x có hai nghiệm thực phân biệt thuộc (1;3] .

A. m > 3.        B. 1< m < 3.        C. m ≠ 3.        D. Không có m.

Lời giải:

Đáp án :

Giải thích :

ĐK: x > 1

x.log₂ (x-1)+m=m.log₂ (x-1)+x ⇔ (x-m)log₂ (x-1)=x-m <

⇔ (x-m)(log₂ (x-1) - 1) = 0

Phương trình có hai nghiệm phân biệt thuộc (1;3] khi 1< x=m < 3.

Bài 9: Tìm tất cả các giá trị của tham số m để phương trình log₃² x-(m+2).log₃ x+3m-1=0 có 2 nghiệm x₁,x₂ sao cho x₁ x₂=27.

A. m=4/3.        B.m=25.        C.m=28/3.        D.m=1.

Lời giải:

Đáp án :

Giải thích :

Nếu đặt t=log₃ x, khi đó ta tìm t₁+t₂=log₃ x₁+log₃ x₂=log₃ x₁.x₂=3 ⇔ m+2=3 ⇔ m=1.

Bài 10: Định điều kiện cho tham số m để: log_x m+log_mx m+log_m² x m=0 có nghiệm .

Lời giải:

Đáp án :

Giải thích :

ĐK: m > 0.

Với m=1. Phương trình: log_x 1=0 nghiệm đúng mọi 0 < x ≠ 1 .

Với 0 < m ≠ 1. Phương trình:

Đặt log_m x=t (t ≠ 0; t ≠ -1; t ≠ 2).

Khi đó có phương trình:

Vậy m > 0.

Bài 11: Tìm tất cả các giá trị thực của tham số mđể phương trình log₃ x-log₃ (x-2)=log_√3 m có nghiệm?

A. m > 1.        B. m ≥ 1.        C. m < 1.        D. m ≤ 1.

Lời giải:

Đáp án :

Giải thích :

[Phương pháp tự luận]

Điều kiện x > 2; m > 0

Phương trình có nghiệm x > 2 khi m > 1,chọn đáp án A

[Phương pháp trắc nghiệm]

Thay m=0 (thuộc C, D) vào biểu thức log_√3 m không xác định, vậy loại C, D

Thay m=1 (thuộc B) ta được phương trình tương đương x=x-2 vô nghiệm

Vậy chọn đáp án A.

Bài 12: Tìm tất cả giá trị thực của tham số m để bất phương trình sau vô nghiệm?

Lời giải:

Đáp án :

Giải thích :

x²-mx+4=0 vô nghiệm ⇔ x²-mx+4 < 0 ∀ x ∈ R ⇔ Δ < 0 ⇔ -4 < m < 4

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

60 Bài tập về Hàm số lũy thừa (có đáp án năm 2023)

60 Bài tập về Lôgarit (có đáp án năm 2023)

60 Bài tập về Bất phương trình mũ và bất phương trình logarit (có đáp án năm 2023)

60 Bài tập về Nguyên hàm ( có đáp án năm 2023 )

60 Bài tập về Hàm số mũ, Hàm số logarit (2024) có đáp án