10 câu hỏi trắc nghiệm thuộc Dạng 4. Áp dụng các trường hợp đồng dạng của tam giác vào vấn đề thực tiễn

Trắc nghiệm Toán 8 Bài 34. Ba trường hợp đồng dạng của hai tam giác có đáp án

Dạng 4. Áp dụng các trường hợp đồng dạng của tam giác vào vấn đề thực tiễn

221 lượt thi
10 câu hỏi
0 phút

Danh sách câu hỏi

Câu 1:

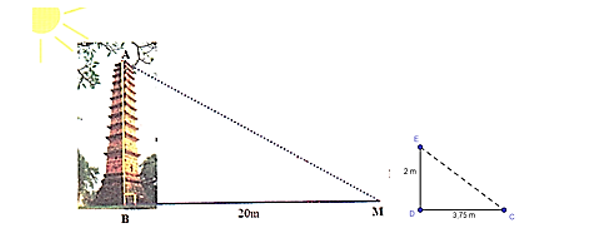
Bóng của Tháp Bình Sơn trên mặt đất có độ dài 20 m. Cùng thời điểm đó, một cột sắt cao 2 m cắm vuông góc với mặt đất có bóng dài 3,75 m. Biết các chùm ánh sáng là song song với nhau. Chiều cao của Tháp Bình Sơn (làm tròn đến hàng phần mười) là

Bóng của Tháp Bình Sơn trên mặt đất có độ dài 20 m. Cùng thời điểm đó, một cột sắt cao 2 m cắm vuông (ảnh 1)

A. 10,7 m;

B. 10,6 m;

C. 10,67 m;

D. 10,66 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Xét hai tam giác ABM và EDC có:

$\hat{AMB} = \hat{ECD}$ (AM // EC, hai góc đồng vị)

$\hat{ABM} = \hat{EDC} = 90 °$

Do đó, ΔABM ᔕ ΔEDC (g – g).

Suy ra $\frac{AB}{ED} = \frac{BM}{DC}$ hay $\frac{AB}{2} = \frac{20}{3, 75}$ .

Suy ra $AB = \frac{2 \cdot 20}{3, 75} \approx 10, 7$ (m).

Câu 2:

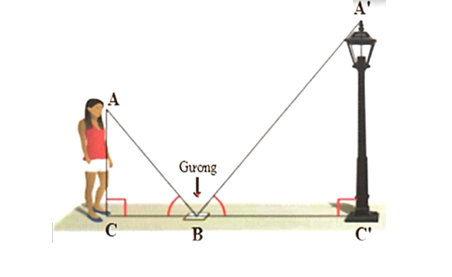
Trong hình vẽ bên, độ rộng của khúc sông được tính bằng khoảng cách giữa hai vị trí B và C. Chọn các vị trí A, C', B' sao cho hai tam giác ABC và AB'C' đồng dạng. Tính độ rộng khúc sông (làm tròn đến hàng phần mười), biết AC = 120 m, AC' = 52 m, B'C' = 20 m

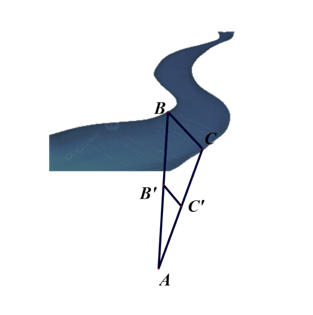
Trong hình vẽ bên, độ rộng của khúc sông được tính bằng khoảng cách giữa hai vị trí B và C. Chọn các vị trí (ảnh 1)

A. 46,15 m;

B. 46 m;

C. 46,1 m;

D. 46,2 m

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Vì ΔABC ᔕ ΔAB'C' nên $\frac{AC}{AC'} = \frac{BC}{B'C'}$ hay $\frac{120}{52} = \frac{BC}{20}$ .

Suy ra $BC = \frac{120 \cdot 20}{52} \approx 46, 2$ (m).

Câu 3:

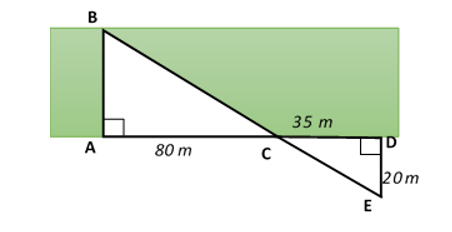
Một cột đèn cao 7 m có bóng trên mặt đất dài 4 m. Gần đấy có một tòa nhà cao tầng có bóng trên mặt đất là 80 m (như hình vẽ). Em hãy cho biết tòa nhà có bao nhiêu tầng biết rằng mỗi tầng cao 3,5 m.

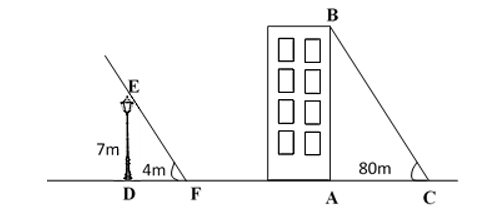
Một cột đèn cao 7 m có bóng trên mặt đất dài 4 m. Gần đấy có một tòa nhà cao tầng có bóng trên mặt đất là (ảnh 1)

A. 27 tầng;

B. 35 tầng;

C. 40 tầng;

D. 42 tầng.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Xét hai tam giác DEF và ABC có:

$\hat{DFE} = \hat{ACB}$

$\hat{EDF} = \hat{BAC} = 90 °$

Do đó, ΔDEF ᔕ ΔABC (g – g).

Suy ra $\frac{DE}{AB} = \frac{DF}{AC}$ hay $\frac{7}{AB} = \frac{4}{80}$ .

Suy ra $AB = \frac{7 \cdot 80}{4} = 140$ (m)

Vậy tòa nhà cao 140 m.

Số tầng của tòa nhà là: 140 : 3,5 = 40 (tầng).

Câu 4:

Một ngọn đèn đặt trên cao ở vị trí A, hình chiếu vuông góc của nó trên mặt đất là H. Người ta đặt hai chiếc cọc dài 1,6 m thẳng đứng ở hai vị trí B và C thẳng hàng với H, khi đó bóng của mỗi chiếc cọc có độ dài lần lượt là 0,4 m và 0,6 m. Biết BC = 1,4 m, độ cao AH bằng

Một ngọn đèn đặt trên cao ở vị trí A, hình chiếu vuông góc của nó trên mặt đất là H. Người ta đặt hai chiếc (ảnh 1)

A. 3,48 m;

B. 3,84 m;

C. 4,38 m;

D. 4,83 m.

Xem đáp án

Một ngọn đèn đặt trên cao ở vị trí A, hình chiếu vuông góc của nó trên mặt đất là H. Người ta đặt hai chiếc (ảnh 2)

Câu 5:

Một cột cờ AB vuông góc với mặt đất và có bóng là AC dài 12 m. Cùng lúc đó, người ta dựng một cây cọc MN cao 4 m và có bóng trên mặt đất là MQ dài 2,4 m. Biết các chùm ánh sáng là song song với nhau. Khi đó chiều cao của cột cờ

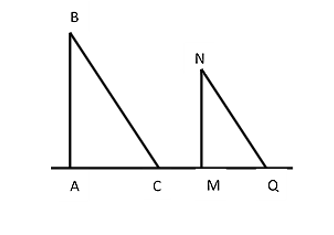
Một cột cờ AB vuông góc với mặt đất và có bóng là AC dài 12 m. Cùng lúc đó, người ta dựng một cây cọc MN (ảnh 1)

A. 12,8 m;

B. 20 m;

C. 7,2 m;

D. 9,6 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Xét hai tam giác ABC và MNQ có:

$\hat{ACB} = \hat{MQN}$ (BC // MN, hai góc đồng vị)

$\hat{BAC} = \hat{NMQ} = 90 °$

Do đó, ΔABC ᔕ ΔMNQ (g – g).

Suy ra $\frac{AB}{MN} = \frac{AC}{MQ}$ hay $\frac{AB}{4} = \frac{12}{2, 4}$ .

Suy ra $AB = \frac{4 \cdot 12}{2, 4} = 20$ (m).

Câu 6:

Một giếng nước có đường kính DE = 0,8 m (hình bên dưới). Để xác định độ sâu BD của giếng, người ta đặt một chiếc gậy ở vị trí AC, A chạm miệng giếng, AC nhìn thẳng tới vị trí E ở góc của đáy giếng. Biết AB = 0,9 m, BC = 0,2 m. Độ sâu BD của giếng là

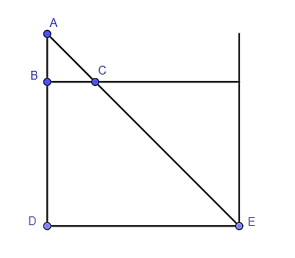
Một giếng nước có đường kính DE = 0,8 m (hình bên dưới). Để xác định độ sâu BD của giếng (ảnh 1)

A. 2,7 m;

B. 3,6 m;

C. 4,2 m;

D. 5,4 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Xét hai tam giác ABC và ADE có:

$\hat{A}$ : Góc chung

$\hat{ABC} = \hat{ADE} = 90 °$

Do đó, ΔABC ᔕ ΔADE (g – g).

Suy ra $\frac{AB}{AD} = \frac{BC}{DE}$ hay $\frac{0, 9}{AD} = \frac{0, 2}{0, 8}$ .

Suy ra $AD = \frac{0, 9 \cdot 0, 8}{0, 2} = 3, 6$ (m).

Mà AD = AB + DB nên DB = AD – AB = 3,6 – 0,9 = 2,7 (m).

Câu 7:

Để đo chiều cao của cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt của người quan sát nhìn thẳng vào tấm gương, người quan sát di chuyển sao cho thấy được đỉnh ngọn đèn trong tấm gương và $\hat{ABC}$ = $\hat{A'BC'}$ . Cho chiều cao tính từ mắt của người quan sát đến mặt đất là AC = 1,7 m, khoảng cách từ gương đến chân người là BC = 0,6 m, khoảng cách từ gương đến chân cột đèn là BC' = 1,5 m. Chiều cao của cột đèn A'C' bằng

Để đo chiều cao của cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt (ảnh 1)

A. 3,4 m;

B. 3,5 m;

C. 4 m;

D. 4,25 m.

Xem đáp án

Để đo chiều cao của cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt (ảnh 2)

Câu 8:

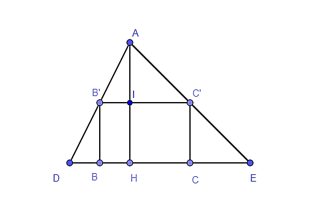
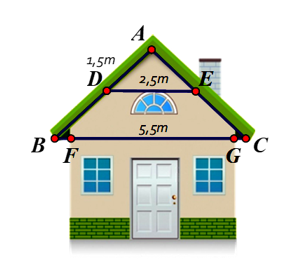
Một ngôi nhà có thiết kế mái như hình bên và có các số đo như sau: AD = 1,5 m, DE = 2,5 m, BF = GC = 1 m, FG = 5,5 m. Tính chiều dài AB của mái nhà bên, biết DE // BC.

Một ngôi nhà có thiết kế mái như hình bên và có các số đo như sau: AD = 1,5 m, DE = 2,5 m, BF = GC = 1 m (ảnh 1)

A. 5,4 m;

B. 4,5 m;

C. 3,3 m;

D. 12,5 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Có BC = BF + FG + GC = 1 + 5,5 + 1 = 7,5 (m).

Xét tam giác ABC, do DE // BC nên ΔABC ᔕ ΔADE.

Suy ra $\frac{AD}{AB} = \frac{DE}{BC}$ hay $\frac{1, 5}{AB} = \frac{2, 5}{7, 5}$ .

Suy ra $AB = \frac{1, 5 \cdot 7, 5}{2, 5} = 4, 5$ (m).

Câu 9:

Cho hình vẽ, biết AC = 80 m; CD = 35 m; DE = 20 m. Chiều rộng AB của khúc sông (làm tròn đến hàng phần mười) là

A. 45,7 m;

B. 45,71 m;

C. 47,5 m;

D. 47 m.

Xem đáp án

Cho hình vẽ, biết AC = 80 m; CD = 35 m; DE = 20 m. Chiều rộng AB của khúc sông (làm tròn đến hàng phần mười) là (ảnh 2)

Câu 10:

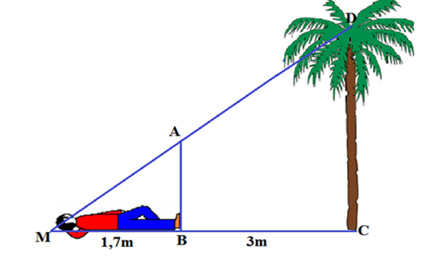
Bạn Hoàng muốn đo chiều cao của một cây dừa mọc thẳng đứng trong sân, bạn dùng một cây cọc AB cao 1,5 m và chiều dài thân mình để đo. Bạn nằm cách gốc cây 3 m (tính từ chân của bạn) và bạn cắm cọc thẳng đứng dưới chân mình thì bạn thấy đỉnh thân cọc và đỉnh cây thẳng hàng với nhau. Em hãy giúp bạn tính chiều cao của cây dừa, biết bạn Hoàng cao 1,7 m (làm tròn kết quả đến hàng phần mười).

Bạn Hoàng muốn đo chiều cao của một cây dừa mọc thẳng đứng trong sân, bạn dùng một cây cọc AB cao 1,5 m và (ảnh 1)

A. 4,8 m;

B. 3,2 m;

C. 4,1 m;

D. 5,4 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Có MC = MB + BC = 1,7 + 3 = 4,7 (m).

Xét hai tam giác MBA và MCD có:

$\hat{M}$ : Góc chung

$\hat{MBA} = \hat{MCD} = 90 °$

Do đó, ΔMBA ᔕ ΔMCD (g – g).

Suy ra $\frac{MB}{MC} = \frac{AB}{DC}$ hay $\frac{1,7}{4, 7} = \frac{1, 5}{DC}$ .

Suy ra $DC = \frac{4, 7 \cdot 1, 5}{1, 7} \approx 4, 1$ (m).

Bắt đầu thi ngay

Trắc nghiệm Toán 8 Bài 34. Ba trường hợp đồng dạng của hai tam giác có đáp án

Dạng 4. Áp dụng các trường hợp đồng dạng của tam giác vào vấn đề thực tiễn

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương