10 câu hỏi trắc nghiệm thuộc Dạng 2.Trường hợp đồng dạng thứ hai của tam giác

Trắc nghiệm Toán 8 Bài 34. Ba trường hợp đồng dạng của hai tam giác có đáp án

Dạng 2.Trường hợp đồng dạng thứ hai của tam giác

206 lượt thi
10 câu hỏi
0 phút

Danh sách câu hỏi

Câu 1:

Cho góc xOy khác góc bẹt. Trên Ox lấy các điểm A và C, trên Oy lấy các điểm B và D sao cho OA ⋅ OD = OB ⋅ OC. Khẳng định nào sau đây là đúng?

A. ΔAOB ᔕ ΔCOD;

B. ΔABO ᔕ ΔCOD;

C. ΔBAO ᔕ ΔOCD;

D. ΔOBA ᔕ ΔDCO.

Xem đáp án

Hướng dẫn giải:

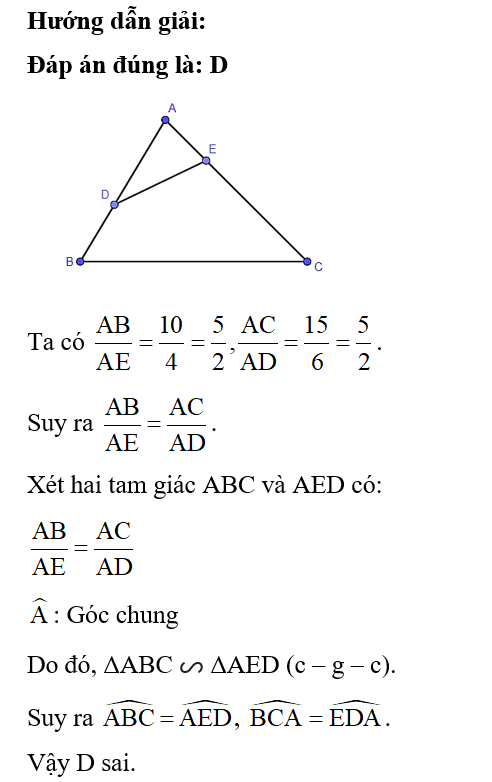
Đáp án đúng là: A

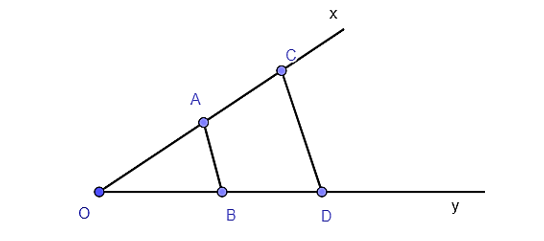
Cho góc xOy khác góc bẹt. Trên Ox lấy các điểm A và C, trên Oy lấy các điểm B và D (ảnh 1)

Vì OA ⋅ OD = OB ⋅ OC nên $\frac{AO}{CO} = \frac{BO}{DO}$ .

Xét hai tam giác AOB và COD có:

$\frac{AO}{CO} = \frac{BO}{DO}$

$\hat{O}$ : Góc chung

Suy ra ΔAOB ᔕ ΔCOD (c – g – c).

Câu 2:

Cho hình thang ABCD (AB // CD), biết AB = 9 cm, BD = 12 cm, DC =16 cm. Tam giác BDC đồng dạng với tam giác nào dưới đây?

A. Tam giác ACD;

B. Tam giác ABC;

C. Tam giác ABD;

D. Cả A, B, C đều sai.

Xem đáp án

Hướng dẫn giải:

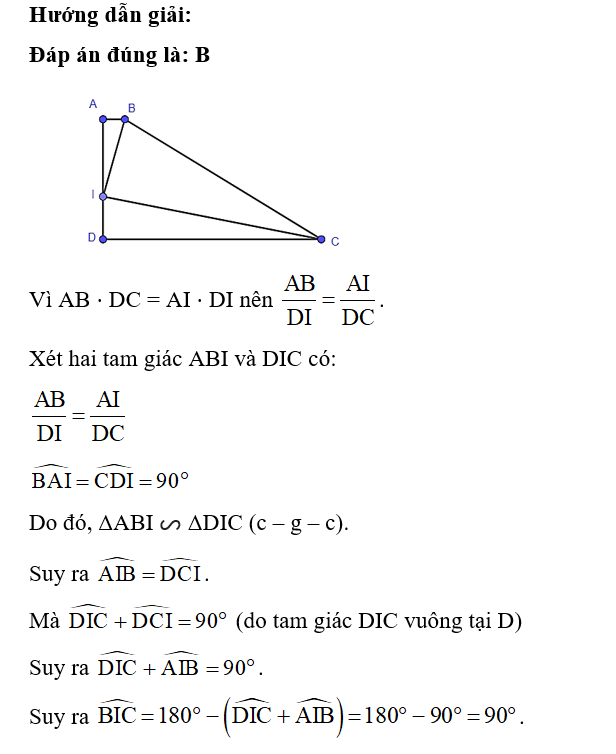
Đáp án đúng là: C

Vì AB // CD nên $\hat{ABD} = \hat{CDB}$ (so le trong).

Ta có $\frac{AB}{BD} = \frac{9}{12} = \frac{3}{4}, \frac{BD}{DC} = \frac{12}{16} = \frac{3}{4}$ .

Suy ra $\frac{AB}{BD} = \frac{BD}{DC}$ .

Xét hai tam giác BDC và ABD có:

$\hat{ABD} = \hat{CDB}$

$\frac{AB}{BD} = \frac{BD}{DC}$

Suy ra ΔBDC ᔕ ΔABD (c – g – c).

Câu 3:

Cho tam giác ABC có AB = 10 cm, AC = 15 cm. Trên cạnh AB lấy D sao cho AD = 6 cm, trên cạnh AC lấy điểm E sao cho AE = 4 cm. Khẳng định nào sau đây là sai?

A. ΔABC ᔕ ΔAED;

B. $\hat{ABC} = \hat{AED}$ ;

C. $\hat{BCA} = \hat{EDA}$ ;

\hat{AED} = \hat{ACB}

Xem đáp án

Cho tam giác ABC có AB = 10 cm, AC = 15 cm. Trên cạnh AB lấy D sao cho AD = 6 cm, trên (ảnh 1)

Câu 4:

Cho hình thang vuông ABCD vuông tại A và D. Trên cạnh AD lấy I sao cho AB ⋅ DC = AI ⋅ DI. Khi đó $\hat{BIC}$ bằng

A. 120°;

B. 90°;

C. 30°;

D. 75°.

Xem đáp án

Cho hình thang vuông ABCD vuông tại A và D. Trên cạnh AD lấy I sao cho AB ⋅ DC = AI ⋅ DI. Khi đó (ảnh 1)

Câu 5:

Điền vào chỗ chấm. Cho hình thoi MNPQ có $\hat{M} = 60 °$ . Qua P kẻ đường thẳng d bất kì cắt các tia đối của các tia NM, QM theo thứ tự tại E và F. Khi đó tam giác NQF đồng dạng với tam giác ……

A. MNQ;

B. ENQ;

C. MPF;

D. NEP.

Xem đáp án

Điền vào chỗ chấm. Cho hình thoi MNPQ có góc M= 60 độ . Qua P kẻ đường thẳng d bất kì cắt các tia (ảnh 1)

Điền vào chỗ chấm. Cho hình thoi MNPQ có góc M= 60 độ . Qua P kẻ đường thẳng d bất kì cắt các tia (ảnh 2)

Câu 6:

Cho tam giác MNP có MN = 12 cm, MP = 15 cm, NP = 18 cm. Trên các cạnh MN, MP lần lượt lấy R, S sao cho MR = 10 cm và MS = 8 cm. Độ dài đoạn thẳng RS là

A. 12 cm;

B. 15 cm;

C. 14,2 cm;

D. 16,1 cm.

Xem đáp án

Cho tam giác MNP có MN = 12 cm, MP = 15 cm, NP = 18 cm. Trên các cạnh MN, MP lần lượt lấy (ảnh 1)

Câu 7:

Cho tam giác ABC có AB = 9 cm, AC = 12 cm, BC = 7 cm. Khẳng định nào sau đây là đúng?

A. $\hat{C} = 3 \hat{B}$ ;

B. $\hat{C} = \frac{1}{3} \hat{B}$ ;

C. $\hat{C} = \frac{1}{2} \hat{B}$ ;

\hat{C} = 2 \hat{B}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

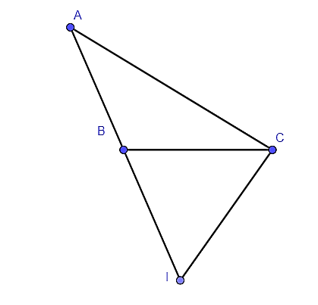
Cho tam giác ABC có AB = 9 cm, AC = 12 cm, BC = 7 cm. Khẳng định nào sau đây là đúng? (ảnh 1)

Trên tia đối của tia BA lấy điểm I sao cho BI = BC = 7 cm.

Suy ra AI = AB + BI = 9 + 7 = 16 (cm).

Ta có $\frac{AB}{AC} = \frac{9}{12} = \frac{3}{4}, \frac{AC}{AI} = \frac{12}{16} = \frac{3}{4}$ .

Suy ra $\frac{AB}{AC} = \frac{AC}{AI}$ .

Xét hai tam giác ABC và ACI có:

$\hat{A}$ : Góc chung

$\frac{AB}{AC} = \frac{AC}{AI}$

Do đó, ΔABC ᔕ ΔACI (c – g – c).

Suy ra $\hat{BCA} = \hat{I}$ .

Mà $\hat{ABC} = \hat{I} + \hat{BCI}$ (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó).

Và $\hat{I} = \hat{BCI}$ (tam giác BCI cân tại B).

Suy ra $\hat{ABC} = 2 \hat{I} = 2 \hat{BCA}$ hay $\hat{C} = \frac{1}{2} \hat{B}$ .

Câu 8:

Cho tam giác MNP có MN = 18 cm, MP = 27 cm, NP = 30 cm. Gọi D là trung điểm của MN, E thuộc MP sao cho ME = 6 cm. Độ dài DE bằng

A. 8 cm;

B. 12 cm;

C. 9 cm;

D. 10 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

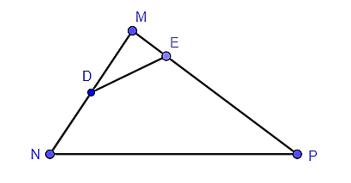
Cho tam giác MNP có MN = 18 cm, MP = 27 cm, NP = 30 cm. Gọi D là trung điểm của MN, E thuộc (ảnh 1)

Vì D là trung điểm của MN nên MD = $\frac{1}{2}$ MN = 9 cm.

Ta có $\frac{ME}{MN} = \frac{6}{18} = \frac{1}{3}, \frac{MD}{MP} = \frac{9}{27} = \frac{1}{3}$ .

Suy ra $\frac{ME}{MN} = \frac{MD}{MP}$ .

Xét hai tam giác MED và MNP có:

$\hat{M}$ : Góc chung

$\frac{ME}{MN} = \frac{MD}{MP}$

Do đó, ΔMED ᔕ ΔMNP (c – g – c).

Suy ra $\frac{DE}{PN} = \frac{MD}{MP} = \frac{1}{3}$ hay $\frac{DE}{30} = \frac{1}{3}$ .

Suy ra DE = 10 (cm).

Câu 9:

Cho hình thang ABCD (AB // CD), $\hat{A} = \hat{D} = 90 °$ , AB = 2 cm, CD = 4,5 cm, BD = 3 cm. Khi đó BC vuông góc với

A. BD;

B. AD;

C. AC;

D. DC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

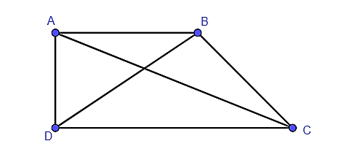
Cho hình thang ABCD (AB song song CD), góc A = góc D= 90 độ, AB = 2 cm, CD = 4,5 cm (ảnh 1)

Ta có $\frac{AB}{BD} = \frac{2}{3}, \frac{BD}{DC} = \frac{3}{4, 5} = \frac{2}{3}$ .

Suy ra $\frac{AB}{BD} = \frac{BD}{DC}$ .

Xét hai tam giác BAD và DBC có:

$\hat{ABD} = \hat{BDC}$ (AB // CD, hai góc so le trong)

$\frac{AB}{BD} = \frac{BD}{DC}$

Khi đó, ΔBAD ᔕ ΔDBC (c – g – c).

Suy ra $\hat{DBC} = \hat{B A D} = 90 °$ .

Do đó, DB ⊥ BC.

Câu 10:

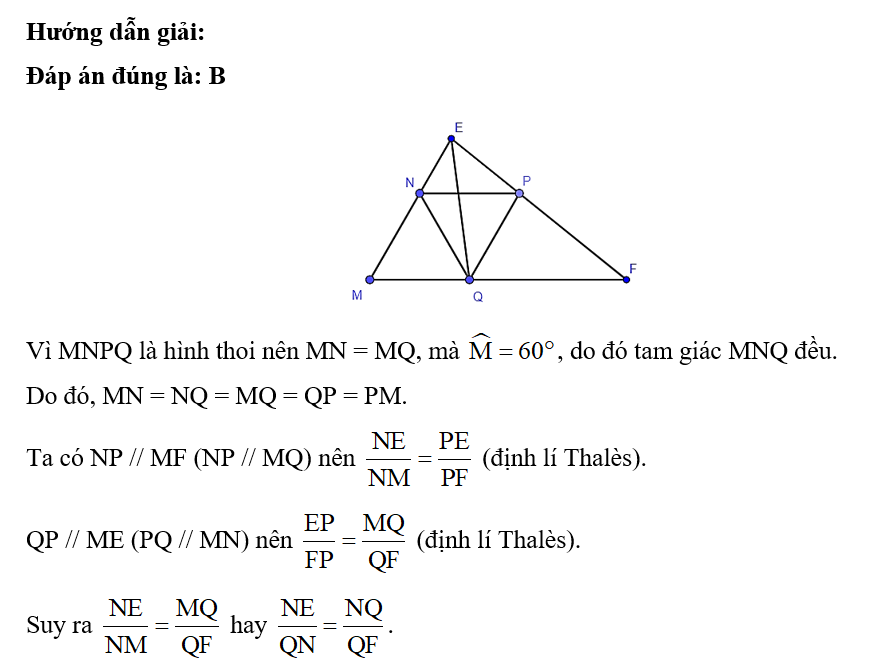
Cho hình bình hành ABCD, kẻ AH ⊥ CD tại H, AK ⊥ BC tại K. Tam giác KAH đồng dạng với tam giác nào dưới đây?

A. Tam giác ACK;

B. Tam giác ABH;

C. Tam giác ABC;

D. Tam giác AHC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

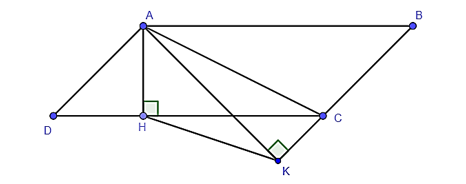
Cho hình bình hành ABCD, kẻ AH ⊥ CD tại H, AK ⊥ BC tại K. Tam giác KAH đồng dạng với tam giác nào dưới đây? (ảnh 1)

Ta có S_ABCD = AH ⋅ DC = AK ⋅ BC.

Mà DC = AB (ABCD là hình bình hành).

Do đó, AH ⋅ AB = AK ⋅ BC.

Suy ra $\frac{AB}{AK} = \frac{BC}{AH}$ .

Xét hai tam giác ABC và KAH có:

$\frac{AB}{AK} = \frac{BC}{AH}$

$\hat{B} = \hat{KAH}$ (cùng phụ với $\hat{BAK}$ ).

Suy ra ΔABC ᔕ ΔKAH (c – g – c).

Bắt đầu thi ngay

Trắc nghiệm Toán 8 Bài 34. Ba trường hợp đồng dạng của hai tam giác có đáp án

Dạng 2.Trường hợp đồng dạng thứ hai của tam giác

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương