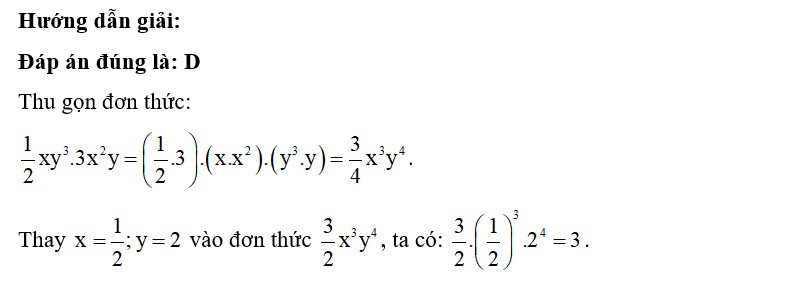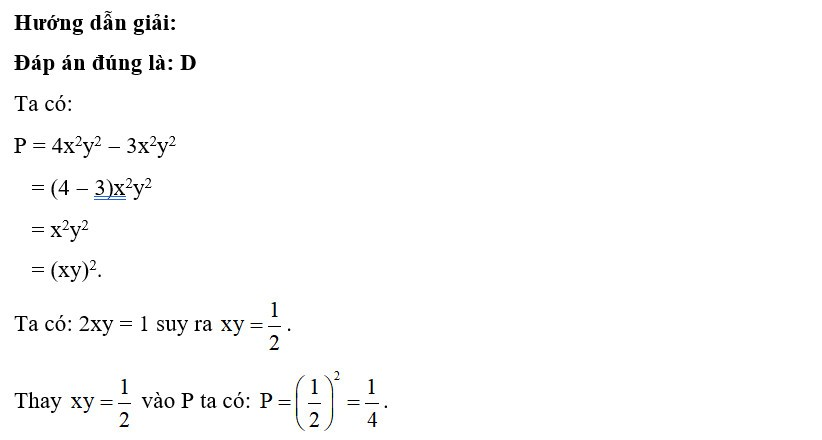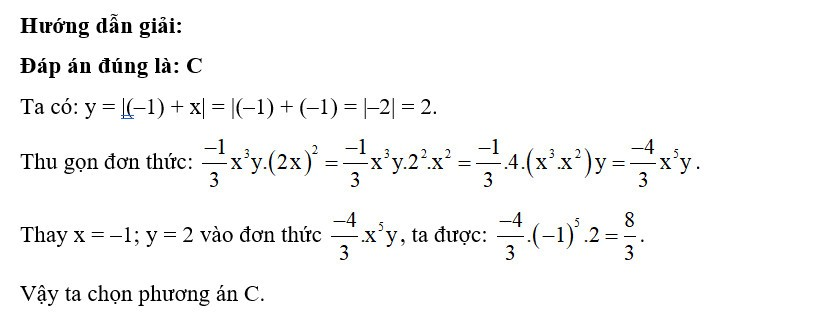10 câu hỏi trắc nghiệm thuộc Dạng 4: Tìm giá trị đơn thức khi biết giá trị của biến

Trắc nghiệm Toán 8 Bài 1. Đơn thức

Dạng 4: Tìm giá trị đơn thức khi biết giá trị của biến

236 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giá trị đơn thức 2xy³ tại x = 2; y = 1 là

A. 8;

B. 2;

C. 4;

D. 6.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Thay x = 2; y = 1 vào đơn thức 2xy³, ta có: 2.2.1³ = 4.

Câu 2:

Giá trị đơn thức $\frac{1}{2} x^{3} y^{2}$ tại x = 0,5; y = 1 là:

A. $\frac{1}{15};$

B. $\frac{1}{16}$ ;

C. $\frac{1}{8}$ ;

D. $\frac{1}{10}$ .

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Thay x = 0,5; y = 1 vào đơn thức $\frac{1}{2} x^{3} y^{2}$ , ta có: $\frac{1}{2} . 0, 5^{3} . 1^{2} = \frac{1}{2} . 0, 5^{3} . 1^{2} = \frac{1}{2} . {(\frac{1}{2})}^{3} . 1^{2} = \frac{1}{16}$ .

Câu 3:

Trong các số dưới đây, số nào gần nhất với giá trị đơn thức $\frac{7}{5} x^{3} y^{2} z^{2}$ tại x = 2; y = -1; z = 1?

A. 11;

B. 12;

C. 10;

D. 13.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Thay x = 2; y = -1; z = 1 vào đơn thức $\frac{7}{5} x^{3} y^{2} z^{2}$ , ta có: $\frac{7}{5} . 2^{3} . {(‐ 1)}^{2} . 1^{2} = \frac{56}{5} = 11, 2$ .

Trong các số: 10, 11, 12, 13 thì 11 gần với 11,2 nhất nên đáp án đúng là A.

Câu 4:

Giá trị đơn thức $\frac{1}{2} x y^{3} . 3 x^{2} y$ tại $x = \frac{1}{2}; y = 2$ là

A. $\frac{3}{2}$ ;

B. $\frac{1}{2};$

C. 4;

D. 3

Xem đáp án

Câu 5:

Giá trị của đơn thức $\frac{1}{3} x y^{3} . (‐ 2) y$ tại x = -1; y = 3 là một số chia hết cho

A. 5;

B. 7;

C. 9;

D. 12.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Thu gọn đơn thức:

$\frac{1}{3} x y^{3} . (‐ 2) y = \frac{1}{3} . (‐ 2) . x (y^{3} . y) = \frac{‐ 2}{4} x y^{4}$ .

Thay x = -1; y = 3 vào đơn thức $\frac{‐ 2}{3} x y^{4}$ , ta có: $\frac{‐ 2}{3} . (‐ 1) . 3^{4} = 54$ , chia hết cho 9.

Câu 6:

Cho $\frac{1}{2} x y^{2} z = 1$ . Giá trị biểu thức $A = \frac{1}{3} x y^{2} z$ là

A. 1;

B. $\frac{2}{3}$ ;

C. $\frac{1}{3}$ ;

D. $\frac{1}{6}$ .

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có: $\frac{1}{2} x y^{2} z = 1$ suy ra xy²z = 2.

Thay xy²z = 2 vào $A = \frac{1}{3} x y^{2} z$ ta được: $A = \frac{1}{3} . 2 = \frac{2}{3}$ .

Câu 7:

Cho x³y² = 0,5. Giá trị của biểu thức B = -x²y.3xy - 2x³y² là:

A. 0,5;

B. -1,5;

C. 2,5;

D. -2,5.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

B = -x²y.3xy - 2x³y² = -3.(x².x).(y.y) - 2x³y² = -3x³y² - 2x³y² = -5x³y².

Thay x³y² = 0,5 vào B = -5x³y²ta có: B = -5.0,5 = -2,5.

Câu 8:

Cho 2xy = 1. Giá trị của biểu thức P = 4x²y² - 3x²y² là

A. $\frac{1}{2}$ ;

B. 1;

C. $\frac{5}{4}$ ;

D. $\frac{1}{4}$ .

Xem đáp án

Cho 2xy = 1. Giá trị của biểu thức P (ảnh 1)

Câu 9:

Cho biết: 3axy² + (-2axy²) = 12 với x = 3; y = 2. Giá trị của a là

A. –1;

B. 1;

C. 2;

D. –2.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có: 3axy² + (-2axy²) = (3 - 2)axy² = axy².

Với x = 3; y = 2 ta có: a.3.2² = 12a.

Theo bài, với x = 3; y = 2 ta có 3axy² + (-2axy²) = 12

Nên 12a = 12, do đó a = 1.

Câu 10:

Giá trị của đơn thức $\frac{‐ 1}{3} x^{3} y . {(2 x)}^{2}$ khi x = –1; y = |(–1) + x| là:

A. $\frac{‐ 4}{3}$ ;

B. $\frac{‐ 8}{3}$ ;

C. $\frac{8}{3}$ ;

D. $\frac{4}{3}$ .

Xem đáp án

Bắt đầu thi ngay

Trắc nghiệm Toán 8 Bài 1. Đơn thức

Dạng 4: Tìm giá trị đơn thức khi biết giá trị của biến

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương