Trắc nghiệm Toán 7 CTST Bài tập cuối chương 8 có đáp án (Phần 2) (Nhận biết)
-
281 lượt thi
-
8 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong tam giác vuông, góc đối diện với cạnh huyền là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì trong tam giác vuông góc đối diện với cạnh huyền là góc vuông và góc đối diện với các cạnh góc vuông là các góc nhọn.
Do đó B đúng
Vậy ta chọn phương án B.
Câu 2:
Cho ∆ABC có AB > BC > AC. Chọn khẳng định sai:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có “Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu độ dài của hai cạnh còn lại”.
Do đó AB > BC – AC, nên B đúng;
AC > AB – BC, nên C đúng.
Ta lại có “Trong một tam giác, độ dài một cạnh bao giờ cũng nhỏ hơn tổng độ dài của hai cạnh còn lại”.
Do đó AC < AB + BC, nên D đúng;
AB < BC – AC, nên A sai.
Vậy ta chọn phương án A.
Câu 3:
Cho hình vẽ
Biết ∆DEF = ∆MNP. Độ dài cạnh MP là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Theo bài ta có ∆DEF = ∆MNP
Suy ra DF = MN (hai cạnh tương ứng)
Mà DF = 11 cm (giả thiết)
Suy ra MP = 11 cm.
Vậy ta chọn phương án C.
Câu 4:
Tam giác cân có một góc bằng 60° là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Tam giác cân có một góc bằng 60° là tam giác đều.
Vậy ta chọn phương án B.
Câu 5:
Cho hình vẽ
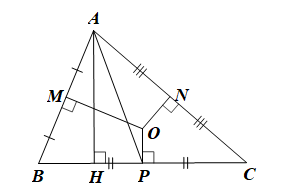
Tổng số đường trung trực có trong hình vẽ là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Quan sát hình vẽ ta có:
OP ⊥ BC tại trung điểm P của đoạn thẳng BC nên OP là đường trung trực của BC;
OM ⊥ AB tại trung điểm M của đoạn thẳng AB nên OM là trung trực của AB;
ON ⊥ AC tại trung điểm N của đoạn thẳng AC nên ON là trung trực của AC.
Do đó có tất cả 3 đường trung trực trong hình vẽ.
Vậy ta chọn phương án B.
Câu 6:
Cho tam giác ABC. Ba đường trung trực của tam giác ABC cùng đi qua một điểm M. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ba đường trung trực của tam giác ABC cùng đi qua một điểm M, điểm M này cách đều ba đỉnh của tam giác ABC.
Vậy ta chọn phương án A.
Câu 7:
Cho hình vẽ sau:
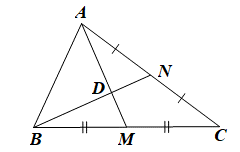
Biết AM = 3 cm, độ dài đoạn thẳng AD bằng
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại D nên D là trọng tâm tam giác ABC.
Suy ra AD = \(\frac{2}{3}\)AM (tính chất trọng tâm của tam giác).
Do đó AD = \(\frac{2}{3}\).3 = 2 (cm).
Vậy ta chọn phương án B.
Câu 8:
Cho tam giác MNP có các tia phân giác của góc M và N cắt nhau tại H. Khẳng định nào dưới đây là sai?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
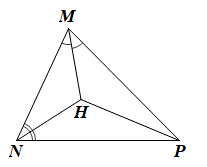
Ta có DMNP có MH và NH là hai tia phân giác của góc M và N cắt nhau tại H nên H là giao điểm ba đường phân giác của tam giác.
Do đó PH là tia phân giác của góc P.
Suy ra \(\widehat {MPH} = \widehat {NPH}\), \(\widehat {MPN} = 2\widehat {MPH}\) và \(\widehat {MPN} = 2\widehat {NPH}\).
Vậy ta chọn phương án C.