Trắc nghiệm Toán 7 Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác có đáp án
Dạng 3. Sử dụng tính chất trực tâm của tam giác để chứng minh hai đường thẳng vuông góc, ba đường thẳng đồng quy
-
484 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Khẳng định nào sau đây là đúng?
Xem đáp án
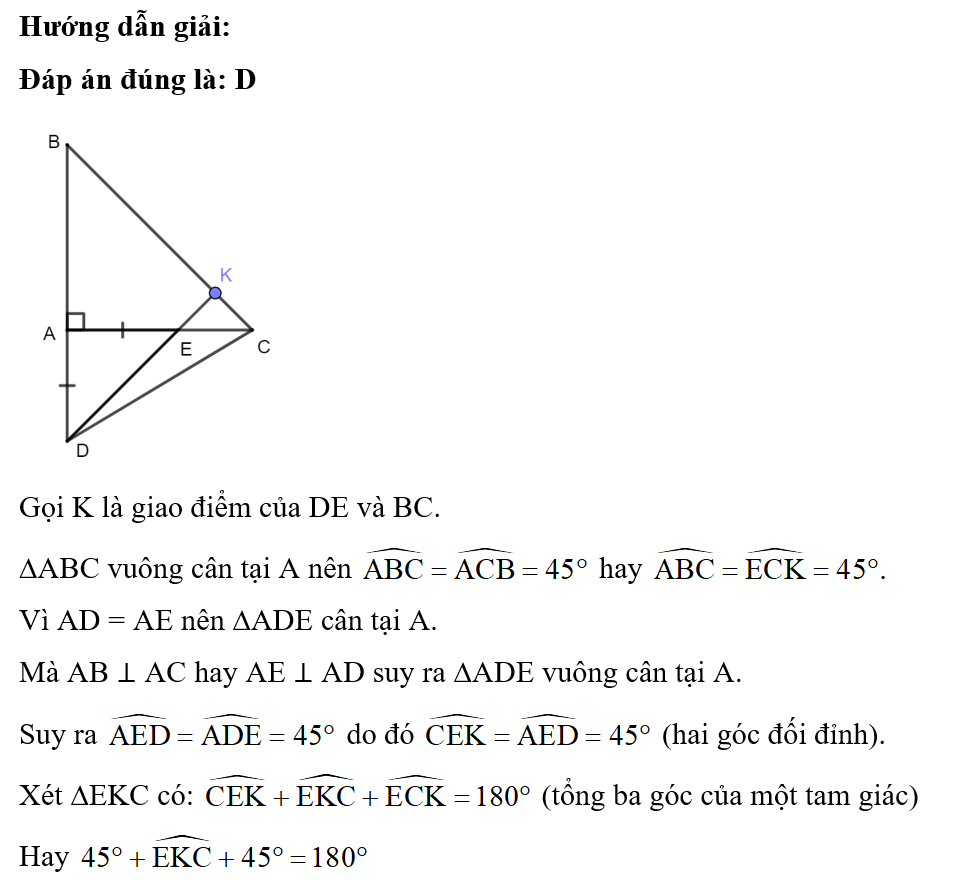
Hướng dẫn giải:
Đáp án đúng là: C
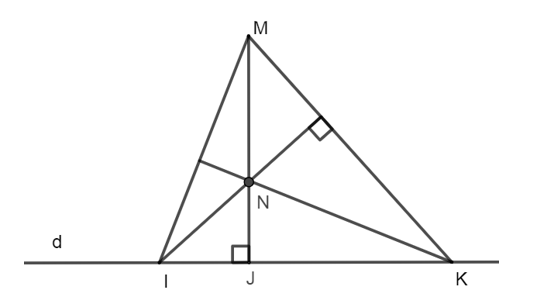
Ta có: MJ ⊥ IK tại J nên MJ là đường cao của ∆MIK.
Mà N nằm trên đường thẳng qua I và vuông góc với MK nên IN ⊥ MK.
Do đó IN là đường cao của ΔMIK.
Xét ∆MIK có hai đường cao IN và MJ cắt nhau tại N nên N là trực tâm của ΔMIK.
Suy ra KN là đường cao của ∆MIK hay KN ⊥ MI.
Câu 3:
Cho ∆MNP cân tại M, đường cao PQ cắt đường phân giác MS ở K. Khẳng định nào sau đây là sai?
Xem đáp án
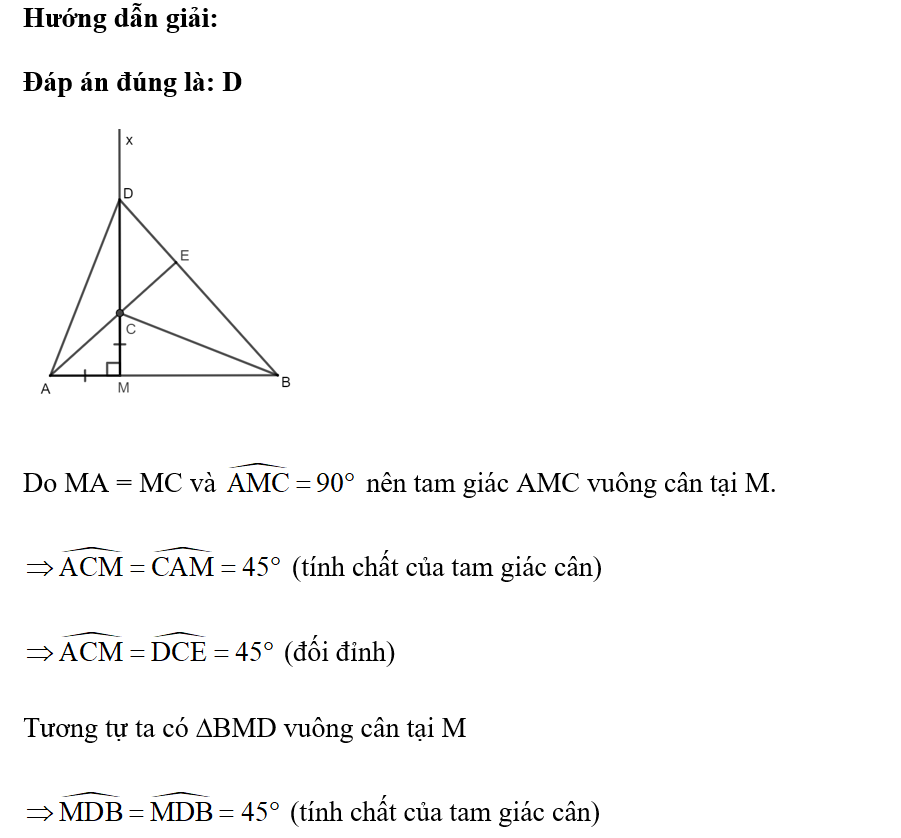
Hướng dẫn giải:
Đáp án đúng là: D
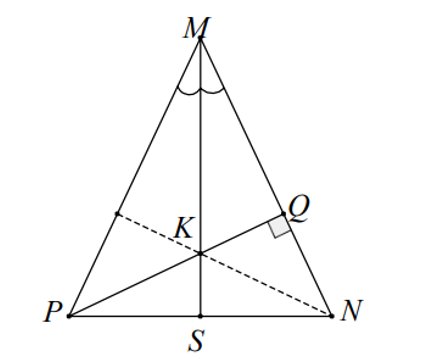
Xét ∆MPN cân tại M có MS là đường phân giác (giả thiết) nên MS đồng thời là đường cao. Suy ra MS ⊥ PN
∆MPN có MS ⊥ PN, PQ ⊥ MN và MS cắt PQ tại K nên K là trực tâm của ∆MPN.
Do đó NK ⊥ MP.
Vậy cả A, B, C đều là khẳng định đúng. Ta chọn phương án D.
Câu 4:
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Lấy điểm K thuộc đoạn thẳng HC. Qua K kẻ đường thẳng song song với AB, cắt AH tại D. Khẳng định nào sau đây là đúng nhất?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là:D
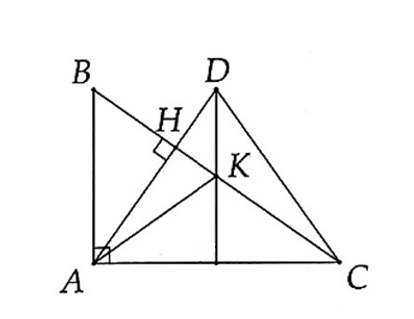
Vì AB ⊥ AC và DK // AB nên DK ⊥ AC.
Xét ∆ADC có: DK ⊥ AC, CH ⊥ AD và DK cắt CH tại K nên K là trực tâm ∆ADC.
Suy ra AK ⊥ CD và ba đường thẳng AK, DK, BC đồng quy.
Vậy cả A, B, C đều là khẳng định đúng. Ta chọn phương án D.
Câu 5:
Cho ∆ABC vuông tại A, đường cao AH, lấy I là trung điểm AC. Gọi K và D thứ tự là trung điểm của AH và HC. Khẳng định nào sau đây là sai?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
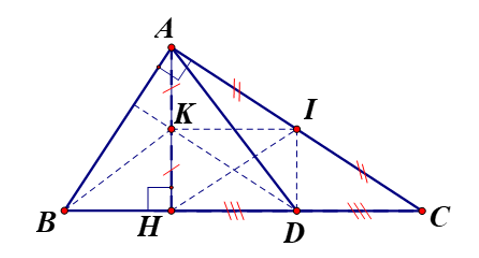
⦁ Trong ∆AHC vuông tại H, dễ dàng chứng minh được
Do đó I cách đều ba đỉnh của tam giác nên I là giao điểm ba trung trực của ∆AHC.
⦁ Ta có AH ⊥ BC, DI ⊥ BC suy ra AH // DI nên (so le trong);
AH ⊥ BC, IK ⊥ AK suy ra IK // BC nên (so le trong).
Xét ∆KHD và ∆DIK có:
KD là cạnh chung;
Do đó ∆KHD = ∆DIK (g.c.g).
Suy ra HK = ID, HD = IK (các cặp cạnh tương ứng)
Xét ∆KDH (vuông tại H) và ∆ICD (vuông tại D) có:
HK = ID (chứng minh trên);
HD = DC (do DI là trung trực của HC).
Do đó ∆KDH = ∆IDC (hai cạnh góc vuông).
Suy ra (hai góc tương ứng)
Mà hai góc này ở vị trí đồng vị nên DK // AC.
Lại có AB ⊥ AC nên DK ⊥ AB
Trong ∆ABD có: AH ⊥ BD (giả thiết), DK ⊥ AB và AH cắt DK tại K
Do đó K là trực tâm ∆ABD, suy ra BK ⊥ AD.
Câu 6:
Cho ∆ABC vuông tại A có đường cao AH. Gọi M là trung điểm của AH, qua M kẻ đường thẳng song song với AB. Gọi K là giao điểm của MN và AH.
Cho các khẳng định sau:
(I) CM là đường cao của ∆ANC;
(II) CM ⊥ AN;
(III) NK, AH và CM đồng quy tại M.
Có bao nhiêu khẳng định đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
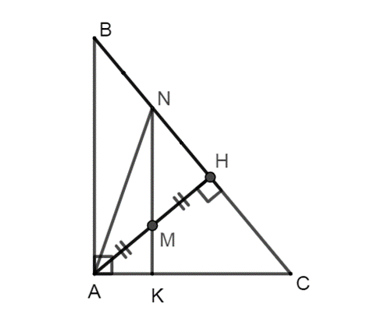
⦁ Trong ∆ABC có NK // AB mà AB ⊥ AC nên NK ⊥ AC.
Xét ∆ANC có: AH ⊥ NC, NK ⊥ AC và AH và NK giao nhau tại M.
Do đó M là trực tâm của ∆ANC suy ra CM là đường cao của ∆ANC nên CM ⊥ AN.
⦁ Ta có NK, AH và CM là ba đường cao của tam giác ANC nên đồng quy tại M.
Vậy khẳng định (I), (II) và (III) đều đúng. Ta chọn đáp án A.
Câu 7:
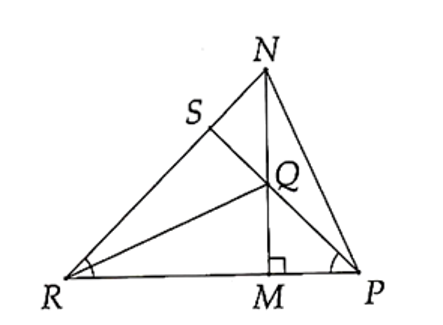
Cho tam giác LMN nhọn và điểm S nằm trong tam giác, LS cắt MN tại P, MS cắt LN tại Q. Nếu LP ⊥ MN, MQ ⊥ LN thì vị trí của NS và ML là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là:B
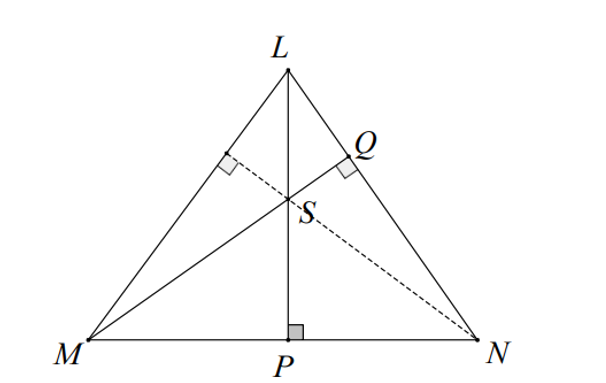
Nếu LP ⊥ MN, MQ ⊥ LN thì S là trực tâm của ∆LMN. Do đó MS ⊥ PN.
Câu 9:
∆ABC vuông tại A, kẻ đường cao AH. Lấy điểm K thuộc đoạn thẳng HC. Qua K kẻ đường thẳng song song với AB, cắt AH tại D. Khẳng định nào sau đây là sai?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
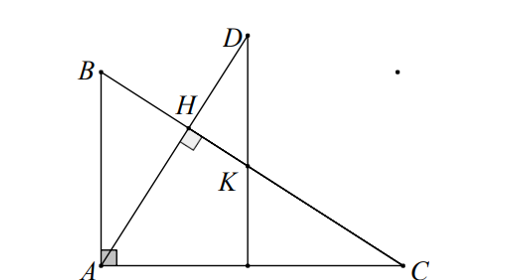
Ta có: AB ⊥ AC và DK // AB nên DK ⊥ AC (quan hệ từ vuông góc đến song song).
Lại có: CH ⊥ AD và DK giao CH tại K.
Do đó K là trực tâm của ∆ADC nên AK ⊥ CD.
Vậy phương án D là sai.
Câu 10:
Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP, trên tia đối của tia MP lấy điểm R sao cho MR = MN. Gọi S là giao điểm PQ và RN. Cho các khẳng định sau:
(I) PS ⊥ NR;
(II) MN, PS và RQ đồng quy tại Q.
Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
ΔMPQ vuông tại M có MQ = MP nên là tam giác vuông cân tại M, do đó
Suy ra (đối đỉnh)
Tương tự, ΔMNR vuông cân tại M có
Trong ΔNSQ có: và
Do đó nên QS ⊥ NS hay PS ⊥ NR.
Trong ΔNPR có các đường cao PS và MN cắt nhau tại Q.
Suy ra Q là trực tâm ΔNPR.
Ta có: MN, PS và RQ là ba đường cao của tam giác NPR nên đồng quy tại Q.