Câu hỏi:
26/01/2024 119
Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP, trên tia đối của tia MP lấy điểm R sao cho MR = MN. Gọi S là giao điểm PQ và RN. Cho các khẳng định sau:
(I) PS ⊥ NR;
(II) MN, PS và RQ đồng quy tại Q.
Khẳng định nào sau đây là đúng?
Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP, trên tia đối của tia MP lấy điểm R sao cho MR = MN. Gọi S là giao điểm PQ và RN. Cho các khẳng định sau:
(I) PS ⊥ NR;
(II) MN, PS và RQ đồng quy tại Q.
Khẳng định nào sau đây là đúng?
A. Chỉ (I) sai;
A. Chỉ (I) sai;
B. Chỉ (II) sai;
B. Chỉ (II) sai;
C. Cả (I), (II) đúng;
D. Cả (I), (II) sai.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C
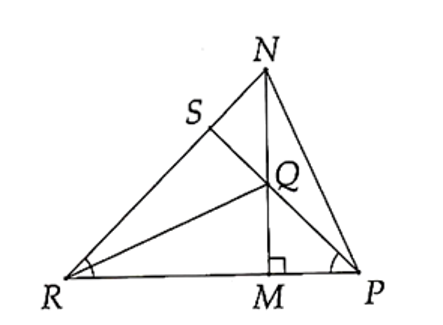
ΔMPQ vuông tại M có MQ = MP nên là tam giác vuông cân tại M, do đó
Suy ra (đối đỉnh)
Tương tự, ΔMNR vuông cân tại M có
Trong ΔNSQ có: và
Do đó nên QS ⊥ NS hay PS ⊥ NR.
Trong ΔNPR có các đường cao PS và MN cắt nhau tại Q.
Suy ra Q là trực tâm ΔNPR.
Ta có: MN, PS và RQ là ba đường cao của tam giác NPR nên đồng quy tại Q.
Hướng dẫn giải:
Đáp án đúng là: C

ΔMPQ vuông tại M có MQ = MP nên là tam giác vuông cân tại M, do đó
Suy ra (đối đỉnh)
Tương tự, ΔMNR vuông cân tại M có
Trong ΔNSQ có: và
Do đó nên QS ⊥ NS hay PS ⊥ NR.
Trong ΔNPR có các đường cao PS và MN cắt nhau tại Q.
Suy ra Q là trực tâm ΔNPR.
Ta có: MN, PS và RQ là ba đường cao của tam giác NPR nên đồng quy tại Q.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC vuông cân tại A, lấy E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Cho các khẳng định sau:
(I) ∆ADE vuông cân tại A.
(II) E là trực tâm của ∆BCD.
(III) BE ⊥ CD.
Có bao nhiêu khẳng định đúng?
Cho ∆ABC vuông cân tại A, lấy E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Cho các khẳng định sau:
(I) ∆ADE vuông cân tại A.
(II) E là trực tâm của ∆BCD.
(III) BE ⊥ CD.
Có bao nhiêu khẳng định đúng?
Câu 2:
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Lấy điểm K thuộc đoạn thẳng HC. Qua K kẻ đường thẳng song song với AB, cắt AH tại D. Khẳng định nào sau đây là đúng nhất?
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Lấy điểm K thuộc đoạn thẳng HC. Qua K kẻ đường thẳng song song với AB, cắt AH tại D. Khẳng định nào sau đây là đúng nhất?
Câu 3:
Cho đoạn thẳng AB và điểm M nằm giữa A và B (MA < MB). Vẽ tia Mx vuông góc với AB, trên đó lấy hai điểm C và D sao cho MA = MC, MD = MB. Tia AC cắt BD ở E. Khẳng định nào sau đây sai?
Cho đoạn thẳng AB và điểm M nằm giữa A và B (MA < MB). Vẽ tia Mx vuông góc với AB, trên đó lấy hai điểm C và D sao cho MA = MC, MD = MB. Tia AC cắt BD ở E. Khẳng định nào sau đây sai?
Câu 4:
Cho tam giác LMN nhọn và điểm S nằm trong tam giác, LS cắt MN tại P, MS cắt LN tại Q. Nếu LP ⊥ MN, MQ ⊥ LN thì vị trí của NS và ML là
Cho tam giác LMN nhọn và điểm S nằm trong tam giác, LS cắt MN tại P, MS cắt LN tại Q. Nếu LP ⊥ MN, MQ ⊥ LN thì vị trí của NS và ML là
Câu 5:
Cho ∆ABC vuông tại A, đường cao AH, lấy I là trung điểm AC. Gọi K và D thứ tự là trung điểm của AH và HC. Khẳng định nào sau đây là sai?
Cho ∆ABC vuông tại A, đường cao AH, lấy I là trung điểm AC. Gọi K và D thứ tự là trung điểm của AH và HC. Khẳng định nào sau đây là sai?
Câu 6:
∆ABC vuông tại A, kẻ đường cao AH. Lấy điểm K thuộc đoạn thẳng HC. Qua K kẻ đường thẳng song song với AB, cắt AH tại D. Khẳng định nào sau đây là sai?
∆ABC vuông tại A, kẻ đường cao AH. Lấy điểm K thuộc đoạn thẳng HC. Qua K kẻ đường thẳng song song với AB, cắt AH tại D. Khẳng định nào sau đây là sai?
Câu 7:
Cho ∆ABC vuông tại A có đường cao AH. Gọi M là trung điểm của AH, qua M kẻ đường thẳng song song với AB. Gọi K là giao điểm của MN và AH.
Cho các khẳng định sau:
(I) CM là đường cao của ∆ANC;
(II) CM ⊥ AN;
(III) NK, AH và CM đồng quy tại M.
Có bao nhiêu khẳng định đúng?
Cho ∆ABC vuông tại A có đường cao AH. Gọi M là trung điểm của AH, qua M kẻ đường thẳng song song với AB. Gọi K là giao điểm của MN và AH.
Cho các khẳng định sau:
(I) CM là đường cao của ∆ANC;
(II) CM ⊥ AN;
(III) NK, AH và CM đồng quy tại M.
Có bao nhiêu khẳng định đúng?
Câu 8:
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Khẳng định nào sau đây là đúng?
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Khẳng định nào sau đây là đúng?
Câu 9:
Cho ∆MNP cân tại M, đường cao PQ cắt đường phân giác MS ở K. Khẳng định nào sau đây là sai?
Cho ∆MNP cân tại M, đường cao PQ cắt đường phân giác MS ở K. Khẳng định nào sau đây là sai?


