Trắc nghiệm Toán 7 Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác có đáp án
Dạng 1. Nhận biết đường trung trực, đường cao trong tam giác
-
580 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong một tam giác, tâm của đường tròn đi qua ba đỉnh của tam giác là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Trong một tam giác, giao điểm của ba đường trung trực cách đều ba đỉnh.
Do đó tâm của đường tròn đi qua ba đỉnh của tam giác là giao điểm của ba đường trung trực.
Câu 2:
Cho tam giác ABC cân tại A có các đường trung tuyến AM, BN, CP. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
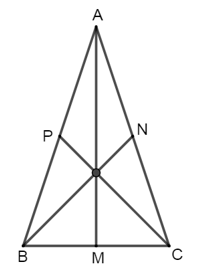
Xét ∆AMB và ∆AMC có:
AB = AC (do ∆ABC cân tại A);
AM là cạnh chung;
MB = MC (vì AM là trung tuyến)
Suy ra ∆AMB = ∆AMC (c.c.c).
Do đó: (hai góc tương ứng).
Mà (kề bù).
Suy ra nên AM ⊥ BC tại M
Mà M là trung điểm của BC.
Do đó AM là đường trung trực của BC.
Hay AM là đường trung trực của tam giác ABC. Do đó khẳng định A đúng.
Câu 3:
Cho tam giác ABC vuông tại A. Trực tâm của tam giác ABC
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
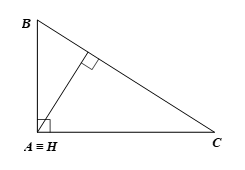
Trực tâm của tam giác ABC vuông tại A là điểm A.
Câu 4:
Cho các hình vẽ sau:
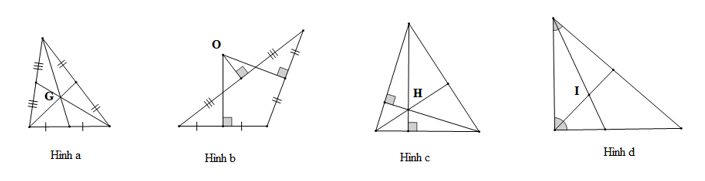
Trong các hình, hình nào có giao điểm của ba đường trung trực trong một tam giác?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì đường trung trực của tam giác là đường vuông góc với mỗi cạnh tại trung điểm của cạnh đó nên điểm O trong hình b là giao điểm của ba đường trung trực trong tam giác đó.
Vậy ta chọn phương án B.
Câu 5:
Cho tam giác ABC có M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại O. Số đo góc OMC là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
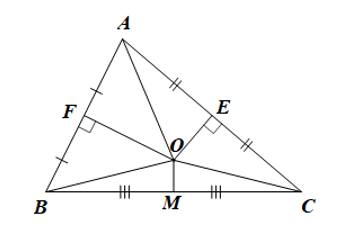
Do các đường trung trực của AB và AC cắt nhau tại O nên O là giao điểm của ba đường trung trực của tam giác ABC.
Do đó O nằm trên đường trung trực của BC.
Mà M là trung điểm của BC nên OM là trung trực của BC.
Suy ra OM vuông góc với BC nên .
Vậy ta chọn phương án A.
Câu 6:
Cho ∆GFK có FK < GF, phân giác FH. Trên GF lấy điểm J sao cho FK = FJ. Cho các khẳng định sau:
(I) HF là đường trung trực của JK;
(II) JK là đường trung tuyến của ∆GFK;
(III) HF là đường cao của ∆FJK.
Có bao nhiêu khẳng định đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
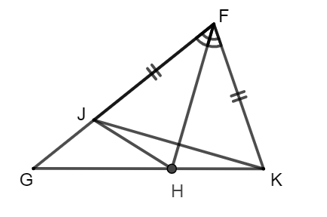
Xét ∆FHK và ∆FHJ có:
FH là cạnh chung;
(Vì FH là tia phân giác của ∆GFK);
JF = KF (giả thiết)
Do đó ∆FHK = ∆FHJ (c.g.c).
Suy ra JH = KH (hai cạnh tương ứng) nên H nằm trên đường trung trực của JK.
Mà JF = FK nên F cũng nằm trên đường trung trực của JK.
Do đó HF là đường trung trực của JK.
Từ đó HF ⊥ JK nên FH cũng là đường cao của tam giác FJK.
Do đó có hai khẳng định đúng là (I) và (III).
Vậy ta chọn phương án C.
Câu 7:
Cho ∆ABC cân tại A có AM ⊥ BC tại M. Phát biểu nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
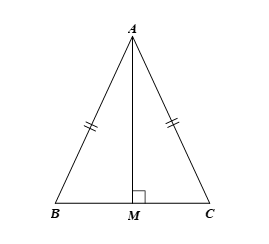
Vì ∆ABC cân tại A có AM ⊥ BC nên AM là đường cao.
Suy ra AM cũng là đường trung tuyến, đường trung trực và đường phân giác của ∆ABC.
Vậy ta chọn phương án D.
Câu 8:
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Khẳng định nào sau đây đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
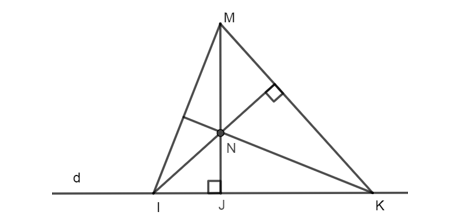
Ta có: MJ ⊥ IK tại J nên MJ là đường cao của ∆MIK.
Mà N nằm trên đường thẳng qua I và vuông góc với MK nên IN ⟘ MK.
Do đó IN là đường cao của ΔMIK.
Xét ∆MIK có hai đường cao IN và MJ cắt nhau tại N nên N là trực tâm của ΔMIK.
Do đó KN là đường cao của ∆MIK.
Vậy cả A, B, C đều là khẳng định đúng. Vậy ta chọn phương án D.
Câu 10:
Cho đoạn thẳng AB và điểm M nằm giữa A và B (MA < MB). Vẽ tia Mx vuông góc với AB tại M, trên tia Mx lấy hai điểm C và D sao cho MA = MC, MD = MB. Tia AC vuông cắt BD tại E. Khẳng định nào sau đây là sai?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
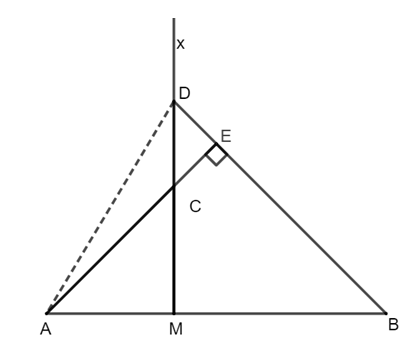
Do MA = MC và nên tam giác AMC vuông cân tại M
Do đó nên (đối đỉnh với góc ACM).
Tương tự, ta có ∆BMD vuông cân tại M nên
Từ đó suy ra
Suy ra hay AC ⊥ BD.
Trong ∆ABD, hai đường cao AE và DM cắt nhau nên C là trực tâm của ∆ABD.
Do đó BC là đường cao thứ ba của ∆ABD.
Khi đó A, B, C đều là khẳng định đúng.
Vậy phương án D là khẳng định sai. Ta chọn phương án D.