Trắc nghiệm Toán 6 KNTT Bài 9. Các dạng toán về phép cộng và phép trừ phân số có đáp án
-
136 lượt thi
-
22 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Phép cộng phân số có tính chất nào dưới đây?
 Xem đáp án
Xem đáp án
Trả lời:
Phép cộng phân số có các tính chất:
+) Tính chất giao hoán: khi đổi chỗ các phân số trong một tổng thì tổng không đổi.
+) Tính chất kết hợp: Muốn cộng một tổng hai phân số với phân số thứ ba, ta có thể cộng phân số thứ nhất với tổng hai phân số còn lại.
+) Tính chất cộng với 0: tổng của một phân số với 0 bằng chính phân số đó.
Đáp án cần chọn là: D
Câu 2:
 Xem đáp án
Xem đáp án
Trả lời:
\[\frac{{65}}{{91}} + \frac{{ - 44}}{{55}} = \frac{5}{7} + \frac{{ - 4}}{5} = \frac{{25}}{{35}} + \frac{{ - 28}}{{35}} = \frac{{ - 3}}{{35}}\]
Đáp án cần chọn là: C
Câu 3:
Chọn câu sai
 Xem đáp án
Xem đáp án
Trả lời:
Đáp án A: \[\frac{3}{2} + \frac{2}{3} = \frac{9}{6} + \frac{4}{6} = \frac{{13}}{6} > 1\] nên A đúng
Đáp án B: \[\frac{3}{2} + \frac{2}{3} = \frac{9}{6} + \frac{4}{6} = \frac{{13}}{6}\] nên B đúng
Đáp án C: \[\frac{3}{4} + \left( {\frac{{ - 4}}{{17}}} \right) = \frac{{51}}{{68}} + \frac{{ - 16}}{{68}} = \frac{{35}}{{68}}\] nên C đúng
Đáp án D: \[\frac{4}{{12}} + \frac{{21}}{{36}} = \frac{4}{{12}} + \frac{7}{{12}} = \frac{{11}}{{12}} < 1\] nên D sai
Đáp án cần chọn là: D
Câu 4:
Tìm x biết \[x - \frac{1}{5} = 2 + \frac{{ - 3}}{4}\]
 Xem đáp án
Xem đáp án
Trả lời:
\[x - \frac{1}{5} = 2 + \frac{{ - 3}}{4}\]
\[x - \frac{1}{5} = \frac{5}{4}\]
\[x = \frac{5}{4} + \frac{1}{5}\]
\[x = \frac{{29}}{{20}}\]
Đáp án cần chọn là: B
Câu 5:
Tính hợp lí biểu thức \[\frac{{ - 9}}{7} + \frac{{13}}{4} + \frac{{ - 1}}{5} + \frac{{ - 5}}{7} + \frac{3}{4}\] ta được kết quả là
 Xem đáp án
Xem đáp án
Trả lời:
\[\frac{{ - 9}}{7} + \frac{{13}}{4} + \frac{{ - 1}}{5} + \frac{{ - 5}}{7} + \frac{3}{4}\]
\[ = \left( {\frac{{ - 9}}{7} + \frac{{ - 5}}{7}} \right) + \left( {\frac{{13}}{4} + \frac{3}{4}} \right) + \frac{{ - 1}}{5}\]
\[ = \frac{{ - 14}}{7} + \frac{{16}}{4} + \frac{{ - 1}}{5}\]
\[ = \left( { - 2} \right) + 4 + \frac{{ - 1}}{5}\]
\[ = 2 + \frac{{ - 1}}{5}\]
\[ = \frac{{10}}{5} + \frac{{ - 1}}{5}\]
\[ = \frac{9}{5}\]
Đáp án cần chọn là: A
Câu 6:
 Xem đáp án
Xem đáp án
Trả lời:
\[M = \left( {\frac{{21}}{{31}} + \frac{{ - 16}}{7}} \right) + \left( {\frac{{44}}{{53}} + \frac{{10}}{{31}}} \right) + \frac{9}{{53}}\]
\[M = \frac{{21}}{{31}} + \frac{{ - 16}}{7} + \frac{{44}}{{53}} + \frac{{10}}{{31}} + \frac{9}{{53}}\]
\[M = \left( {\frac{{21}}{{31}} + \frac{{10}}{{31}}} \right) + \left( {\frac{{44}}{{53}} + + \frac{9}{{53}}} \right) + \frac{{ - 16}}{7}\]
\[M = 1 + 1 + \frac{{ - 16}}{7}\]
\[M = 2 + \frac{{ - 16}}{7}\]
\[M = \frac{{ - 2}}{7}\]
\[N = \frac{1}{2} + \frac{{ - 1}}{5} + \frac{{ - 5}}{7} + \frac{1}{6} + \frac{{ - 3}}{{35}} + \frac{1}{3} + \frac{1}{{41}}\]
\[N = \left( {\frac{1}{2} + \frac{1}{6} + \frac{1}{3}} \right) + \left( {\frac{{ - 1}}{5} + \frac{{ - 5}}{7} + \frac{{ - 3}}{{35}}} \right) + \frac{1}{{41}}\]
\[N = \frac{{3 + 1 + 2}}{6} + \frac{{\left( { - 7} \right) + \left( { - 25} \right) + \left( { - 3} \right)}}{{35}} + \frac{1}{{41}}\]
\[N = 1 + \left( { - 1} \right) + \frac{1}{{41}}\]
\[N = \frac{1}{{41}}\]
Đáp án cần chọn là: D
Câu 7:
Tìm tập hợp các số nguyên n để \[\frac{{n - 8}}{{n + 1}} + \frac{{n + 3}}{{n + 1}}\] là một số nguyên
 Xem đáp án
Xem đáp án
Trả lời:
Ta có:
\[\frac{{n - 8}}{{n + 1}} + \frac{{n + 3}}{{n + 1}} = \frac{{n - 8 + n + 3}}{{n + 1}}\]
\[\frac{{2n - 5}}{{n + 1}} = \frac{{\left( {2n + 2} \right) - 7}}{{n + 1}} = \frac{{2\left( {n + 1} \right) - 7}}{{n + 1}}\]
\[\frac{{2\left( {n + 1} \right)}}{{n + 1}} - \frac{7}{{n + 1}} = 2 - \frac{7}{{n + 1}}\]
Yêu cầu bài toán thỏa mãn nếu \[\frac{7}{{n + 1}} \in Z\] hay \[n + 1 \in U\left( 7 \right) = \left\{ { \pm 1; \pm 7} \right\}\]
Ta có bảng:
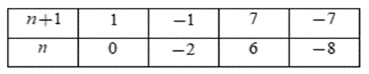
Vậy n ∈ {0; −2; 6; −8}
Đáp án cần chọn là: C
Câu 8:
Có bao nhiêu số nguyên x thỏa mãn \[\frac{{15}}{{41}} + \frac{{ - 138}}{{41}} \le x < \frac{1}{2} + \frac{1}{3} + \frac{1}{6}\]?
 Xem đáp án
Xem đáp án
Trả lời:
\[\frac{{15}}{{41}} + \frac{{ - 138}}{{41}} \le x < \frac{1}{2} + \frac{1}{3} + \frac{1}{6}\]
\[ - 3 \le x < 1\]
\[x \in \left\{ { - 3; - 2; - 1;0} \right\}\]
Đáp án cần chọn là: D
Câu 9:
Tính tổng \[A = \frac{1}{2} + \frac{1}{6} + \frac{1}{{12}} + ... + \frac{1}{{99.100}}\] ta được
 Xem đáp án
Xem đáp án
Trả lời:
\[A = \frac{1}{2} + \frac{1}{6} + \frac{1}{{12}} + ... + \frac{1}{{99.100}}\]
\[A = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{99.100}}\]
\[A = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{{99}} - \frac{1}{{100}}\]
\[A = 1 - \frac{1}{{100}} = \frac{{99}}{{100}}\]
So sánh A với \[\frac{3}{5}\] và \[\frac{4}{5}\]
Ta có: \[\frac{3}{5} = \frac{{60}}{{100}};\frac{4}{5} = \frac{{80}}{{100}}\]
\[ \Rightarrow \frac{{60}}{{100}} < \frac{{80}}{{100}} < \frac{{99}}{{100}} \Rightarrow A > \frac{4}{5} > \frac{3}{5}\]
Đáp án cần chọn là: D
Câu 10:
Cho \[S = \frac{1}{{21}} + \frac{1}{{22}} + \frac{1}{{23}} + ... + \frac{1}{{35}}\]
Chọn câu đúng
 Xem đáp án
Xem đáp án
Trả lời:
\[S = \frac{1}{{21}} + \frac{1}{{22}} + \frac{1}{{23}} + ... + \frac{1}{{35}}\]
\[S = \left( {\frac{1}{{21}} + ... + \frac{1}{{25}}} \right) + \left( {\frac{1}{{26}} + ... + \frac{1}{{30}}} \right) + \left( {\frac{1}{{31}}... + \frac{1}{{35}}} \right)\]
\[S > \left( {\frac{1}{{25}} + ... + \frac{1}{{25}}} \right) + \left( {\frac{1}{{30}} + ... + \frac{1}{{30}}} \right) + \left( {\frac{1}{{35}}... + \frac{1}{{35}}} \right)\]
\[S > \frac{1}{5} + \frac{1}{6} + \frac{1}{7} = \frac{{107}}{{210}} > \frac{1}{2}\]
Vậy \[S > \frac{1}{2}\]
Đáp án cần chọn là: A
Câu 11:
Có bao nhiêu cặp số \[a;b \in Z\] thỏa mãn \[\frac{a}{5} + \frac{1}{{10}} = \frac{{ - 1}}{b}\]?
 Xem đáp án
Xem đáp án
Trả lời:
\[\frac{a}{5} + \frac{1}{{10}} = \frac{{ - 1}}{b}\]
\[\frac{{2a}}{{10}} + \frac{1}{{10}} = \frac{{ - 1}}{b}\]
\[\frac{{2a + 1}}{{10}} = \frac{{ - 1}}{b}\]
\[\left( {2a + 1} \right).b = - 10\]
2a + 1 là số lẻ; 2a + 1 là ước của −10
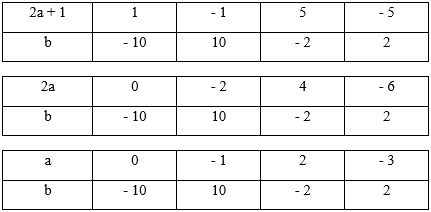
Vậy có 4 cặp số (a; b) thỏa mãn bài toán.
Đáp án cần chọn là: C
Câu 12:
Cặp phân số nào sau đây là hai số đối nhau?
 Xem đáp án
Xem đáp án
Trả lời:
Đáp án A: Số đối của \[\frac{{ - 2}}{3}\]là \[\frac{2}{3}\] chứ không phải \[\frac{3}{2}\] nên A sai.
Đáp án B: Số đối của \[\frac{{ - 12}}{{13}}\]là \[\frac{{12}}{{13}}\] chứ không phải \[;\frac{{13}}{{ - 12}}\] nên B sai.
Đáp án C: Số đối của \[\frac{1}{2}\] là \[ - \frac{1}{2}\]nên C đúng.
Đáp án D: Số đối của \[\frac{3}{4}\] là \[\frac{{ - 3}}{4}\]hoặc \[\frac{3}{{ - 4}}\]hoặc \[ - \frac{3}{4}\]chứ không phải \[\frac{{ - 4}}{3}\]nên D sai.
Đáp án cần chọn là: C
Câu 13:
Số đối của \[ - \left( { - \frac{2}{{27}}} \right)\] là:
 Xem đáp án
Xem đáp án
Trả lời:
Ta có: \[ - \left( { - \frac{2}{{27}}} \right) = \frac{2}{{27}}\] nên số đối của \[\frac{2}{{27}}\] là \[ - \frac{2}{{27}}\]
Đáp án cần chọn là: D
Câu 14:
Tính \[\frac{{ - 1}}{6} - \frac{{ - 4}}{9}\]
 Xem đáp án
Xem đáp án
Trả lời:
\[\frac{{ - 1}}{6} - \frac{{ - 4}}{9} = \frac{{ - 1}}{6} + \frac{4}{9} = \frac{{ - 3}}{{18}} + \frac{8}{{18}} = \frac{5}{{18}}\]
Đáp án cần chọn là: A
Câu 15:
Chọn câu đúng
 Xem đáp án
Xem đáp án
Trả lời:
Đáp án A: \[\frac{4}{{13}} - \frac{1}{2} = \frac{8}{{26}} - \frac{{13}}{{26}} = \frac{{ - 5}}{{26}} \ne \frac{5}{{26}}\]nên A sai.
Đáp án B: \[\frac{1}{2} - \frac{1}{3} = \frac{3}{6} - \frac{2}{6} = \frac{1}{6} \ne \frac{5}{6}\] nên B sai.
Đáp án C: \[\frac{{17}}{{20}} - \frac{1}{5} = \frac{{17}}{{20}} - \frac{4}{{20}} = \frac{{13}}{{20}}\] nên C đúng.
Đáp án D: \[\frac{5}{{15}} - \frac{1}{3} = \frac{1}{3} - \frac{1}{3} = 0 \ne \frac{1}{5}\] nên D sai.
Đáp án cần chọn là: C
Câu 16:
Tính hợp lí \[B = \frac{{31}}{{23}} - \left( {\frac{7}{{30}} + \frac{8}{{23}}} \right)\] ta được
 Xem đáp án
Xem đáp án
Trả lời:
\[B = \frac{{31}}{{23}} - \left( {\frac{7}{{30}} + \frac{8}{{23}}} \right)\]
\[B = \frac{{31}}{{23}} - \frac{7}{{30}} - \frac{8}{{23}}\]
\[B = \left( {\frac{{31}}{{23}} - \frac{8}{{23}}} \right) - \frac{7}{{30}}\]
\[B = 1 - \frac{7}{{30}}\]
\[B = \frac{{23}}{{30}}\]
Đáp án cần chọn là: A
Câu 17:
Cho \[M = \left( {\frac{1}{3} + \frac{{12}}{{67}} + \frac{{13}}{{41}}} \right) - \left( {\frac{{79}}{{67}} - \frac{{28}}{{41}}} \right)\] và \[N = \frac{{38}}{{45}} - \left( {\frac{8}{{45}} - \frac{{17}}{{51}} - \frac{3}{{11}}} \right)\]. Chọn câu đúng
 Xem đáp án
Xem đáp án
Trả lời:
\[M = \left( {\frac{1}{3} + \frac{{12}}{{67}} + \frac{{13}}{{41}}} \right) - \left( {\frac{{79}}{{67}} - \frac{{28}}{{41}}} \right)\]
\[M = \frac{1}{3} + \frac{{12}}{{67}} + \frac{{13}}{{41}} - \frac{{79}}{{67}} + \frac{{28}}{{41}}\]
\[M = \frac{1}{3} + \left( {\frac{{12}}{{67}} - \frac{{79}}{{67}}} \right) + \left( {\frac{{13}}{{41}} + \frac{{28}}{{41}}} \right)\]
\[M = \frac{1}{3} + \left( { - 1} \right) + 1\]
\[M = \frac{1}{3}\]
\[N = \frac{{38}}{{45}} - \left( {\frac{8}{{45}} - \frac{{17}}{{51}} - \frac{3}{{11}}} \right)\]
\[N = \frac{{38}}{{45}} - \frac{8}{{45}} + \frac{{17}}{{51}} + \frac{3}{{11}}\]
\[N = \left( {\frac{{38}}{{45}} - \frac{8}{{45}}} \right) + \frac{{17}}{{51}} + \frac{3}{{11}}\]
\[N = \frac{2}{3} + \frac{1}{3} + \frac{3}{{11}}\]
\[N = 1 + \frac{3}{{11}}\]
\[N = \frac{{14}}{{11}}\]
Vì \[\frac{1}{3} < 1 < \frac{{14}}{{11}}\] nên M < 1 < N
Đáp án cần chọn là: D
Câu 18:
Tìm x sao cho \[x - \frac{{ - 7}}{{12}} = \frac{{17}}{{18}} - \frac{1}{9}\]
 Xem đáp án
Xem đáp án
Trả lời:
\[x - \frac{{ - 7}}{{12}} = \frac{{17}}{{18}} - \frac{1}{9}\]
\[x - \frac{{ - 7}}{{12}} = \frac{5}{6}\]
\[x = \frac{5}{6} + \frac{{ - 7}}{{12}}\]
\[x = \frac{1}{4}\]
Đáp án cần chọn là: C
Câu 19:
Giá trị nào của x dưới đây thỏa mãn \[\frac{{29}}{{30}} - \left( {\frac{{13}}{{23}} + x} \right) = \frac{7}{{69}}\]
 Xem đáp án
Xem đáp án
Trả lời:
\[\frac{{29}}{{30}} - \left( {\frac{{13}}{{23}} + x} \right) = \frac{7}{{69}}\]
\[\frac{{13}}{{23}} + x = \frac{{29}}{{30}} - \frac{7}{{69}}\]
\[x = \frac{{199}}{{230}} - \frac{{13}}{{23}}\]
\[x = \frac{3}{{10}}\]
Đáp án cần chọn là: A
Câu 20:
Có bao nhiêu số nguyên x thỏa mãn \[\frac{{ - 5}}{{14}} - \frac{{37}}{{14}} \le x \le \frac{{31}}{{73}} - \frac{{31313131}}{{73737373}}\]?
 Xem đáp án
Xem đáp án
Trả lời:
\[\frac{{ - 5}}{{14}} - \frac{{37}}{{14}} \le x \le \frac{{31}}{{73}} - \frac{{31313131}}{{73737373}}\]
\[\frac{{ - 5}}{{14}} + \frac{{ - 37}}{{14}} \le x \le \frac{{31}}{{73}} - \frac{{31313131:10101}}{{73737373:10101}}\]
\[\frac{{ - 42}}{{14}} \le x \le \frac{{31}}{{73}} - \frac{{31}}{{73}}\]
\[ - 3 \le x \le 0\]
\[x \in \left\{ { - 3; - 2; - 1;0} \right\}\]
Vậy có 4 giá trị của x thỏa mãn bài toán.
Đáp án cần chọn là: CCâu 21:
Cho x là số thỏa mãn \[x + \frac{4}{{5.9}} + \frac{4}{{9.13}} + \frac{4}{{13.17}} + ... + \frac{4}{{41.45}} = \frac{{ - 37}}{{45}}\]. Chọn kết luận đúng:
 Xem đáp án
Xem đáp án
Trả lời:
\[x + \frac{4}{{5.9}} + \frac{4}{{9.13}} + \frac{4}{{13.17}} + ... + \frac{4}{{41.45}} = \frac{{ - 37}}{{45}}\]
\[x + \frac{1}{5} - \frac{1}{9} + \frac{1}{9} - \frac{1}{{13}} + ... + \frac{1}{{41}} - \frac{1}{{45}} = \frac{{ - 37}}{{45}}\]
\[x + \frac{1}{5} - \frac{1}{{45}} = \frac{{ - 37}}{{45}}\]
\[x + \frac{8}{{45}} = \frac{{ - 37}}{{45}}\]
\[x = - \frac{{37}}{{45}} - \frac{8}{{45}}\]
\[x = - 1\]
Vì −1 là số nguyên âm nên đáp án A đúng.
Đáp án cần chọn là: A
Câu 22:
 Xem đáp án
Xem đáp án
Trả lời:
\[P = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{2002}^2}}} + \frac{1}{{{{2003}^2}}}\]
\[ < \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{2001.2002}} + \frac{1}{{2002.2003}}\]
\[ = \frac{1}{1} - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + ... + \frac{1}{{2001}} - \frac{1}{{2002}} + \frac{1}{{2002}} - \frac{1}{{2003}}\]
\[ = 1 - \frac{1}{{2003}} = \frac{{2002}}{{2003}} < 1\]
Vậy P < 1
Đáp án cần chọn là: C
