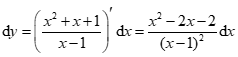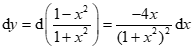Trắc nghiệm Toán 11 Bài 4: Trắc nghiệm vi phân của hàm số có đáp án (Mới nhất)
Trắc nghiệm Toán 11 Bài 4: Trắc nghiệm vi phân của hàm số có đáp án (Mới nhất)
-
72 lượt thi
-
34 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số \(y = f\left( x \right) = {\left( {x - 1} \right)^2}\). Biểu thức nào sau đây chỉ vi phân của hàm số\(f\left( x \right)\)?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn A.
Ta có \({\rm{d}}y = f'\left( x \right){\rm{d}}x = 2\left( {x - 1} \right){\rm{d}}x\).
Câu 2:
Tìm vi phân của các hàm số \(y = {x^3} + 2{x^2}\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
\(dy = (3{x^2} + 4x)dx\)
Câu 3:
Tìm vi phân của các hàm số \(y = \sqrt {3x + 2} \)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
\(dy = \frac{3}{{2\sqrt {3x + 2} }}dx\)
Câu 4:
Cho hàm số \(y = {x^3} - 9{x^2} + 12x - 5\). Vi phân của hàm số là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn A.
Ta có \({\rm{d}}y = {\left( {{x^3} - 9{x^2} + 12x - 5} \right)^\prime }{\rm{d}}x = \left( {3{x^2} - 18x + 12} \right){\rm{d}}x\).
Câu 5:
Tìm vi phân của các hàm số \(y = {(3x + 1)^{10}}\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
\(dy = 30{(3x + 1)^9}dx\).
Câu 6:
Tìm vi phân của các hàm số \(y = \sin 2x + {\sin ^3}x\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn B.
\(dy = \left( {2\cos 2x + 3{{\sin }^2}x\cos x} \right)dx\)
Câu 7:
Tìm vi phân của các hàm số \(y = \tan 2x\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
\(dy = 2(1 + {\tan ^2}2x)dx\)
Câu 8:
Tìm vi phân của các hàm số \(y = \sqrt[3]{{x + 1}}\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
\(dy = \frac{1}{{3\sqrt[3]{{{{(x + 1)}^2}}}}}dx\)
Câu 9:
Xét hàm số \(y = f\left( x \right) = \sqrt {1 + {{\cos }^2}2x} \). Chọn câu đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn B.
Ta có : \({\rm{d}}y = f'\left( x \right){\rm{d}}x\) \( = \frac{{{{\left( {1 + {{\cos }^2}2x} \right)}^\prime }}}{{2\sqrt {1 + {{\cos }^2}2x} }}{\rm{d}}x\)\( = \frac{{ - 4\cos 2x.\sin 2x}}{{2\sqrt {1 + {{\cos }^2}2x} }}{\rm{d}}x\)\( = \frac{{ - \sin 4x}}{{\sqrt {1 + {{\cos }^2}2x} }}{\rm{d}}x\).
Câu 10:
Cho hàm số\(y = {x^3} - 5x + 6\) . Vi phân của hàm số là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn A.
Ta có \({\rm{d}}y = {\left( {{x^3} - 5x + 6} \right)^\prime }{\rm{d}}x = \left( {3{x^2} - 5} \right){\rm{d}}x\).
Câu 11:
Cho hàm số \(y = \frac{1}{{3{x^3}}}\). Vi phân của hàm số là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn C.
Ta có \({\rm{d}}y = {\left( {\frac{1}{{3{x^3}}}} \right)^\prime }{\rm{d}}x = \frac{1}{3}.\frac{{3{x^2}}}{{{{\left( {{x^3}} \right)}^2}}} = - \frac{1}{{{x^4}}}{\rm{d}}x\).
Câu 12:
Cho hàm số \(y = \frac{{x + 2}}{{x - 1}}\). Vi phân của hàm số là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn C.
Ta có \({\rm{d}}y = {\left( {\frac{{x + 2}}{{x - 1}}} \right)^\prime }{\rm{d}}x = - \frac{3}{{{{\left( {x - 1} \right)}^2}}}{\rm{d}}x\).
Câu 13:
Cho hàm số \(y = \frac{{{x^2} + x + 1}}{{x - 1}}\). Vi phân của hàm số là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
Ta có \({\rm{d}}y = {\left( {\frac{{{x^2} + x + 1}}{{x - 1}}} \right)^\prime }{\rm{d}}x\)\( = \frac{{\left( {2x + 1} \right)\left( {x - 1} \right) - \left( {{x^2} + x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}{\rm{d}}x\)\( = \frac{{{x^2} - 2x - 2}}{{{{\left( {x - 1} \right)}^2}}}{\rm{d}}x\).
Câu 14:
Cho hàm số \(y = \sin x - 3\cos x\). Vi phân của hàm số là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn C.
Ta có \({\rm{d}}y = {\left( {\sin x - 3\cos x} \right)^\prime }{\rm{d}}x = \left( {\cos x + 3\sin x} \right){\rm{d}}x\).
Câu 15:
Cho hàm số \[y = {\sin ^2}x\]. Vi phân của hàm số là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn B.
Ta có \({\rm{d}}y = {\rm{d}}\left( {{{\sin }^2}x} \right) = {\left( {{{\sin }^2}x} \right)^\prime }{\rm{d}}x\, = \,\cos x.2\sin x{\rm{d}}x\, = \sin 2x{\rm{d}}x\).
Câu 16:
Vi phân của hàm số \[y = \frac{{\tan \sqrt x }}{{\sqrt x }}\]là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
Ta có \({\rm{dy}} = {\left( {\frac{{\tan \sqrt x }}{{\sqrt x }}} \right)^\prime }{\rm{dx}}\,{\rm{ = }}\frac{{\frac{1}{{2\sqrt x }}.\frac{1}{{{{\cos }^2}\sqrt x }}.\sqrt x - \tan \sqrt x .\frac{1}{{2\sqrt x }}}}{x}{\rm{dx }}\)
\({\rm{ = }}\left( {\frac{1}{2}.\frac{1}{{{{\cos }^2}\sqrt x }} - \frac{{\sin \sqrt x }}{{\cos \sqrt x }}.\frac{1}{{2\sqrt x }}} \right)\frac{1}{x}{\rm{dx = }}\frac{{\sqrt x - \sin \sqrt x \cos \sqrt x }}{{2x\sqrt x .{{\cos }^2}\sqrt x }}.dx\)
\({\rm{ = }}\frac{{2\sqrt x - \sin 2\sqrt x }}{{4x\sqrt x .{{\cos }^2}\sqrt x }}.dx\)
Câu 17:
Hàm số \[y = x\sin x + \cos x\] có vi phân là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn B.
Ta có \[dy = {\left( {x\sin x + \cos x} \right)^\prime }{\rm{d}}x = \left( {\sin x + x\cos x - \sin x} \right){\rm{d}}x = \left( {x\cos x} \right){\rm{d}}x\].
Câu 18:
Hàm số \(y{\rm{ }} = \frac{x}{{{x^2} + 1}}\). Có vi phân là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn A.
Ta có \({\rm{dy}} = {\left( {\frac{x}{{{x^2} + 1}}} \right)^\prime }{\rm{dx}} = \frac{{{x^2} + 1 - 2{x^2}}}{{{{({x^2} + 1)}^2}}} = \frac{{1 - {x^2}}}{{{{({x^2} + 1)}^2}}}dx\).
Câu 19:
Cho hàm số ![]() . Biểu thức nào sau đây là vi phân của hàm số đã cho?
. Biểu thức nào sau đây là vi phân của hàm số đã cho?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn A
![]()
Câu 25:
Hàm số ![]() . Biểu thức 0,01f'(0,01) là số nào?
. Biểu thức 0,01f'(0,01) là số nào?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
Do đó 0,01.f' (0,01) = -90
Câu 27:
Cho hàm số 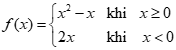 . Kết quả nào dưới đây đúng?
. Kết quả nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Chọn B.
Ta có: ![]() ;
;
![]() và hàm số không có vi phân tại x = 0
và hàm số không có vi phân tại x = 0
Câu 29:
Cho hàm số 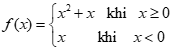 . Khẳng định nào dưới đây là sai?
. Khẳng định nào dưới đây là sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chọn D.
Ta có: ![]() và
và ![]() và d f(0) = dx
và d f(0) = dx