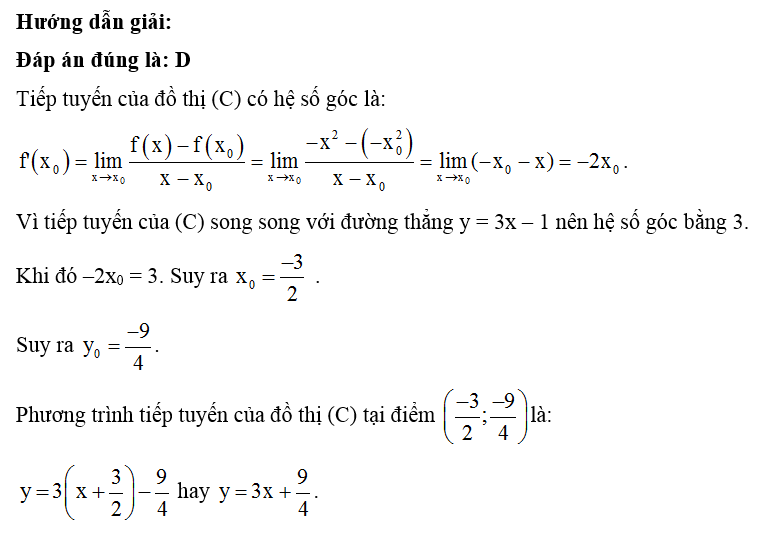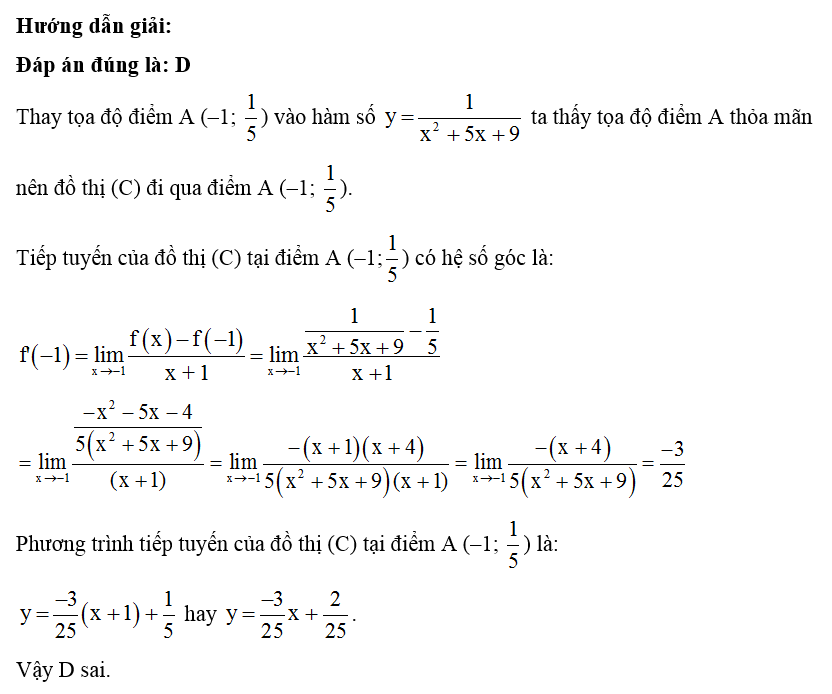10 câu hỏi trắc nghiệm thuộc Dạng 2. Thiết lập phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị

Trắc nghiệm Toán 11 Bài 31. Định nghĩa và ý nghĩa của đạo hàm có đáp án

Dạng 2. Thiết lập phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị

292 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hàm số $y = \frac{x^{2} + 2 x - 3}{x - 2}$ có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm M (3; 12) là:

A. y = 8x + 24;

B. y = 8x – 12;

C. y = 4x – 12;

D. y = – 4x + 24.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Tiếp tuyến của đồ thị (C) tại điểm M(3; 12) có hệ số góc là:

$f' (3) = lim_{x \to 3} \frac{f (x) - f (3)}{x - 3} = \lim_{x \to 3} \frac{\frac{x^{2} + 2 x - 3}{x - 2} - 12}{x - 3} = \lim_{x \to 3} \frac{x - 7}{x - 2} = - 4$ .

Phương trình tiếp tuyến của đồ thị (C) tại điểm M(3; 12) là:

y = – 4(x – 3) + 12 hay y = – 4x + 24.

Câu 2:

Cho hàm số $y = \frac{4x - 5}{7 + x}$ có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm $A (- 1; \frac{- 3}{2})$ là:

A. $y = \frac{11}{12} x + \frac{29}{12}$ ;

B. $y = \frac{11}{12} x - \frac{7}{12}$ ;

C. $y = - \frac{11}{12} x - \frac{7}{12}$ ;

y = - \frac{11}{12} x + \frac{7}{12}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Tiếp tuyến của đồ thị (C) tại điểm $A (- 1; \frac{- 3}{2})$ có hệ số góc là:

$f' (- 1) = lim_{x \to - 1} \frac{f (x) - f (- 1)}{x + 1} = \lim_{x \to - 1} \frac{\frac{4 x - 5}{7 + x} + \frac{3}{2}}{x + 1} = \lim_{x \to - 1} \frac{11}{2 (7 + x)} = \frac{11}{12}$ .

Phương trình tiếp tuyến của đồ thị (C) tại điểm $A (- 1; \frac{- 3}{2})$ là:

$y = \frac{11}{12} (x + 1) - \frac{3}{2}$ hay $y = \frac{11}{12} x - \frac{7}{12}$ .

Câu 3:

Cho hàm số $y = x^{2} - \frac{1}{3} x$ có đồ thị (C), biết hệ số góc của tiếp tuyến tại điểm H có hoành độ bằng 6 là $\frac{35}{3}$ . Phương trình tiếp tuyến của (C) tại điểm H là:

A. $y = \frac{35}{3} x + 34$ ;

B. $y = \frac{35}{3} x - 104$ ;

C. $y = \frac{35}{3} x - 36$ ;

y = \frac{35}{3} x + 38

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Ta có $y (6) = 6^{2} - \frac{1}{3} \cdot 6 = 34$ .

Phương trình tiếp tuyến của đồ thị (C) tại điểm H có hoành độ bằng 6 và hệ số góc bằng $\frac{35}{3}$ là:

$y = \frac{35}{3} (x - 6) + 34$ hay $y = \frac{35}{3} x - 36$ .

Câu 4:

Phương trình tiếp tuyến của hàm số $y = \frac{1 - x}{x - 3}$ (C) tại giao điểm của (C) với trục hoành là:

A. $y = \frac{1}{2} x + \frac{1}{2}$ ;

B. $y = - \frac{1}{2} x + \frac{1}{2}$ ;

C. $y = \frac{1}{2} x - \frac{1}{2}$ ;

y = - \frac{1}{2} x - \frac{1}{2}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Xét phương trình hoành độ giao điểm $\frac{1 - x}{x - 3} = 0$ . Giải phương trình này ta được x = 1.

Suy ra giao điểm của (C) với trục hoành là A(1; 0).

Tiếp tuyến của đồ thị (C) tại điểm A(1; 0) có hệ số góc là:

$f' (1) = lim_{x \to 1} \frac{f (x) - f (1)}{x - 1} = \lim_{x \to 1} \frac{\frac{1 - x}{x - 3}}{x - 1} = \lim_{x \to 1} \frac{1}{3 - x} = \frac{1}{2}$ .

Phương trình tiếp tuyến của đồ thị (C) tại điểm A(1; 0) là:

$y = \frac{1}{2} (x - 1) + 0$ hay $y = \frac{1}{2} x - \frac{1}{2}$ .

Câu 5:

Cho hàm số y = x² + 5x – 6 có đồ thị (C). Phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung là:

A. y = 5x – 6;

B. y = – 6;

C. y = – 6x – 6;

D. y = 5x + 6.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Với x = 0 ta có y = 0² + 5 ∙ 0 – 6 = – 6.

Suy ra giao điểm của (C) với trục tung là A(0; – 6).

Tiếp tuyến của đồ thị (C) tại điểm A(0; – 6) có hệ số góc là:

$f' (0) = lim_{x \to 0} \frac{f (x) - f (0)}{x} = \lim_{x \to 0} \frac{x^{2} + 5 x - 6 + 6}{x} = \lim_{x \to 0} (x + 5) = 5$ .

Phương trình tiếp tuyến của đồ thị (C) tại điểm A(0; –6) là:

y = 5(x – 0) – 6 hay y = 5x – 6.

Câu 6:

Cho hàm số y = – x² có đồ thị (C). Biết phương trình tiếp tuyến của (C) song song với đường thẳng y = 3x – 1, phương trình tiếp tuyến của (C) là:

A. $y = - 3 x - \frac{89}{18}$ ;

B. $y = 3 x + \frac{98}{18}$ ;

C. $y = 3 x - \frac{9}{18}$ ;

y = 3 x + \frac{9}{4}

Xem đáp án

Cho hàm số y = – x^2 có đồ thị (C). Biết phương trình tiếp tuyến của (C) song song với đường thẳng (ảnh 1)

Câu 7:

Cho hàm số y = x³ – 3x² có đồ thị (C). Biết phương trình tiếp tuyến của (C) vuông góc với đường thẳng $y = \frac{1}{2} x + 13$ , phương trình tiếp tuyến của (C) là:

A. $y = - 2 x - \frac{2 \sqrt{3}}{9}$ ;

B. $y = - 2 x+ \frac{2 \sqrt{3}}{9}$ ;

C. Cả A, B đều sai;

D. Cả A, B đều đúng.

Xem đáp án

Cho hàm số y = x^3 – 3x^2 có đồ thị (C). Biết phương trình tiếp tuyến của (C) vuông góc với đường thẳng (ảnh 1)

Câu 8:

Cho hàm số $y = \sqrt{x^{2} - x + 1}$ , có đồ thị (C). Khẳng định nào sau đây là đúng?

A. Phương trình tiếp tuyến của đồ thị (C) tại điểm A(1; 1) là $y = \frac{1}{2} x - \frac{1}{2}$ ;

B. Phương trình tiếp tuyến của đồ thị (C) tại điểm A(1; 1) là $y = \frac{1}{2} x + \frac{1}{2}$ ;

C. Phương trình tiếp tuyến của đồ thị (C) tại điểm A(1; 1) là $y = - \frac{1}{2} x + \frac{1}{2}$ ;

D. Phương trình tiếp tuyến của đồ thị (C) tại điểm A(1; 1) là

y = - \frac{1}{2} x - \frac{1}{2}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Tiếp tuyến của đồ thị (C) tại điểm A (1; 1) có hệ số góc là:

$f' (1) = lim_{x \to 1} \frac{f (x) - f (1)}{x - 1} = \lim_{x \to 1} \frac{\sqrt{x^{2} - x + 1} - 1}{x - 1}$

$= \lim_{x \to 1} \frac{x^{2} - x}{(x - 1) (\sqrt{x^{2} - x + 1} + 1)} = \lim_{x \to 1} \frac{x}{\sqrt{x^{2} - x + 1} + 1} = \frac{1}{2}$

Phương trình tiếp tuyến của đồ thị (C) tại điểm A (1; 1) là:

$y = \frac{1}{2} (x - 1) + 1$ hay $y = \frac{1}{2} x + \frac{1}{2}$ .

Câu 9:

Cho hàm số $y = \frac{1}{x^{2} + 5 x + 9}$ có đồ thị (C). Khẳng định nào sau đây là sai?

A. Đồ thị (C) đi qua điểm A(–1; $\frac{1}{5}$ );

B. Tiếp tuyến của đồ thị (C) tại điểm A(–1; $\frac{1}{5}$ ) có hệ số góc là $\frac{- 3}{25}$ ;

C. Phương trình tiếp tuyến của đồ thị (C) tại điểm A(–1; $\frac{1}{5}$ ) là $y = \frac{- 3}{25} x + \frac{2}{25}$ ;

D. Cả A, B, C đều sai.

Xem đáp án

Cho hàm số y= 1 / x^2 + 5x+ 9 có đồ thị (C). Khẳng định nào sau đây là sai? (ảnh 1)

Câu 10:

Cho hàm số $y = \sqrt{2 x + 1}$ có đồ thị (C). Biết hệ số góc bằng $\frac{1}{3}$ , khi đó phương trình tiếp tuyến của (C) là:

A. $y = \frac{5}{3} x + \frac{1}{3}$ ;

B. $y = \frac{1}{3} x - \frac{5}{3}$ ;

C. $y = - \frac{5}{3} x - \frac{1}{3}$ ;

y = \frac{1}{3} x+ \frac{5}{3}

Xem đáp án

Cho hàm số y= căn bậc hai 2x+ 1 có đồ thị (C). Biết hệ số góc bằng 1/3, khi đó phương trình tiếp tuyến của (C) là: (ảnh 1)

Bắt đầu thi ngay

Trắc nghiệm Toán 11 Bài 31. Định nghĩa và ý nghĩa của đạo hàm có đáp án

Dạng 2. Thiết lập phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương