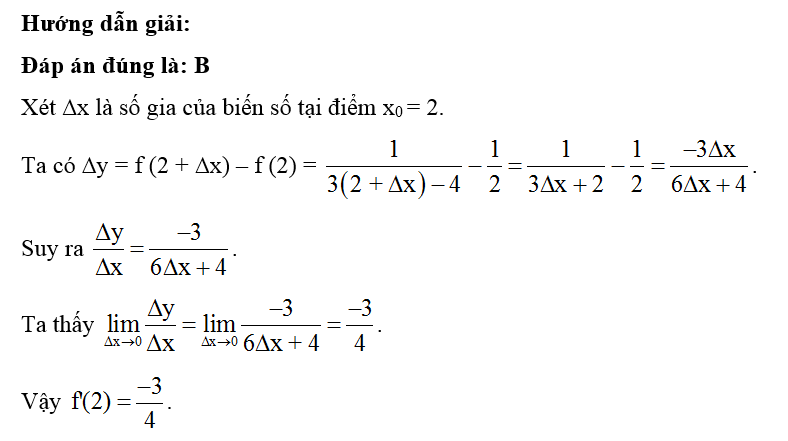10 câu hỏi trắc nghiệm thuộc Dạng 1. Tính đạo hàm bằng định nghĩa (tại một điểm và trên một khoảng)

Trắc nghiệm Toán 11 Bài 31. Định nghĩa và ý nghĩa của đạo hàm có đáp án

Dạng 1. Tính đạo hàm bằng định nghĩa (tại một điểm và trên một khoảng)

293 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hàm số f(x) = 3x² + 2x – 1, ∆x là số gia của biến số tại x₀ = 3. Khi đó ∆y bằng:

A. 3(∆x)² + 20∆x;

B. (∆x)² + 20∆x;

C. 3(∆x)² + 16∆x;

D. 3(∆x)² + 20∆x + 33.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Xét ∆x là số gia của biến số tại điểm x₀= 3.

Ta có ∆y = f(3 + ∆x) – f(3)

= 3(3 + ∆x)² + 2(3 + ∆x) – 1 – (3 ∙ 3² + 2 ∙ 3 – 1)

= 27 + 18∆x + 3(∆x)² + 6 + 2∆x – 33

= 3(∆x)² + 20∆x.

Câu 2:

Đạo hàm của hàm số $f(x) = \frac{1}{3 x - 4}$ tại x₀= 2 là:

A. $\frac{3}{4}$ ;

B. $\frac{- 3}{4}$ ;

C. $\frac{4}{3}$ ;

\frac{- 4}{3}

Xem đáp án

Đạo hàm của hàm số f(x) = 1/ 3x- 4 tại x0 = 2 là: (ảnh 1)

Câu 3:

Cho hàm số $f(x) = \frac{x^{3} - 1}{x + 2}$ . Đạo hàm của số tại x₀= 1 là:

A. 0;

B. 1;

C. –2;

D. 3.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Xét ∆x là số gia của biến số tại điểm x₀= 1.

Ta có ∆y = f(1 + ∆x) – f(1) = $\frac{{(1 + Δ x)}^{3} - 1}{(1 + Δ x) + 2} - 0 = \frac{{(Δ x)}^{3} + 3 Δ x + 3 {(Δ x)}^{2}}{3 + Δ x}$ .

Suy ra $\frac{Δy}{Δx} = \frac{{(Δ x)}^{2} + 3 + 3 Δ x}{Δ x + 3}$ .

Ta thấy $\lim_{Δx \to 0} \frac{Δy}{Δx} = \lim_{Δ x \to 0} \frac{{(Δ x)}^{2} + 3 + 3 Δ x}{Δ x + 3} = 1$ .

Vậy f'(1) = 1.

Câu 4:

Cho hàm số $\sqrt{x - 2}$ , ∆x là số gia của biến số tại x₀ = 3. Khi đó $\frac{Δy}{Δx}$ bằng:

A. $\frac{1 - \sqrt{1 + Δ x}}{Δ x}$ ;

B. $\frac{\sqrt{1 - Δ x} + 1}{Δ x}$ ;

C. $\frac{\sqrt{1 + Δ x} - 1}{Δ x}$ ;

\frac{\sqrt{1 + Δ x} + 1}{Δ x}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Xét ∆x là số gia của biến số tại điểm x₀= 3.

Ta có ∆y = f(3 + ∆x) – f(3) = $\sqrt{3 + Δ x - 2} - 1 = \sqrt{1 + Δ x} - 1$ .

Suy ra $\frac{Δy}{Δx} = \frac{\sqrt{1 + Δ x} - 1}{Δ x}$ .

Câu 5:

Trong các hàm số sau hàm số nào có đạo hàm bằng $\frac{1}{4}$ tại x₀= 1.

A. $\frac{x^{2} - x}{x + 1}$ ;

B. $\frac{x^{2} - 1}{x + 2}$ ;

C. $\frac{x^{2}}{2 - x}$ ;

D. $\frac{x^{2} - 2 x}{x + 1}$ .

Xem đáp án

Trong các hàm số sau hàm số nào có đạo hàm bằng 1/4 tại x0 = 1. (ảnh 1)

Trong các hàm số sau hàm số nào có đạo hàm bằng 1/4 tại x0 = 1. (ảnh 2)

Câu 6:

Cho hàm số f(x) = sin x. Đạo hàm của số tại x₀=

\frac{π}{2}

là:

A. –2;

B. –1;

C. 0;

D. 1.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Xét ∆x là số gia của biến số tại điểm x₀= $\frac{π}{2}$ .

Ta có ∆y = f( $\frac{π}{2}$ + ∆x) – f( $\frac{π}{2}$ ) = sin ( $\frac{π}{2}$ + ∆x) – 1 = cos (∆x) – 1.

Suy ra $\frac{Δy}{Δx} = \frac{\cos (Δ x) - 1}{Δx}$ .

Ta thấy $\lim_{Δx \to 0} \frac{Δy}{Δx} = \lim_{Δ x \to 0} \frac{\cos (Δ x) - 1}{Δx} = 0$ .

Vậy f'( $\frac{π}{2}$ ) = 0.

Câu 7:

Cho hàm số f(x) = $\sqrt{x}$ . Đạo hàm của hàm số tại x₀= 3 là:

A. $\frac{1}{2 \sqrt{3}}$ ;

B. 0;

C. $\frac{1}{\sqrt{3}}$ ;

D. 1.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Xét ∆x là số gia của biến số tại điểm x₀= 3.

Ta có ∆y = f(3 + ∆x) – f(3) = $\sqrt{3 + Δx} - \sqrt{3}$ .

Suy ra $\frac{Δy}{Δx} = \frac{\sqrt{3 + Δ x} - \sqrt{3}}{Δx} = \frac{Δ x}{Δx (\sqrt{3 + Δ x} + \sqrt{3})} = \frac{1}{\sqrt{3 + Δ x} + \sqrt{3}}$ .

Ta thấy $\lim_{Δx \to 0} \frac{Δy}{Δx} = \lim_{Δ x \to 0} \frac{1}{\sqrt{3 + Δ x} + \sqrt{3}} = \frac{1}{2 \sqrt{3}}$ .

Vậy f'(3) = $\frac{1}{2 \sqrt{3}}$ .

Câu 8:

Đạo hàm của hàm số f(x) = x⁴ – 5 tại x₀= 2 là:

A. 8;

B. 24;

C. 0;

D. 32.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Xét ∆x là số gia của biến số tại điểm x₀= 2.

Ta có ∆y = f(2 + ∆x) – f(2) = (2 + ∆x)⁴ – 5 – 11 = (∆x)⁴ + 8(∆x)³ + 24(∆x)² + 32∆x.

Suy ra $\frac{Δy}{Δx} = \frac{{(Δx)}^{4} + 8 {(Δx)}^{3} + 24 {(Δx)}^{2} + 32 Δx}{Δx} = {(Δx)}^{3} + 8 {(Δx)}^{2} + 24 Δx + 32$ .

Ta thấy $\lim_{Δx \to 0} \frac{Δy}{Δx} = \lim_{Δ x \to 0} {(Δx)}^{3} + 8 {(Δx)}^{2} + 24 Δx + 32 = 32$ .

Vậy f'(2) = 32.

Câu 9:

Cho hàm số f(x) = $\sqrt{x - 1}$ . Đạo hàm của hàm số tại x₀= 10 là:

A. –1;

B. 0;

C. $\frac{1}{3}$ ;

\frac{1}{6}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Xét ∆x là số gia của biến số tại điểm x₀= 10.

Ta có ∆y = f(10 + ∆x) – f(10) = $\sqrt{Δx + 9} - 3$ .

Suy ra $\frac{Δy}{Δx} = \frac{\sqrt{Δ x + 9} - 3}{Δx} = \frac{Δ x}{Δx (\sqrt{Δ x + 9} + 3)} = \frac{1}{\sqrt{Δ x + 9} + 3}$ .

Ta thấy $\lim_{Δx \to 0} \frac{Δy}{Δx} = \lim_{Δ x \to 0} = \frac{1}{\sqrt{Δ x + 9} + 3} = \frac{1}{6}$ .

Vậy f'(10) = .

Câu 10:

Đạo hàm của hàm số f(x) = x² – 2x + 1 tại x₀= 1 bằng a. Đạo hàm của hàm số g(x) = x – 2 tại x₀= 4 bằng b. Khi đó a – b bằng:

A. –1;

B. 0;

C. 1;

D. Cả A, B, C đều sai.

Xem đáp án

Đạo hàm của hàm số f(x) = x2 – 2x + 1 tại x0 = 1 bằng a. Đạo hàm của hàm số g(x) = x – 2 tại x0 = 4 bằng b. Khi đó a – b bằng: (ảnh 1)

Bắt đầu thi ngay

Trắc nghiệm Toán 11 Bài 31. Định nghĩa và ý nghĩa của đạo hàm có đáp án

Dạng 1. Tính đạo hàm bằng định nghĩa (tại một điểm và trên một khoảng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương