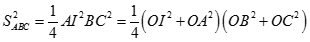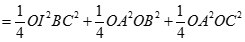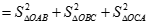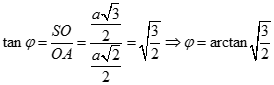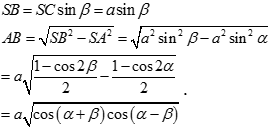Trắc nghiệm Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng có đáp án (Mới nhất)
Dạng 3: Thiết diện và các bài toán liên quan có đáp án
-
300 lượt thi
-
36 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Chọn D
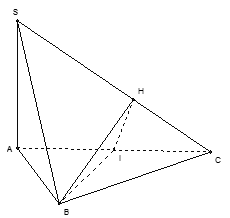
Gọi I là trung điểm của AC, kẻ IH⊥SC
Ta có BI⊥AC, BI⊥SA⇒BI⊥SC
Do đó BI⊥AC, BI⊥SA⇒BI⊥SC hay thiết diện là tam giác BIH
Mà BI⊥(SAC) nên BI⊥IH hay thiết diện là tam giác vuông.
Câu 2:
 Xem đáp án
Xem đáp án
Chọn A
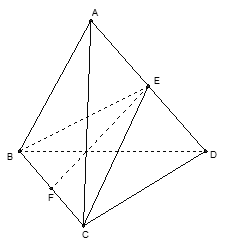
Thiết diện là tam giác BCE, với E là trung điểm của AD. Gọi F là trung điểm của BC
Ta có:
BE=CE=12√32=6√3EF=√BE2−BF2=6√2
Diện tích thiết diện là: S=12EF.BC=36√2
Câu 3:
 Xem đáp án
Xem đáp án
Chọn A
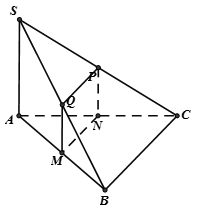
Ta có: {AB⊥BCSA⊥BC⇒BC⊥SB.
Vậy {BC⊥SB(P)⊥SB⇒(P)//BC(1).
Mà (P)∩(ABC)=MN(2).
Từ (1);(2)⇒MN//BC
Tương tự ta có PQ // BC, PN // SA
Mà SA⊥BC⇒PN⊥NM.
Vậy thiết diện là hình thang MNPQ vuông tại N
Câu 4:
 Xem đáp án
Xem đáp án
Chọn A
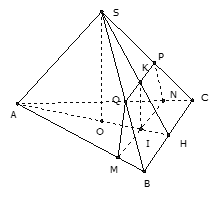
Mặt phẳng (P) vuông góc với OH nên (P) song song với SO
Suy ra (P) cắt (SAH) theo giao tuyến là đường thẳng qua I và song song với SO cắt SH tại K
Từ giả thiết suy ra (P) song song BC, do đó (P) sẽ cắt (ABC), (SBC) lần lượt là các đường thẳng qua I và K song song với BC cắt AB, AC, SB, SC lần lượt tại M, N, P, Q. Do đó thiết diện là tứ giác MNPQ
Ta có MN và PQ cùng song song BC suy ra I là trung điểm của MN và K là trung điểm của PQ
Lại có các tam giác ABC đều và tam giác SBC cân tại S suy ra IK vuông góc với MN và PQ dó đó MNPQ là hình thang cân.
Câu 5:
 Xem đáp án
Xem đáp án
Chọn A
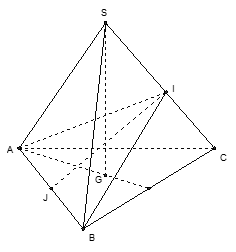
Kẻ AI⊥SC⇒(AIB)⊥SC. Thiết diện là tam giác AIB
Ta có AI=ACsin^ACS=a√1−cos2^ACS=a√1−(a2+b2−b22ab)=a2b√4b2−a2
Gọi J là trung điểm của AB. Dễ thất tam giác AIB cân tại I , suy ra IJ⊥AB
IJ=√AI2−AJ2=a2b√3b2−a2
Do đó: S=12AB.IJ=a2√3b2−a24b
Câu 6:
 Xem đáp án
Xem đáp án
Chọn C
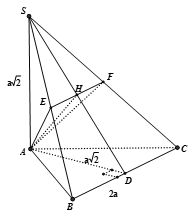
Do AD⊥BC,SA⊥BC⇒BC⊥(SAD)
⇒BC⊥AH⇒EF⊥AH⇒SΔAEF=12EF.AH
Mà EF=12BC=a. Do H là trung điểm SD⇒AH=a⇒SΔAEF=12a2
Câu 7:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh Gọi (P) là mặt phẳng đi qua A và vuông góc với BC. Thiết diện của hình chóp S.ABC được cắt bởi (P) có diện tích bằng?
 Xem đáp án
Xem đáp án
Chọn C
Gọi M là trung điểm của BC thì
Hiển nhiên
Mà
Từ (1) và (2) suy ra
Khi đó thiết diện của hình chóp S.ABC được cắt bởi (P) chính là
vuông tại A nên
Câu 8:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh . Gọi (P) là mặt phẳng đi qua S và vuông góc với BC. Thiết diện của (P) và hình chóp S.ABC có diện tích bằng ?
 Xem đáp án
Xem đáp án
Chọn A
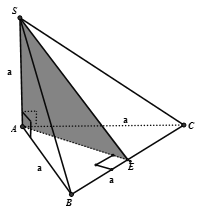
Kẻ
Thiết diện của mặt phẳng (P) và hình chóp (S.ABC) là tam giác SAE có diện tích: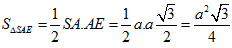
Câu 9:
 Xem đáp án
Xem đáp án
Chọn C
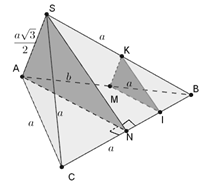
Gọi N là trung điểm của BC
Theo bài ra
Kẻ MI // AN, MK // SA => Thiết diện của (P) và tứ diện SABC là tam giác KMICâu 10:
 Xem đáp án
Xem đáp án
Chọn C
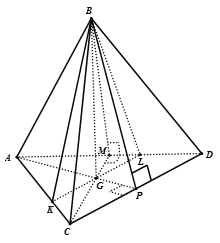
Ta có:
Tương tự:
Suy ra:
Kẻ KL đi qua trọng tâm G của tam giác ACD và song song với CD
=> (P) chính là mặt phẳng (BKL)
Có thể nói nhanh theo tính chất tứ diện đều:
Gọi G là trọng tâm tam giác ACD thì G là tâm tam giác ACD và
Trong mp(ACD) kẻ qua G đường thẳng song song với CD cắt AC, AD lần lượt tại K, L
Ta có . Vậy
Câu 11:
 Xem đáp án
Xem đáp án
Chọn C
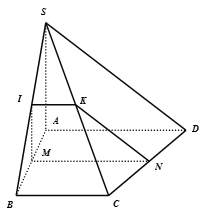
Do
Gọi I là trung điểm của
Gọi N là trung điểm của
Gọi K là trung điểm của , mà
Vậy thiết diện của (P) và hình chóp là hình thang MNKI vuông tại M
Ta có:
MI là đường trung bình của tam giác SAB
IK là đường trung bình của tam giác SBC
MN là đường trung bình của hình thang ABCD
Khi đó
Câu 12:
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Kẻ
a) Khẳng định nào đúng nhất?
 Xem đáp án
Xem đáp án
Chọn A
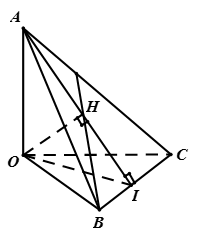
a) Ta có 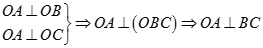
Lại có 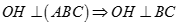
Vậy 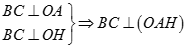
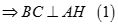
Tương tự
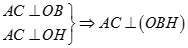
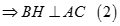
Từ (1) và (2) suy ra H là trực tâm của tam giác ABC
Câu 13:
 Xem đáp án
Xem đáp án
b) Đặt 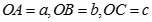
Ta có 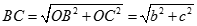
Tương tự 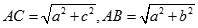
Áp dụng định lí côsin cho tam giác ABC ta có
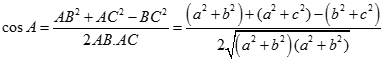
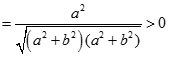 suy ra góc A nhọn.
suy ra góc A nhọn.Tương tự các góc B, C nhọn.
Câu 15:
d) Tìm tập hợp các điểm M trong không gian sao cho 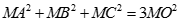
 Xem đáp án
Xem đáp án
Chọn A
d) Gọi I là điểm cách đều 4 điểm O, A, B, C và G là trọng tâm của tam giác ABC thì ta có : 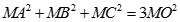
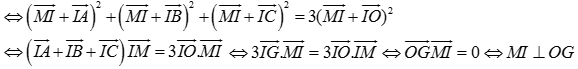
(do 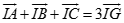 )
)
Vậy M thuộc mặt phẳng đi qua I và vuông góc với OG.
Câu 16:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và SA = a . Gọi I, K lần lượt là trung điểm các cạnh AB và SC. Tính IK.
 Xem đáp án
Xem đáp án
Chọn A
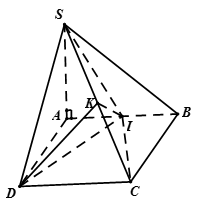
Ta có 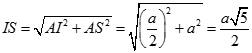
Tương tự 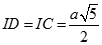 suy ra IS = ID = IC nên I thuộc trục đường tròn ngoại tiếp tam giác SCD
suy ra IS = ID = IC nên I thuộc trục đường tròn ngoại tiếp tam giác SCD
Mặt khác 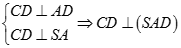
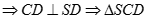 vuông tại D, lại có K là trung điểm của SC nên K là tâm đường tròn ngoại tiếp tam giác SCD, do đó
vuông tại D, lại có K là trung điểm của SC nên K là tâm đường tròn ngoại tiếp tam giác SCD, do đó 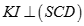
Ta có 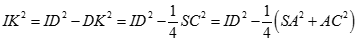
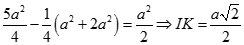
Câu 17:
 Xem đáp án
Xem đáp án
Do 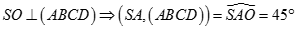
Câu 18:
Cho tứ diện ABCD có DA, DB, DC đôi một vuông góc. Gọi 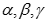 lần lượt là góc giữa các đường thẳng DA, DB, DC với mặt phẳng (ABC)
lần lượt là góc giữa các đường thẳng DA, DB, DC với mặt phẳng (ABC)
Tìm giá trị nhỏ nhất của 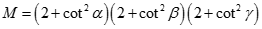
 Xem đáp án
Xem đáp án
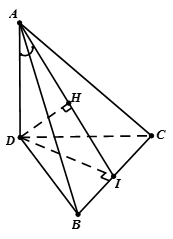
Gọi H là hình chiếu của D trên (ABC)
Khi đó H là trực tâm của tam giác ABC
Và 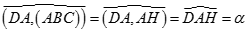
Đặt DA = a, DB = b, DC = c
Gọi thì 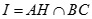 là đường cao của tam giác DBC nên
là đường cao của tam giác DBC nên 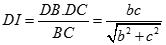
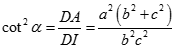
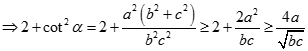
Vậy 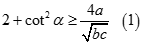
Tương tự 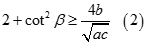 và
và 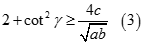
Nhân theo vế các BĐT (1), (2), (3) ta được 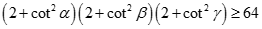 ( đpcm)
( đpcm)
Câu 19:
Trong mặt phẳng cho đường tròn đường kính cố định BC và M là điểm di động trên đường tròn này. Trên đường thẳng d vuông góc với tại B lấy một điểm A.
a) Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn A
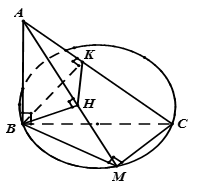
a) Ta có 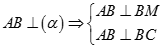 suy ra các tam giác ABM và ABC vuông tại B.
suy ra các tam giác ABM và ABC vuông tại B.
Tiếp theo ta có 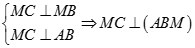
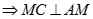 hay tam giác ACM vuông tại M
hay tam giác ACM vuông tại MCâu 20:
 Xem đáp án
Xem đáp án
Chọn D
b) Ta có 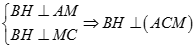
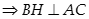
Vậy 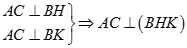
Câu 21:
 Xem đáp án
Xem đáp án
Chọn A
c) Dễ thấy BK cố định và 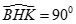 nên điểm H thuộc đường tròn đường kính BK. Từ đó ta có tập hợp các điểm M là đường tròn đường kính BK.
nên điểm H thuộc đường tròn đường kính BK. Từ đó ta có tập hợp các điểm M là đường tròn đường kính BK.
Câu 22:
 Xem đáp án
Xem đáp án
Chọn A
d) 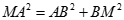 mà AB không đỏi nên AM lớn nhất khi MB lớn nhất
mà AB không đỏi nên AM lớn nhất khi MB lớn nhất 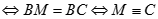
Câu 23:
 Xem đáp án
Xem đáp án
Chọn D
e) Ta có 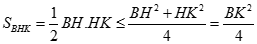 không đổi nên
không đổi nên
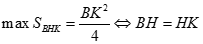 , lúc này vuông cân tại H nên
, lúc này vuông cân tại H nên 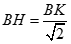
Ta có 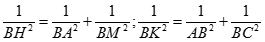
nên 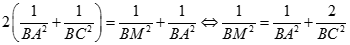
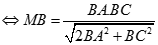
Vậy 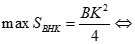
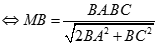 <=> M là các giao điểm của đường tròn đường kính BC với đường tròn tâm B bán kính
<=> M là các giao điểm của đường tròn đường kính BC với đường tròn tâm B bán kính 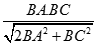
Câu 24:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, BC = , mặt bên SBC là tam giác vuông tại B, mặt bên SCD vuông tại D và SD = a
a) Tính SA.
 Xem đáp án
Xem đáp án
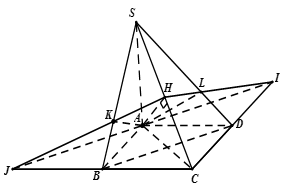
a) 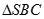 vuông tại
vuông tại 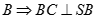 mà
mà 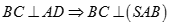
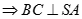
Tương tự ta có 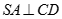 nên
nên 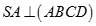
Ta có
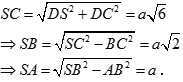
Vậy SA = a
Câu 25:
b) Đường thẳng qua A vuông góc với AC cắt CB, CD lần lượt tại I, J. Gọi H là hình chiếu của A trên SC. Gọi K, L là các giao điểm của SB, SD với (HIJ)
Khẳng định nào sau đây là đúng nhất?
 Xem đáp án
Xem đáp án
Chọn B
b) Do 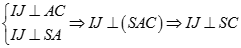
Lại có 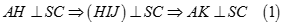
Dế thấy 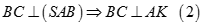
Từ (1), (2) suy ra 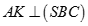
Lập luận tương tự ta có 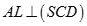
Câu 26:
 Xem đáp án
Xem đáp án
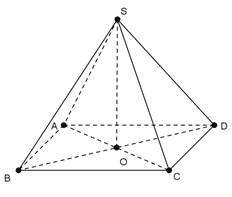
Do 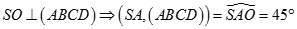
Do đó tam giác SAO vuông cân tại O nên 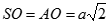
Câu 27:
 Xem đáp án
Xem đáp án
Chọn A
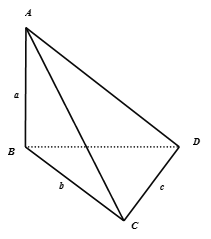
Ta có: 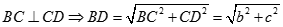
Mặt khác:
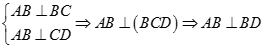
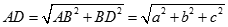
Câu 28:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, 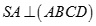 và
và
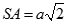 . Giả sử tồn tại tiết diện của hình chóp với mặt phẳng đi qua A vuông góc với SC. Tính diện tích thiết diện.
. Giả sử tồn tại tiết diện của hình chóp với mặt phẳng đi qua A vuông góc với SC. Tính diện tích thiết diện. Xem đáp án
Xem đáp án
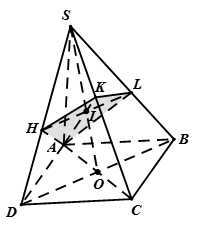
Gọi K là hình chiếu của A trên SC thì 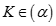 .Trong (SAC) gọi
.Trong (SAC) gọi 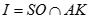
Ta có 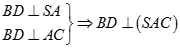
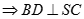 , mặt khác
, mặt khác 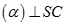 nên
nên 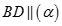
Vậy 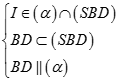
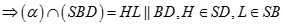
Thiết diện là tứ giác AHKL
Do 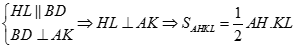
Ta có 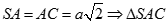 cân tại., mà
cân tại., mà 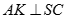 nên K là trung điểm của SC
nên K là trung điểm của SC
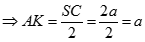
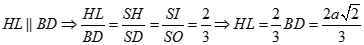
Vậy 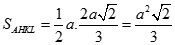
Câu 29:
Cho tam giác ABC tại Ccó cạnh huyền nằm trên mặt phẳng (P) và các cạnh góc vuông tạo với (P) các góc . Giả sử 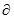 là độ lớn góc giữa đường cao CK với (P). Khẳng định nào sau đây là đúng nhất?
là độ lớn góc giữa đường cao CK với (P). Khẳng định nào sau đây là đúng nhất?
 Xem đáp án
Xem đáp án
Chọn B
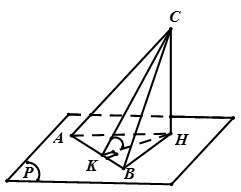
Kẻ 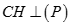 thì
thì 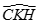 là góc giữa CK và (P) và dễ thấy
là góc giữa CK và (P) và dễ thấy
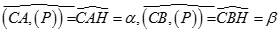
Đặt CH = h, ta có 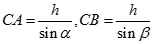
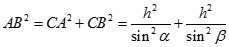
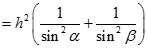
Xét tam giác ABC có CK.AB = CA.CB
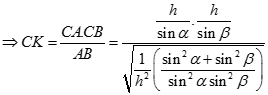
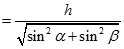
Ta có 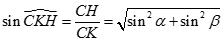
Câu 30:
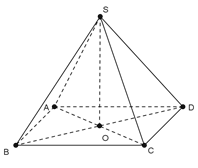
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O, 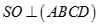 , đường thẳng SA tạo với hai mặt phẳng (ABCD) và (SBC) các góc bằng nhau. Gọi H là hình chiếu của A trên (SBC)
, đường thẳng SA tạo với hai mặt phẳng (ABCD) và (SBC) các góc bằng nhau. Gọi H là hình chiếu của A trên (SBC)
a)Tính SA khi 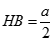
 Xem đáp án
Xem đáp án
Chọn A
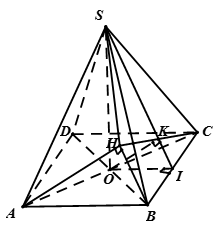
a) Dễ thấy 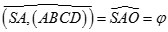 nên
nên 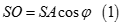
Gọi I là trung điểm của BC thì ta có 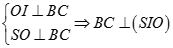
Kẻ 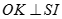 thì
thì 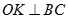 nên
nên 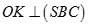
Kẻ 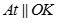 cắt CK tại H, khi đó ta có
cắt CK tại H, khi đó ta có 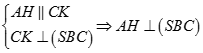 nên
nên 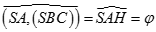 do đó
do đó 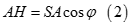
Từ (1), (2) ta có AH = SO
Khi 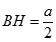 thì trong tam giác vuông HAB có
thì trong tam giác vuông HAB có
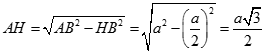
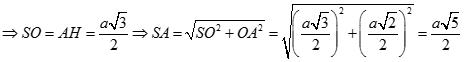
Câu 32:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, 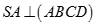 , SC = a. Góc giữa đường thẳng SC với các mặt phẳng (ABCD) và (SAB) lần lượt là
, SC = a. Góc giữa đường thẳng SC với các mặt phẳng (ABCD) và (SAB) lần lượt là 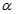 và
và 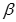
 Xem đáp án
Xem đáp án
Chọn A
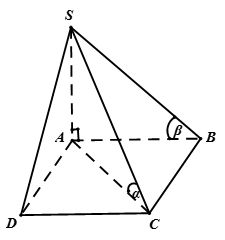
a) Do 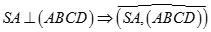
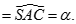
Tương tự 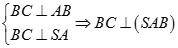
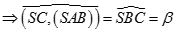
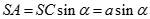
Câu 34:
Cho tứ diện ABCD có 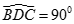 . Hình chiếu H của D trên mặt phẳng ABC là trực tâm tam giác ABC.
. Hình chiếu H của D trên mặt phẳng ABC là trực tâm tam giác ABC.
a) Tính 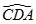
 Xem đáp án
Xem đáp án
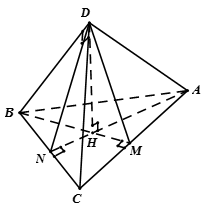
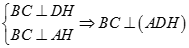
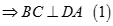
Tương tự ta có 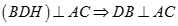 , vì vậy
, vì vậy
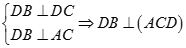
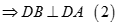
Từ (1), (2) suy ra 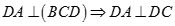 hay
hay 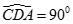
Câu 35:
 Xem đáp án
Xem đáp án
Chọn A
b) Từ câu a) ta thấy tứ diện ABCD có các cạnh DA, DB, DC đôi một vuông góc.
Theo BĐT Cauchy-Schwraz ta có
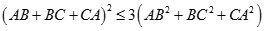
Mà 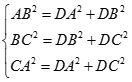 nên
nên 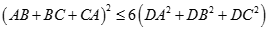
Đẳng thức xảy ra khi 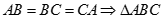 đều, kết hợp với chân đường cao của D trùng với tâm đáy ta được D.ABC là hình chóp đều đỉnh D.
đều, kết hợp với chân đường cao của D trùng với tâm đáy ta được D.ABC là hình chóp đều đỉnh D.
Câu 36:
Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc. M là một điểm bất kì thuộc miền trong tam giác ABC. Tìm giá trị nhỏ nhất của 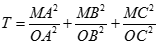
 Xem đáp án
Xem đáp án
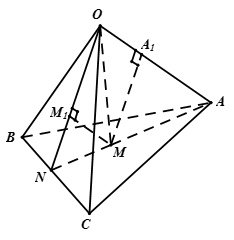
Gọi 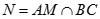 , kẻ
, kẻ 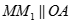
thì ta có
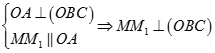
kẻ 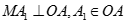 . Khi đó
. Khi đó
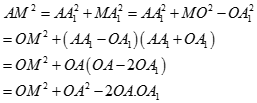
Suy ra 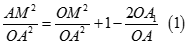
Tương tự gọi B1, C1 là các điểm tương tự như A1 thì ta có
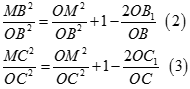
Từ (1), (2), (3) ta có 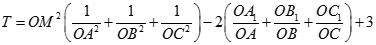
Gọi H là trực tâm của tam giác ABC thì ta đã biết kết quả quen thuộc
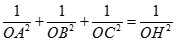 nên
nên 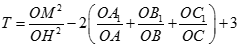
Mặt khác 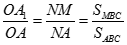
Tương tự 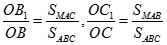 nên
nên 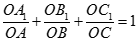
Do đó 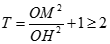 do
do 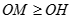
Vậy minT = 2 khi 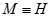
Cách 2. Đặt 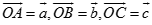 . Do A, B, C, M đồng phẳng nên tồn tại x, y, z sao cho
. Do A, B, C, M đồng phẳng nên tồn tại x, y, z sao cho 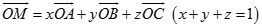
Ta có 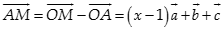 bình phương vô hướng ta được
bình phương vô hướng ta được
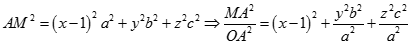
Tương tự 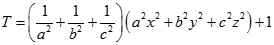
Vì vậy 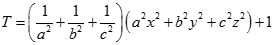
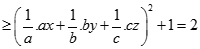 ( Theo Cauchy-Schwarz)
( Theo Cauchy-Schwarz)Vậy minT = 2