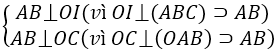Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án
Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án
-
84 lượt thi
-
22 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
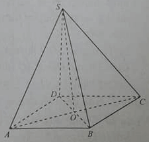
Cho hình chóp S.ABCD, đáy là hình thoi tâm O và SA = SC, SB = SD
Đường thẳng AC vuông góc với mặt phẳng
Xem đáp án
* Xét tam giác SAC có SA = SC nên tam giác cân tại S.
Lại có, SO là đường trung tuyến nên đồng thời là đường cao: (1)
* Vì đáy ABCD là hình thoi nên: (2)
Mà SO và BD là 2 đường thẳng cắt nhau, cùng thuộc mp (SBD) (3)
Từ (1); (2); (3) suy ra:
Đáp án B
Câu 2:
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
Xem đáp án
* Vì ABCD là hình thoi nên (1)
* Xét tam giác SBD có SB = SD nên tam giác SBD cân tại S, có SO là đường trung tuyến nên đồng thời là đường cao: (2)
Mà AC; SO là 2 đường thẳng cắt nhau, cùng nằm trong mp (SAC) (3)
Từ (1) ; (2); (3) suy ra:
Suy ra:
Vì vậy phương án đúng là C.
Câu 3:
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng BC vuông góc với đường thẳng
Xem đáp án
* Xét tam giác SAC có SA = SC nên tam giác cân tại S
Lại có SO là đường trung tuyến nên đồng thời là đường cao:
* Tương tự có:
Mà AC và BD là 2 đường thẳng cắt nhau cùng nằm trong mp(ABCD)
Do đó:
Đáp án D
Câu 4:
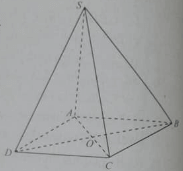
Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD) Tam giác SBC là:
Xem đáp án
Tam giác SBC là tam giác vuông tại B vì : AB là hình chiếu của SB trên (ABCD),
mà BC ⊥ AB (do ABCD là hình vuông)
⇒ BC ⊥ SB (theo định lí ba đường vuông góc)
⇒ tam giác SBC là tam giác vuông
Đáp án D
Câu 5:
Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD) Tam giác SOD là:
Xem đáp án
Tam giác SDO là tam giác vuông tại O vì AO là hình chiếu của SO trên (ABCD) ,
mà DO ⊥ AO (do ABCD là hình vuông)
⇒ DO ⊥ SO (theo định lí ba đường vuông góc)
⇒ tam giác SOD là tam giác vuông.
Đáp án D
Câu 6:
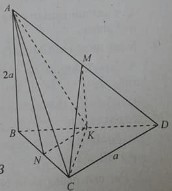
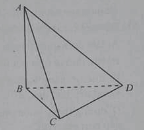
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là:
Xem đáp án
Loại phương án A và B vì BC và CD không phải là hình chiếu của CM trên (BCD)
Phương án C đúng vì :
Đáp án C
Câu 7:
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa CM với mặt phẳng (BCD) bằng:
Xem đáp án
Đáp án A
Câu 8:
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa AC với mặt phẳng (ABD) bằng:
Xem đáp án
* Vì tam giác BCD đều có đường trung tuyến CK nên:
lại có:
Suy ra:
* Do đó, góc (AC; (ABD)) = (AC; AK) =
Đáp án C
Câu 9:
Đường thẳng a vuông góc với hai đường thẳng phân biệt trong mặt phẳng (P) thì:
Xem đáp án
Phương án A sai vì có thể có trường hợp a ⊥ b ⊂ (P); a⊥c ⊂ (P); b // c
Phương án B sai vì có thể xảy ra trường hợp a ⊥ b ⊂ (P); a⊥ c ⊂ (P); b ∩ c ≠ ∅, khi đó a⊥(P).
Đáp án D
Câu 11:
Mệnh đề nào sau đây là đúng?
Xem đáp án
Phương án A sai vì có thể xảy ra trường hợp hai đường thẳng đó vuông góc với nhau
Phương án C sai vì có thể xảy ra trường hợp đường thẳng thuộc mặt phẳng
Phương án D sai vì các đường thẳng đó có thể không đồng phẳng
Đáp án B
Câu 14:
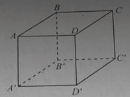
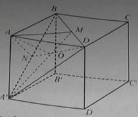
Cho hình lập phương ABCD. A’B’C’D’. AC vuông góc với mặt phẳng.
Xem đáp án
Phương án A sai vì AC không vuông góc với CD ⊂ (CDD’C’)
Phương án B sai vì AC // (A’B’C’D’)
Phương án C đúng vì AC ⊥ BD , AC⊥ BB’ và BD, BB’ ⊂ (BDD’B’)
Đáp án C
Câu 15:
Cho hình lập phương ABCD. A’B’C’D’. Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
Xem đáp án
Gọi M là trung điểm của BD,N là trung điểm của A’B.
Suy ra tâm O của tam giác BDA’ là giao của hai đường trung tuyến DN và A’M. Do đó, O là trọng tâm tam giác A'BD.
Phương án D đúng vì BD ⊥ (AMA') bởi BD ⊥ AM và BD ⊥ A’M ( tam giác A'BD cân tại A' có A'M là đường trung tuyến)
⇒ BD ⊥ AO
BA’ ⊥ (AND) do BA’ ⊥ DN và A’B ⊥ AN ⇒ A’B ⊥ AO
AO ⊥ (A’BD) ⇒ O là hình chiếu của A trên (A’BD).
Đáp án D
Câu 16:
Cho hình tứ diện ABCD có ba cạnh AB, BC, CD đôi một vuông góc.
Đường thẳng AB vuông góc với :
Xem đáp án
AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD
Đáp án A
Câu 17:
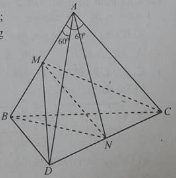
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng . Gọi M, N là trung điểm của AB và CD.
Đường thẳng CD vuông góc với mặt phẳng
Xem đáp án
Ta xét từng phương án:
* Phương án A sai vì nếu CD ⊥ (ABD) thì CD ⊥ AD. Nhưng tam giác ACD cân tại A nên CD không thể vuông góc với AD
* Phương án B sai vì tương tự như trên thì CD không thể vuông góc với AC
* Phương án C đúng vì CD ⊥ AN (AN là đường trung tuyến của tam giác cân CAD tại A)
và CD ⊥ MN ( vì 2 tam giác ABC và ABD bằng nhau ( c.g.c) nên hai đường trung tuyến tương ứng CM = DM.
Tam giác CMD cân tại M có MN là đường trung tuyến)
⇒ CD ⊥ (ABN)
* Phương án D sai vì CD không vuông góc với MD do chứng minh trên.
Đáp án C
Câu 19:
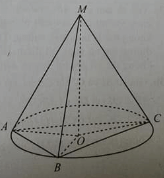
Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là:
Xem đáp án
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, MO là đường thẳng vuông góc với mặt phẳng (ABC) tại O.
Ta có: OA, OB, OC lần lượt là hình chiếu của các đường xiên MA, MB, MC.
Vì OA = OB = OC
⇒ MA = MB = MC.
Vậy đường thẳng MO là tập hợp các điểm cách đều ba đỉnh A, B, C của tam giác ABC.
Đáp án C
Câu 20:
Cho một điểm S có hình chiếu H trên mặt phẳng (P). Với điểm M bất kì trong (P) ta có:
Xem đáp án
Phương án A sai vì khi M trùng với H thì SM = SH
Phương án B đúng vì khi M trùng với H thì SM = SH;
khi M ≠ H thì tam giác SHM là tam giác vuông tại H nên: SM > SH
Phương án C, D sai vì không bao giờ xảy ra trường hợp SM < SH
Đáp án B
Câu 21:
Cho một điểm S có hình chiếu H trên mặt phẳng (P). Với hai điểm M và N trong (P) sao cho SM ≤SN, ta có:
Xem đáp án
Đáp án B
Câu 22:
Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Nếu I là hình chiếu của điểm O trên mặt phẳng (ABC) thì I là:
Xem đáp án
Giả sử AI và CI cắt CB và AB tại K và H
* Vì nên
⇒ AB ⊥ (OCH) ⇒ AB ⊥ CH
Chứng minh tương tự ta cũng có CB ⊥ AK ⇒ I là trực tâm của tam giác ABC
Đáp án B