Câu hỏi:
03/04/2024 29
Cho hình chóp S.ABC có đáy ABC là tam giác đều, O là trung điểm của đường cao AH của tam giác ABC, SO vuông góc với đáy. Gọi I là điểm tùy ý trên OH (không trùng với O và H). mặt phẳng (P) qua I và vuông góc với OH. Thiết diện của (P) và hình chóp S.ABC là hình gì?
A. Hình thang cân
B. Hình thang vuông
C. Hình bình hành
D. Tam giác vuông
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
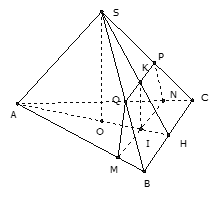
Mặt phẳng (P) vuông góc với OH nên (P) song song với SO
Suy ra (P) cắt (SAH) theo giao tuyến là đường thẳng qua I và song song với SO cắt SH tại K
Từ giả thiết suy ra (P) song song BC, do đó (P) sẽ cắt (ABC), (SBC) lần lượt là các đường thẳng qua I và K song song với BC cắt AB, AC, SB, SC lần lượt tại M, N, P, Q. Do đó thiết diện là tứ giác MNPQ
Ta có MN và PQ cùng song song BC suy ra I là trung điểm của MN và K là trung điểm của PQ
Lại có các tam giác ABC đều và tam giác SBC cân tại S suy ra IK vuông góc với MN và PQ dó đó MNPQ là hình thang cân.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh Gọi (P) là mặt phẳng đi qua A và vuông góc với BC. Thiết diện của hình chóp S.ABC được cắt bởi (P) có diện tích bằng?
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh Gọi (P) là mặt phẳng đi qua A và vuông góc với BC. Thiết diện của hình chóp S.ABC được cắt bởi (P) có diện tích bằng?
Câu 2:
Tam giác ABC có BC = 2a, đường cao . Trên đường thẳng vuông góc với (ABC) tại A, lấy điểm S sao cho . Gọi E, F lần lượt là trung điểm của SB và SC. Diện tích tam giác AEF bằng?
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và SA = a . Gọi I, K lần lượt là trung điểm các cạnh AB và SC. Tính IK.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và SA = a . Gọi I, K lần lượt là trung điểm các cạnh AB và SC. Tính IK.
Câu 4:
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Kẻ
a) Khẳng định nào đúng nhất?
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, 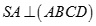 và
và
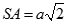 . Giả sử tồn tại tiết diện của hình chóp với mặt phẳng đi qua A vuông góc với SC. Tính diện tích thiết diện.
. Giả sử tồn tại tiết diện của hình chóp với mặt phẳng đi qua A vuông góc với SC. Tính diện tích thiết diện.Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, BC = , mặt bên SBC là tam giác vuông tại B, mặt bên SCD vuông tại D và SD = a
a) Tính SA.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, BC = , mặt bên SBC là tam giác vuông tại B, mặt bên SCD vuông tại D và SD = a
a) Tính SA.
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, 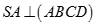 , SC = a. Góc giữa đường thẳng SC với các mặt phẳng (ABCD) và (SAB) lần lượt là
, SC = a. Góc giữa đường thẳng SC với các mặt phẳng (ABCD) và (SAB) lần lượt là 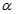 và
và 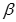
a) Tính SA
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, 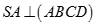 , SC = a. Góc giữa đường thẳng SC với các mặt phẳng (ABCD) và (SAB) lần lượt là
, SC = a. Góc giữa đường thẳng SC với các mặt phẳng (ABCD) và (SAB) lần lượt là 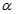 và
và 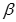
Câu 9:
b) Gọi H, K lần lượt là hình chiếu của B trên AM và AC. Khẳng định nào sau đây là sai?
Câu 10:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O, 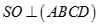 , đường thẳng SA tạo với hai mặt phẳng (ABCD) và (SBC) các góc bằng nhau. Gọi H là hình chiếu của A trên (SBC)
, đường thẳng SA tạo với hai mặt phẳng (ABCD) và (SBC) các góc bằng nhau. Gọi H là hình chiếu của A trên (SBC)
a)Tính SA khi 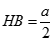
Câu 11:
Cho tam giác ABC tại Ccó cạnh huyền nằm trên mặt phẳng (P) và các cạnh góc vuông tạo với (P) các góc . Giả sử 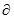 là độ lớn góc giữa đường cao CK với (P). Khẳng định nào sau đây là đúng nhất?
là độ lớn góc giữa đường cao CK với (P). Khẳng định nào sau đây là đúng nhất?
Câu 12:
b) Đường thẳng qua A vuông góc với AC cắt CB, CD lần lượt tại I, J. Gọi H là hình chiếu của A trên SC. Gọi K, L là các giao điểm của SB, SD với (HIJ)
Khẳng định nào sau đây là đúng nhất?
b) Đường thẳng qua A vuông góc với AC cắt CB, CD lần lượt tại I, J. Gọi H là hình chiếu của A trên SC. Gọi K, L là các giao điểm của SB, SD với (HIJ)
Khẳng định nào sau đây là đúng nhất?


