10 câu hỏi trắc nghiệm thuộc Dạng 3: Khoảng cách giữa hai đường thẳng chéo nhau có đáp án

Câu 1:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáy ABCD. Gọi K, H theo thứ tự là hình chiếu vuông góc của A và O lên SD. Chọn khẳng định đúng trong các khẳng định sau?

A. Đoạn vuông góc chung của AC và SD là AK;

B. Đoạn vuông góc chung của AC và SD là CD;

C. Đoạn vuông góc chung của AC và SD là OH;

D. Các khẳng định trên đều sai.

Xem đáp án

Đáp án đúng là: D

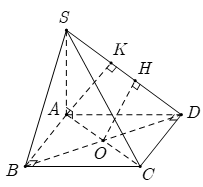
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáy ABCD. (ảnh 1)

Vì SA ^ (ABCD) nên SA ^ AB mà AB ^ AD Þ AB ^ (SAD) Þ AB ^ AK.

Nếu AK ^ AC mà AB ^ AK Þ AK ^ (ABC) Þ AK º SA vì SA ^ (ABC).

Þ SA ^ SD Þ DSAD có hai góc vuông (vô lý). Suy ra đáp án A sai.

Vì ABCD là hình vuông AC và CD không vuông góc với nhau. Do đó đáp án B sai.

Nếu AC ^ OH mà AC ^ BD nên AC ^ (SBD) Þ AC ^ SO

Þ DSOA có hai góc vuông (vô lý).

Do đó đáp án C sai.

Câu 2:

Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa AB và CD.

A. $\frac{a \sqrt{3}}{2}$

B. $\frac{a \sqrt{2}}{3}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a \sqrt{3}}{3}$

Xem đáp án

Đáp án đúng là: C

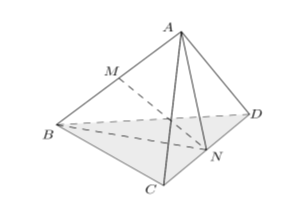
Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa AB và CD. A. ; (ảnh 1)

Gọi M, N lần lượt là trung điểm của AB và CD.

Vì các DACD, DBCD đều nên $A N = B N = \frac{a \sqrt{3}}{2}$ .

Do đó DANB cân tại N, suy ra MN ^ AB

Chứng minh tương tự ta có MN ^ CD, nên d(AB, CD) = MN.

Vì M là trung điểm của AB nên $A M = \frac{A B}{2} = \frac{a}{2}$ .

Xét DAMN vuông tại M, có $M N = \sqrt{A N^{2} - A M^{2}} = \sqrt{\frac{3 a^{2}}{4} - \frac{a^{2}}{4}} = \frac{a \sqrt{2}}{2}$ .

Câu 3:

Cho hình chóp S.ABCD có SA ^ (ABCD), đáy ABCD là hình chữ nhật với $A C = a \sqrt{5}$ và $B C = a \sqrt{2}$ . Tính khoảng cách giữa SD và BC.

A. $\frac{3 a}{4}$

B. $\frac{2 a}{3}$

C. $\frac{a \sqrt{3}}{2}$

D. $a \sqrt{3}$

Xem đáp án

Đáp án đúng là: D

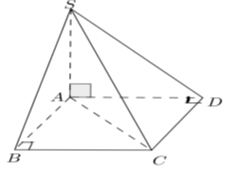
Cho hình chóp S.ABCD có SA  (ABCD), đáy ABCD là hình chữ nhật với (ảnh 1)

Vì SA ^ (ABCD) Þ SA ^ CD mà CD ^ AD Þ CD ^ (SAD) Þ CD ^ SD (1).

Mặt khác BC ^ CD (2).

Từ (1), (2), ta có CD là đoạn vuông góc chung của BC và SD.

Do đó d(BC, SD) = CD = AB (do ABCD là hình chữ nhật).

Xét DABC vuông tại B, có $A B = \sqrt{A C^{2} - B C^{2}} = \sqrt{5 a^{2} - 2 a^{2}} = \sqrt{3} a$ .

Câu 4:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB' và AC bằng:

A. $\frac{a}{2}$

B. $\frac{a}{3}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a \sqrt{3}}{3}$

Xem đáp án

Đáp án đúng là: C

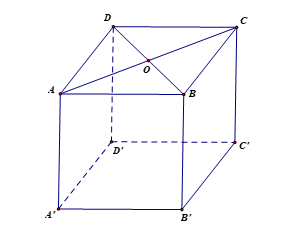
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB' và AC bằng: (ảnh 1)

Gọi O là tâm của hình vuông ABCD nên O là trung điểm của AC, BD.

Vì ABCD là hình vuông nên AC ^ BD tại O.

Do đó BO ^ AC (1).

Mà BB' ^ (ABCD) Þ BB' ^ BO (2).

Từ (1) và (2), ta có BO là đoạn vuông góc chung của AC và BB'.

Do đó d(AC, BB') = BO.

Mà $B O = \frac{1}{2} B D = \frac{1}{2} \sqrt{A B^{2} + A D^{2}} = \frac{a \sqrt{2}}{2}$ .

Do đó d(AC, BB') = $\frac{a \sqrt{2}}{2}$ .

Câu 5:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Khoảng cách giữa AA' và BD' bằng:

A. $\frac{\sqrt{3}}{3}$

B. $\frac{\sqrt{2}}{2}$

C. $\frac{2 \sqrt{2}}{5}$

D. $\frac{3 \sqrt{5}}{7}$

Xem đáp án

Đáp án đúng là: B

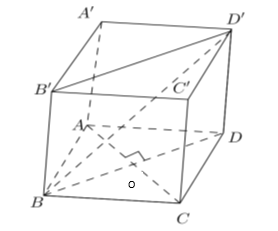
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Khoảng cách giữa AA' và BD' bằng: (ảnh 1)

Vì AA' // BB' nên AA' // (BB'D'D).

Do đó d(AA', BD') = d(AA', (BB'D'D)) = d(A, (BB'D'D)).

Gọi O là tâm hình vuông ABCD.

Vì ABCD là hình vuông nên AO ^ BD mà BB' ^ AO (do BB' ^ (ABCD)).

Suy ra AO ^ (BB'D'D).

Do đó d(A, (BB'D'D)) = AO $= \frac{1}{2} A C = \sqrt{A B^{2} + B C^{2}} = \frac{\sqrt{2}}{2}$ .

Câu 6:

Cho khối lập phương ABCD.A'B'C'D'. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A'C' là:

A. AA';

B. BD;

C. DA';

D. DD'.

Xem đáp án

Đáp án đúng là: A

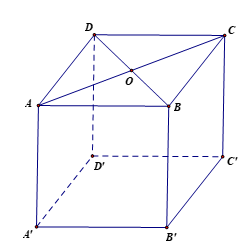
Cho khối lập phương ABCD.A'B'C'D'. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A'C' là: (ảnh 1)

Vì AA' ^ (ABCD) Þ AA' ^ AD.

Vì AA' ^ (A'B'C'D') Þ AA' ^ A'C'.

Do đó AA' là đoạn vuông góc chung của AD và A'C'.

Câu 7:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau?

A. a

B. $a \sqrt{2}$

C. $a \sqrt{3}$

D. 2a

Xem đáp án

Đáp án đúng là: A

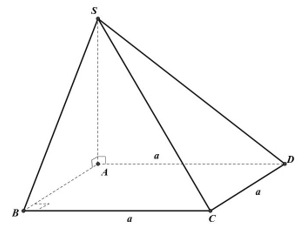
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. (ảnh 1)

Có CD // AB Þ CD // (SAB).

Do đó d(CD, SB) = d(CD, (SAB)) = d(C, (SAB)).

Vì SA ^ (ABCD) Þ SA ^ CB mà CB ^ AB nên CB ^ (SAB).

Do đó d(C, (SAB)) = CB = a.

Câu 8:

Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc với nhau, OA = OB = OC = a. Gọi I là trung điểm BC. Khoảng cách giữa AI và OC bằng bao nhiêu?

A. a

B. $\frac{a}{\sqrt{5}}$

C. $\frac{a \sqrt{3}}{2}$

D. $\frac{a}{2}$

Xem đáp án

Đáp án đúng là: B

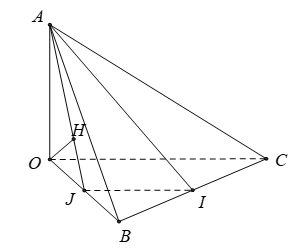
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc với nhau, OA = OB = OC = a. Gọi I là trung điểm BC. Khoảng cách giữa AI và OC bằng bao nhiêu? (ảnh 1)

Gọi J là trung điểm OB. Kẻ OH vuông góc AJ tại H.

Vì J là trung điểm của OB nên $O J = \frac{O B}{2} = \frac{a}{2}$ .

Tam giác AOJ vuông tại O, có OH là đường cao

Ta có: $\frac{1}{O H^{2}} = \frac{1}{O A^{2}} + \frac{1}{O J^{2}} = \frac{1}{a^{2}} + \frac{4}{a^{2}} = \frac{5}{a^{2}} \Rightarrow O H = \frac{a \sqrt{5}}{5}$ .

Vì I, J là trung điểm của BC và OB nên IJ là đường trung bình của DOBC.

Suy ra IJ // OC Þ OC // (AIJ)

Do đó: d(OC, AI) = d(OC, (AIJ)) = d(O, (AIJ)).

Vì IJ // OC mà OC ^ OB nên IJ ^ OB (1).

Vì OA ^ OB và OA ^ OC nên OA ^ (OBC) Þ OA ^ IJ (2).

Từ (1), (2), suy ra IJ ^ (OAB) Þ IJ ^ OH mà OH ^ AJ Þ OH ^ (AIJ).

Do đó d(O, (AIJ)) = OH = $\frac{a \sqrt{5}}{5}$ .

Câu 9:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA vuông góc với mặt đáy và SA = a. Tính khoảng cách giữa SB và CD.

A. $\frac{a \sqrt{2}}{4}$

B. $\frac{a}{2}$

C. $\frac{a \sqrt{3}}{3}$

D. $\frac{a \sqrt{2}}{2}$

Xem đáp án

Đáp án đúng là: C

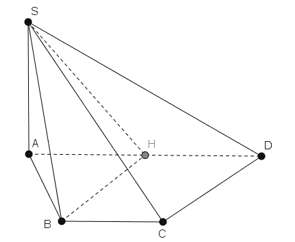
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA vuông góc với mặt đáy và SA = a. (ảnh 1)

Gọi H là trung điểm của AD. Khi đó AH = HD = a.

Vì BC // HD và BC = HD = a nên BCDH là hình bình hành.

Do đó CD // BH Þ CD // (SBH).

Do đó d(SB, CD) = d(CD, (SBH)) = d(D, (SBH)) = d(A, (SBH)).

Gọi h = d(A, (SBH)).

Vì SA, AH, AB đôi một vuông góc với nhau nên ta có :

\frac{1}{h^{2}} = \frac{1}{S A^{2}} + \frac{1}{A H^{2}} + \frac{1}{A B^{2}} = \frac{1}{a^{2}} + \frac{1}{a^{2}} + \frac{1}{a^{2}} = \frac{3}{a^{2}} \Rightarrow h = \frac{a \sqrt{3}}{3}

.

Câu 10:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BD.

A. $\frac{a h}{\sqrt{3 a^{2} + h^{2}}}$

B. $\frac{a h}{\sqrt{a^{2} + h^{2}}}$

C. $\frac{a h}{\sqrt{2 a^{2} + h^{2}}}$

D. $\frac{a h}{\sqrt{a^{2} + 2 h^{2}}}$

Xem đáp án

Đáp án đúng là: D

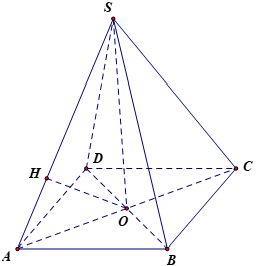
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BD. (ảnh 1)

Gọi O = AC Ç BD. Gọi H là hình chiếu của O lên SA.

Vì S.ABCD là hình chóp đều nên SO ^ (ABCD) Þ SO ^ BD.

Mà AC ^ BD nên BD ^ (SAC) Þ BD ^ OH.

Mà OH ^ SA. Do đó OH là đoạn vuông góc chung của SA và BD.

Suy ra d(SA, BD) = OH.

Xét DABC vuông tại B, ta có $A C = \sqrt{A B^{2} + B C^{2}} = a \sqrt{2}$ .

Lại có O là trung điểm của AC nên $O A = \frac{A C}{2} = \frac{a \sqrt{2}}{2}$ .

Xét DSOA vuông tại O, có $\frac{1}{O H^{2}} = \frac{1}{S O^{2}} + \frac{1}{O A^{2}} = \frac{1}{h^{2}} + \frac{2}{a^{2}} = \frac{a^{2} + 2 h^{2}}{a^{2} h^{2}}$ .

Þ $O H = \frac{a h}{\sqrt{a^{2} + 2 h^{2}}}$ .

Trắc nghiệm Toán 11 Bài 26. Khoảng cách có đáp án

Dạng 3: Khoảng cách giữa hai đường thẳng chéo nhau có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương