20 câu hỏi trắc nghiệm thuộc Dạng 3: Sự biến thiên và đồ thị của hàm số mũ, hàm số lôgarit có đáp án

Câu 1:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Đồ thị hàm số lôgarit nằm bên phải trục tung;

B. Đồ thị hàm số lôgarit nằm bên trái trục tung;

C. Đồ thị hàm số mũ nằm bên phải trục tung;

D. Đồ thị hàm số mũ nằm bên trái trục tung.

Xem đáp án

Đáp án đúng là: A

Vì hàm số lôgarit y = log_ax có tập xác định là (0; +∞) nên đồ thị hàm số luôn nằm bên phải trục tung.

Câu 2:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Đồ thị hàm số lôgarit nằm bên phải trục tung;

B. Đồ thị hàm số lôgarit nằm bên trái trục tung;

C. Đồ thị hàm số mũ nằm bên phải trục tung;

D. Đồ thị hàm số mũ nằm bên trái trục tung.

Xem đáp án

Đáp án đúng là: A

Vì hàm số lôgarit y = log_ax có tập xác định là (0; +∞) nên đồ thị hàm số luôn nằm bên phải trục tung.

Câu 3:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Đồ thị hàm số y = a^x và đồ thị hàm số y = log_ax đối xứng nhau qua đường thẳng y = x;

B. Hàm số y = a^x với 0 < a < 1 đồng biến trên khoảng (-∞; +∞);

C. Hàm số y = a^x với a > 1 nghịch biến trên khoảng (-∞; +∞);

D. Đồ thị hàm số y = a^x với a > 0 và a ≠ 1 luôn đi qua điểm M(a; 1).

Xem đáp án

Đáp án đúng là: A

+ Mệnh đề B sai vì hàm số y = a^x với 0 < a < 1 nghịch biến trên khoảng (-∞; +∞).

+ Mệnh đề C sai vì hàm số y = a^x với a > 1 đồng biến trên khoảng (-∞; +∞).

+ Mệnh đề D sai vì đồ thị hàm số y = a^x với a < 0 và a ≠ 1 luôn đi qua điểm M(a; a^a) hoặc M(0; 1) chứ không phải M(a; 1).

Do đó, chỉ có mệnh đề A là đúng.

Câu 4:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Đồ thị hàm số y = a^x và đồ thị hàm số y = log_ax đối xứng nhau qua đường thẳng y = x;

B. Hàm số y = a^x với 0 < a < 1 đồng biến trên khoảng (-∞; +∞);

C. Hàm số y = a^x với a > 1 nghịch biến trên khoảng (-∞; +∞);

D. Đồ thị hàm số y = a^x với a > 0 và a ≠ 1 luôn đi qua điểm M(a; 1).

Xem đáp án

Đáp án đúng là: A

+ Mệnh đề B sai vì hàm số y = a^x với 0 < a < 1 nghịch biến trên khoảng (-∞; +∞).

+ Mệnh đề C sai vì hàm số y = a^x với a > 1 đồng biến trên khoảng (-∞; +∞).

+ Mệnh đề D sai vì đồ thị hàm số y = a^x với a < 0 và a ≠ 1 luôn đi qua điểm M(a; a^a) hoặc M(0; 1) chứ không phải M(a; 1).

Do đó, chỉ có mệnh đề A là đúng.

Câu 5:

Đối xứng qua trục hoành của đồ thị hàm số y = log₂x là đồ thị nào trong các đồ thị hàm số sau?

A. $y = \log_{\frac{1}{2}} x$

B. y = 2^x;

C. $y = \log_{2} \sqrt{x}$

D. $y = {(\frac{1}{2})}^{x}$

Xem đáp án

Đáp án đúng là: A

Dựa vào lý thuyết Đồ thị hàm số y = f(x) đối xứng qua trục hoành ta được đồ thị hàm số y = -f(x) . Do đó đồ thị hàm số $y = \log_{2} x$ đối xứng qua trục hoành ta được đồ thị hàm số $y = - \log_{2} x .$

Thực hiện phép biến đổi: $y = - \log_{2} x = \log_{\frac{1}{2}} x$ .

Câu 6:

Đối xứng qua trục hoành của đồ thị hàm số y = log₂x là đồ thị nào trong các đồ thị hàm số sau?

A. $y = \log_{\frac{1}{2}} x$

B. y = 2^x;

C. $y = \log_{2} \sqrt{x}$

D. $y = {(\frac{1}{2})}^{x}$

Xem đáp án

Đáp án đúng là: A

Dựa vào lý thuyết Đồ thị hàm số y = f(x) đối xứng qua trục hoành ta được đồ thị hàm số y = -f(x) . Do đó đồ thị hàm số $y = \log_{2} x$ đối xứng qua trục hoành ta được đồ thị hàm số $y = - \log_{2} x .$

Thực hiện phép biến đổi: $y = - \log_{2} x = \log_{\frac{1}{2}} x$ .

Câu 7:

Hàm số nào sau đây đồng biến trên khoảng (0; +∞)?

A. $y = \log_{\frac{\sqrt{2}}{2}} x$

B. $y = \log_{\frac{e}{3}} x$

C. $y = \log_{\frac{e}{2}} x$

D. $y = \log_{\frac{π}{4}} x$

Xem đáp án

Đáp án đúng là: C

Áp dụng lý thuyết:

“Hàm số y = log_ax đồng biến khi a > 1, nghịch biến khi 0 < a < 1”.

Trong các hàm số đã cho chỉ có hàm số đồng biến vì cơ số $a = \frac{e}{2} > 1$ .

Câu 8:

Hàm số nào sau đây đồng biến trên khoảng (0; +∞)?

A. $y = \log_{\frac{\sqrt{2}}{2}} x$

B. $y = \log_{\frac{e}{3}} x$

C. $y = \log_{\frac{e}{2}} x$

D. $y = \log_{\frac{π}{4}} x$

Xem đáp án

Đáp án đúng là: C

Áp dụng lý thuyết:

“Hàm số y = log_ax đồng biến khi a > 1, nghịch biến khi 0 < a < 1”.

Trong các hàm số đã cho chỉ có hàm số đồng biến vì cơ số $a = \frac{e}{2} > 1$ .

Câu 9:

Điều kiện của a để hàm số y = (2a - 5)^x nghịch biến trên ℝ là:

A. $\frac{5}{2} < a < 3$

B. $\frac{5}{2} \leq a \leq 3$

C. $a > 3;$

$D . a < \frac{5}{2}$

Xem đáp án

Đáp án đúng là: A

Hàm số y = (2a - 5)^x nghịch biến trên ℝ khi 0 < 2a - 5 < 1 ⇔ $\frac{5}{2} < a < 3$ .

Câu 10:

Điều kiện của a để hàm số y = (2a - 5)^x nghịch biến trên ℝ là:

A. $\frac{5}{2} < a < 3$

B. $\frac{5}{2} \leq a \leq 3$

C. $a > 3;$

$D . a < \frac{5}{2}$

Xem đáp án

Đáp án đúng là: A

Hàm số y = (2a - 5)^x nghịch biến trên ℝ khi 0 < 2a - 5 < 1 ⇔ $\frac{5}{2} < a < 3$ .

Câu 11:

Tìm tất cả các giá trị của tham số để hàm số đồng biến.

A. a = 1;

B. a = 2;

C. a Î (1; 2);

D. a Î (-∞; 1) È (2; +∞).

Xem đáp án

Đáp án đúng là: D

Điều kiện để hàm số đồng biến là:

$a^{2} - 3 a + 3 > 1 \Leftrightarrow a^{2} - 3 a + 2 > 0 \Leftrightarrow [\begin{array}{l} a < 1 \\ a > 2 \end{array}$

Vậy a Î (-∞; 1) È (2; +∞).

Câu 12:

Tìm tất cả các giá trị của tham số để hàm số đồng biến.

A. a = 1;

B. a = 2;

C. a Î (1; 2);

D. a Î (-∞; 1) È (2; +∞).

Xem đáp án

Đáp án đúng là: D

Điều kiện để hàm số đồng biến là:

$a^{2} - 3 a + 3 > 1 \Leftrightarrow a^{2} - 3 a + 2 > 0 \Leftrightarrow [\begin{array}{l} a < 1 \\ a > 2 \end{array}$

Vậy a Î (-∞; 1) È (2; +∞).

Câu 13:

Trong các hàm số sau, hàm số đồng biến trên ℝ?

A. $y = {(\frac{3}{π})}^{x}$

B. $y = {(\frac{\sqrt{2} + \sqrt{3}}{3})}^{x}$

C. $y = {(\frac{\sqrt{3}}{2})}^{x}$

D. $y = {(\frac{π}{\sqrt{2} + \sqrt{3}})}^{x}$

Xem đáp án

Đáp án đúng là: B

Áp dụng lý thuyết: “Hàm số y = a^x đồng biến khi a > 1, nghịch biến khi 0 < a < 1.”

Trong các hàm số đã cho chỉ có hàm số $y = {(\frac{\sqrt{2} + \sqrt{3}}{3})}^{x}$ đồng biến vì cơ số $a = \frac{\sqrt{2} + \sqrt{3}}{3} > 1$ .

Câu 14:

Trong các hàm số sau, hàm số đồng biến trên ℝ?

A. $y = {(\frac{3}{π})}^{x}$

B. $y = {(\frac{\sqrt{2} + \sqrt{3}}{3})}^{x}$

C. $y = {(\frac{\sqrt{3}}{2})}^{x}$

D. $y = {(\frac{π}{\sqrt{2} + \sqrt{3}})}^{x}$

Xem đáp án

Đáp án đúng là: B

Áp dụng lý thuyết: “Hàm số y = a^x đồng biến khi a > 1, nghịch biến khi 0 < a < 1.”

Trong các hàm số đã cho chỉ có hàm số $y = {(\frac{\sqrt{2} + \sqrt{3}}{3})}^{x}$ đồng biến vì cơ số $a = \frac{\sqrt{2} + \sqrt{3}}{3} > 1$ .

Câu 15:

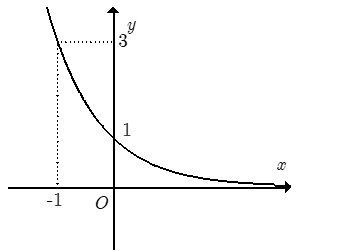
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. (ảnh 1)

A. $y = {(\sqrt{3})}^{x}$

B. $y = {(\frac{1}{2})}^{x}$

C. $y = 2^{x} + \frac{5}{2}$

D. $y = {(\frac{1}{3})}^{x}$

Xem đáp án

Đáp án đúng là: D

Dựa vào hình dáng đồ thị từ trái sang phải ta thấy: x tăng nhưng y giảm. Suy ra hàm số tương ứng của đồ thị là hàm nghịch biến. Loại A, C.

Đồ thị hàm số đi qua điểm có tọa độ (-1; 3) nên chỉ có D thỏa mãn.

Câu 16:

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. $y = {(\sqrt{3})}^{x}$

B. $y = {(\frac{1}{2})}^{x}$

C. $y = 2^{x} + \frac{5}{2}$

D. $y = {(\frac{1}{3})}^{x}$

Xem đáp án

Đáp án đúng là: D

Dựa vào hình dáng đồ thị từ trái sang phải ta thấy: x tăng nhưng y giảm. Suy ra hàm số tương ứng của đồ thị là hàm nghịch biến. Loại A, C.

Đồ thị hàm số đi qua điểm có tọa độ (-1; 3) nên chỉ có D thỏa mãn.

Câu 17:

Cho a, b, c là các số thực dương khác 1. Hình vẽ dưới đây là đồ thị của ba hàm số

y = a^x, y = b^x, y = c^x.

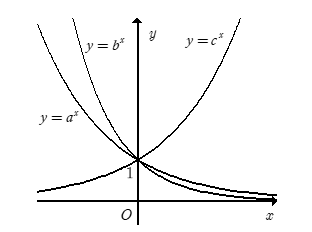
Khẳng định nào sau đây là đúng?

A. a > b > c;

B. a < b < c;

C. c > a > b;

D. a > c > b.

Xem đáp án

Đáp án đúng là: C

Ta thấy hàm y = c^x có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến suy ra c > 1.

Hàm số y = a^x và y = b^x là những hàm số nghịch biến y = a^x và y = b^x là những hàm nghịch biến suy ra a, b < 1. Từ đó loại được các đáp án A, D.

Từ đồ thị hàm số ta thấy tại cùng một giá trị x₀ < 0 thì đồ thị hàm số y = b^x nằm trên đồ thị hàm số y = a^x hay $\{\begin{cases} x < 0 \\ b^{x} > a^{x} \end{cases} \Rightarrow b < a$ .

Vây c > a > b.

Câu 18:

Cho a, b, c là các số thực dương khác 1. Hình vẽ dưới đây là đồ thị của ba hàm số

y = a^x, y = b^x, y = c^x.

Khẳng định nào sau đây là đúng?

A. a > b > c;

B. a < b < c;

C. c > a > b;

D. a > c > b.

Xem đáp án

Đáp án đúng là: C

Ta thấy hàm y = c^x có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến suy ra c > 1.

Hàm số y = a^x và y = b^x là những hàm số nghịch biến y = a^x và y = b^x là những hàm nghịch biến suy ra a, b < 1. Từ đó loại được các đáp án A, D.

Từ đồ thị hàm số ta thấy tại cùng một giá trị x₀ < 0 thì đồ thị hàm số y = b^x nằm trên đồ thị hàm số y = a^x hay $\{\begin{cases} x < 0 \\ b^{x} > a^{x} \end{cases} \Rightarrow b < a$ .

Vây c > a > b.

Câu 19:

Cho a, b, c là các số thực dương khác 1. Hình vẽ dưới đây là đồ thị của ba hàm số

y = log_ax, y = log_bx, y = log_cx.

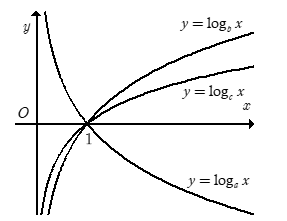
Khẳng định nào sau đây là đúng?

A. a < c < b;

B. a < b < c;

C. b < a < c;

D. b > a > c.

Xem đáp án

Đáp án đúng là: B

Ta thấy hàm y = log_ax có đồ thị từ trái sang phải theo hướng đi xuống nên là hàm nghịch biến suy ra 0 < a < 1.

Còn hàm số y = log_bx và y = log_cx là những hàm đồng biến suy ra b, c > 1. Từ đó loại được các đáp án C, D.

Từ đồ thị hàm số ta thấy tại cùng một giá trị x > 1 thì đồ thị hàm số y = log_bx nằm trên đồ thị hàm số y = log_bx hay $\{\begin{cases} x > 1 \\ \log_{b} x > \log_{c} x \end{cases} \Rightarrow b < c$ .

Vậy a < b < c.

Câu 20:

Cho a, b, c là các số thực dương khác 1. Hình vẽ dưới đây là đồ thị của ba hàm số

y = log_ax, y = log_bx, y = log_cx.

Khẳng định nào sau đây là đúng?

A. a < c < b;

B. a < b < c;

C. b < a < c;

D. b > a > c.

Xem đáp án

Đáp án đúng là: B

Ta thấy hàm y = log_ax có đồ thị từ trái sang phải theo hướng đi xuống nên là hàm nghịch biến suy ra 0 < a < 1.

Còn hàm số y = log_bx và y = log_cx là những hàm đồng biến suy ra b, c > 1. Từ đó loại được các đáp án C, D.

Từ đồ thị hàm số ta thấy tại cùng một giá trị x > 1 thì đồ thị hàm số y = log_bx nằm trên đồ thị hàm số y = log_bx hay $\{\begin{cases} x > 1 \\ \log_{b} x > \log_{c} x \end{cases} \Rightarrow b < c$ .

Vậy a < b < c.

Trắc nghiệm Toán 11 Bài 20. Hàm số mũ và hàm số lôgarit có đáp án

Dạng 3: Sự biến thiên và đồ thị của hàm số mũ, hàm số lôgarit có đáp án

Danh sách câu hỏi

$D . a < \frac{5}{2}$

$D . a < \frac{5}{2}$

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương

Trắc nghiệm Toán 11 Bài 20. Hàm số mũ và hàm số lôgarit có đáp án

Dạng 3: Sự biến thiên và đồ thị của hàm số mũ, hàm số lôgarit có đáp án

Danh sách câu hỏi

D. a<52

D. a<52

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương

$D . a < \frac{5}{2}$

$D . a < \frac{5}{2}$