10 câu hỏi trắc nghiệm thuộc Dạng 1: Xác định hợp và giao của hai tập hợp có đáp án

Câu 1:

Cho các tập hợp:

A = {x ∈ ℤ | – 5 < x < 6};

B = {x ∈ ℤ | 1 < x < 6}.

Xác định tập hợp X = A ∩ B.

A. X = {2; 3; 4};

B. X = {2; 3; 4; 5};

C. X = {3; 4; 5};

D. X = {1; 2; 3; 4}.

Xem đáp án

Đáp án đúng là: B.

Ta có:

+ Tập hợp A gồm các phần tử là – 4; – 3; – 2; – 1; 0; 1; 2; 3; 4; 5.

⇒ A = {– 4; – 3; – 2; – 1; 0; 1; 2; 3; 4; 5}.

+ Tập hợp B gồm phần tử là 2; 3; 4; 5.

⇒ B = {2; 3; 4; 5}.

Vì giao của hai tập hợp là các phần tử thuộc tập hợp này cũng là phần tử thuộc tập hợp kia nên tập hợp B gồm có các phần tử là 2; 3; 4; 5.

Vậy X = {2; 3; 4; 5}.

Câu 2:

Cho hai tập hợp:

X = {x ∈ ℕ | 0 ≤ x ≤ 5}

Y là tập hợp các ước số tự nhiên của 15.

X ∩ Y là tập hợp nào dưới đây?

A. A = {1; 2; 3; 4; 5};

B. B = {1; 2; 3};

C. C = {3; 4; 5};

D. D = {1; 3; 5}.

Xem đáp án

Đáp án đúng là: D.

Ta có:

+ Các phần tử của tập hợp X là 0; 1; 2; 3; 4; 5.

Do đó, X = {0; 1; 2; 3; 4; 5}.

+ Các ước số tự nhiên của 15 là 1; 3; 5; 15.

Do đó, Y = {1; 3; 5; 15}.

Vì giao của hai tập hợp là các phần tử thuộc tập hợp này cũng là phần tử thuộc tập hợp kia nên tập hợp X ∩ Y gồm có các phần tử là 1; 3; 5.

Vậy X ∩ Y = {1; 3; 5}.

Câu 3:

Xác định tập hợp A = (1; 4) ∪ (3; 5).

A. A = (1; 5);

B. B = (2; 4);

C. C = (1; 4);

D. D = (2; 5).

Xem đáp án

Đáp án đúng là: A.

Hợp của hai tập hợp trên là các phần tử thuộc tập hợp này hoặc tập hợp kia nên

A = (1; 4) ∪ (3; 5) = (1; 5).

Câu 4:

Cho hai tập hợp sau:

M là tập hợp các số tự nhiên chẵn lớn hơn 0 và bé hơn 10.

N là tập hợp ba số nguyên tố đầu tiên.

M ∪ N là tập hợp nào dưới đây?

A. A = {2; 4; 6; 8};

B. B = {1; 2; 3};

C. C = {0; 2; 4; 6; 8; 10};

D. D = {2; 3; 4; 5; 6; 8}.

Xem đáp án

Đáp án đúng là: D.

Ta có:

+ Các số tự nhiên chẵn lớn hơn 0 và bé hơn 10 là: 2; 4; 6; 8.

⇒ M = {2; 4; 6; 8}.

+ Ba số nguyên tố đầu tiên là 2; 3; 5.

⇒ N = {2; 3; 5}.

Hợp của hai tập hợp M và N là các phần tử thuộc tập hợp M hoặc tập hợp N nên ta có tập hợp M ∪ N gồm có các phần tử là: 2; 3; 4; 5; 6; 8.

Vậy M ∪ N = {2; 3; 4; 5; 6; 8}.

Câu 5:

Cho các tập hợp:

A = {x ∈ ℤ | 1 ≤ x ≤ 4};

B = {x ∈ ℤ | 2 < x < 7}.

Xác định tập hợp X = A ∩ B.

A. X = {1; 2; 3; 4};

B. X = {3; 4; 5; 6};

C. X = {3; 4};

D. X = {4; 5}.

Xem đáp án

Đáp án đúng là: C.

Ta có:

+ Tập hợp A gồm các phần tử là 1; 2; 3; 4.

⇒ A = {1; 2; 3; 4}.

+ Tập hợp B gồm phần tử là 3; 4; 5; 6.

⇒ B = {3; 4; 5; 6}.

Vì giao của hai tập hợp là các phần tử thuộc tập hợp này cũng là phần tử thuộc tập hợp kia nên tập hợp A gồm có các phần tử là {3; 4}.

Vậy X = {3; 4}.

Câu 6:

Cho các tập hợp:

A = {x ∈ ℤ | 5 < x < 8};

B = {x ∈ ℤ | 8 < x < 11}.

Xác định tập hợp X = A ∩ B.

A. X = {6; 7};

B. X = {8; 9};

C. X = {9; 10};

D. X = ∅.

Xem đáp án

Đáp án đúng là: D.

Ta có:

+ Tập hợp A gồm các phần tử là 6; 7.

⇒ A = {6; 7}.

+ Tập hợp B gồm phần tử là 9; 10.

⇒ B = {9; 10}.

Ta có giao của hai tập hợp là các phần tử thuộc tập hợp này cũng là phần tử thuộc tập hợp kia.

Mà hai tập hợp trên không có phần tử nào chung nên tập hợp X không có phần tử nào.

Vậy X = ∅.

Câu 7:

Cho hai tập hợp:

A = {x ∈ ℤ | x(x² – 1) = 0}

B = {x ∈ ℕ | 2 < x < 5}

Câu nào sau đây đúng?

A. A ∪ B = {1; 2; 3; 4};

B. A ∪ B = {–1; 0; 1; 3; 4};

C. A ∪ B = {–1; 0; 1; 2; 3}

D. A ∪ B = {2; 3; 4; 5}.

Xem đáp án

Đáp án đúng là: B.

– Xét tập hợp A ta có:

x(x² – 1) = 0 ⇔ $[\begin{matrix} x = 0 \\ x^{2} - 1 = 0 \end{matrix}$ ⇔ $[\begin{matrix} x = 0 \\ x = - 1 \\ x = 1 \end{matrix}$ .

Vì x ∈ ℤ nên ba nghiệm trên đều thỏa mãn tập hợp A.

Do đó, A = {–1; 0; 1}.

– Tập hợp B gồm có các phần tử là 3; 4.

Do đó, B = {3; 4}.

Hợp của hai tập hợp A và B là các phần tử thuộc tập hợp A hoặc tập hợp B nên ta có tập hợp A ∪ B gồm có các phần tử là –1; 0; 1; 3; 4.

Vậy A ∪ B = {–1; 0; 1; 3; 4}.

Câu 8:

Cho tập hợp H = [1; 7] ∩ (– 3; 5). Đáp án nào sau đây là đúng.

A. H = [1; 7];

B. H = (– 3; 5);

C. H = [1; 5] ;

D. H = [1; 5).

Xem đáp án

Đáp án đúng là: D.

Ta biểu diễn đoạn [1; 7] và khoảng (– 3; 5) lên cùng một trục số, giao của hai tập này chính là phần không bị gạch chéo trên hình sau. Chú ý các điểm đặc biệt ở mút 1 và 5.

Vậy H = [1; 7] ∩ (– 3; 5) = [1; 5).

Câu 9:

Cho hai tập hợp:

A = {x ∈ ℤ | x² – 9 = 0}

B = {x ∈ ℤ | x² + 6x + 5 = 0}

Câu nào sau đây đúng?

A. A ∪ B = {–3; 3};

B. A ∪ B = {–5; –1};

C. A ∪ B = {–5; –3; –1};

D. A ∪ B = {–5; –3; –1; 3}.

Xem đáp án

Đáp án đúng là: D.

– Xét tập hợp A ta có:

x² – 9 = 0 ⇔ $[\begin{matrix} x = - 3 \\ x = 3 \end{matrix}$ .

Vì x ∈ ℤ nên hai nghiệm trên đều thỏa mãn tập hợp A.

⇒ A = {–3; 3}.

– Xét tập hợp B ta có:

x² + 6x + 5 = 0 ⇔ $[\begin{matrix} x = - 1 \\ x = - 5 \end{matrix}$ .

Vì x ∈ ℤ nên hai nghiệm trên đều thỏa mãn tập hợp B.

Do đó, B = {– 1; – 5}.

Hợp của hai tập hợp A và B là các phần tử thuộc tập hợp A hoặc tập hợp B nên ta có tập hợp A ∪ B gồm có các phần tử là –5; –3; –1; 3.

Vậy A ∪ B = {–5; –3; –1; 3}.

Câu 10:

Cho tập hợp H = [1; 7) ∪ (– 3; 5). Đáp án nào sau đây là đúng.

A. H = [1; 7];

B. H = (– 3; 7);

C. H = [1; 5] ;

D. H = [1; 5).

Xem đáp án

Đáp án đúng là: B.

Ta biểu diễn nửa khoảng [1; 7) và khoảng (– 3; 5) lên cùng một trục số, hợp của hai tập này chính là phần được tô đậm và không bị gạch chéo trên hình sau.

Chú ý các điểm đặc biệt ở mút – 3 và 7.

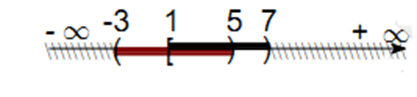
Cho tập hợp H = [1; 7) hợp (– 3; 5). Đáp án nào sau đây là đúng. (ảnh 1)

Vậy H = [1; 7) ∪ (– 3; 5) = (– 3; 7).

Trắc nghiệm Toán 10 CTST Bài 3: Các phép toán trên tập hợp có đáp án

Dạng 1: Xác định hợp và giao của hai tập hợp có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương