Trắc nghiệm Toán 10 Bài tập cuối chương 7 có đáp án
Trắc nghiệm Toán 10 Bài tập cuối chương 7 có đáp án
-
127 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho f(x) = x2 – 4. Tìm khẳng định sai trong các khẳng định sau đây
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét f(x) = x2 – 4 có ∆ = 16 > 0, hai nghiệm phân biệt là x = –2; x = 2 và a = 1 > 0
Ta có bảng xét dấu
|
x |
-∞ – 2 2 +∞ |
|
f(x) |
+ 0 – 0 + |
Từ bảng xét dấu ta có f(x) > với mọi x \( \in \) (- ∞; - 2) và (2; + ∞); f(x) < 0 khi x \[ \in \](– 2; 2)
Vậy khẳng định sai là D.
Câu 2:
Tam thức f(x) = x2 + 2x – 3 nhận giá trị dương khi và chỉ khi
 Xem đáp án
Xem đáp án
Xét f(x) = x2 + 2x – 3 có ∆ = 16 > 0, hai nghiệm phân biệt là x = 1 ; x = – 3 và a = 1 > 0.
Ta có bảng xét dấu
|
x |
–∞ – 3 1 +∞ |
|
f(x) |
+ 0 – 0 + |
Từ bảng xét dấu ta có f(x) > với mọi x \( \in \) (- ∞; - 3) ∪ (1; + ∞); f(x) < 0 khi x \[ \in \](– 3; 1).
Vậy f(x) nhận giá trị dương với mọi x \( \in \) (- ∞; - 3) ∪ (1; + ∞).
Câu 3:
nghiệm của phương trình \[\sqrt {2x - 3} = x - 3\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bình phương hai vế của phương trình ta có
2x – 3 = (x – 3)2
\( \Rightarrow \)2x – 3 = x2 – 6x + 9
\( \Rightarrow \) x2 – 8x + 12 = 0
\( \Rightarrow \) x = 2 hoặc x = 6
Thay lần lượt hai nghiệm vào phương trình, ta thấy x = 6 thoả mãn
Vậy phương trình có 1 nghiệm
Câu 4:
Nghiệm của phương trình \[\sqrt {{x^2} - 3x} = \sqrt {2x - 4} \]
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Bình phương hai vế của phương trình ta có
x2 – 3x = 2x – 4
\( \Rightarrow \) x2 – 5x + 4 = 0
\( \Rightarrow \) x = 1 hoặc x = 4
Thay lần lượt hai nghiệm vào phương trình, ta thấy x = 4 thoả mãn
Vậy phương trình có nghiệm là x = 4
Câu 5:
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) ≤ 0 với \[\forall x \in \mathbb{R}\].
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trường hợp 1. m = 0. Khi đó f(x) = – 2x – 1 ≤ 0 \[ \Leftrightarrow x \ge - \frac{1}{2}\]
Vậy m = 0 không thỏa mãn f(x) ≤ 0 với \[\forall x \in \mathbb{R}\]
Trường hợp 2. m ≠ 0.
Khi đó: f(x) = mx2 – 2x – 1 < 0 với \[\forall x \in \mathbb{R}\]\[ \Leftrightarrow \left\{ \begin{array}{l}a = m < 0\\\Delta ' = 1 + m \le 0\end{array} \right. \Leftrightarrow m \le - 1\]
Vậy m ≤ – 1 thỏa mãn bài toán.
Câu 6:
Tích các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
\[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7 \Leftrightarrow {x^2} - 2x - 3 + 3\sqrt {{x^2} - 2x - 3} - 4 = 0\]
Đặt \[\sqrt {{x^2} - 2x - 3} = t(t \ge 0)\] ta có phương trình t2 + 3t – 4 =0\[ \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = - 4\end{array} \right.\]
Kết hợp với điều kiện của t ta có t = 1 thỏa mãn
Với t = 1 \[ \Rightarrow \sqrt {{x^2} - 2x - 3} = 1 \Leftrightarrow {x^2} - 2x - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 + \sqrt 5 \\x = 1 - \sqrt 5 \end{array} \right.\]
Thay lần lượt các nghiệm vào phương trình ta có \[x = 1 + \sqrt 5 ;x = 1 - \sqrt 5 \] đều thỏa mãn
Vậy tích các nghiệm của phương trình S = – 4.
Câu 7:
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] thuộc khoảng nào trong các khoảng sau
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Bình phương hai vế của phương trình đã cho ta có
x – 2 + x + 3 + 2\(\sqrt {(x - 2)(x + 3)} \) = 25
\( \Rightarrow \) \(\sqrt {{x^2} + x - 6} \) = 12 – x(1)
Bình phương hai vế của phương trình (1) ta có
x2 + x – 6 = (12 – x)2
\( \Rightarrow \) x2 + x – 6 = x2 – 24x + 144
\( \Rightarrow \) 25x – 150 = 0
\( \Rightarrow \) x = 6
Thay nghiệm trên vào phương trình ta thấy x = 6 thoả mãn
Vậy nghiệm của phương trình thuộc khoảng (3; 7)
Câu 8:
Với x thuộc tập hợp nào dưới đây thì f(x) = 2x2 – 7x – 15 không âm?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét f(x) = 2x2 – 7x – 15 có ∆ = 169 > 0, hai nghiệm phân biệt là x = 5; x = \( - \frac{3}{2}\) và a = 2 > 0
Ta có bảng xét dấu
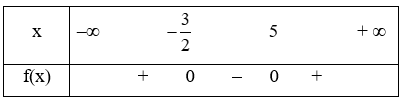
Từ bảng xét dấu ta có f(x) không âm khi x \( \in \) \[\left( { - \infty ; - \frac{3}{2}} \right] \cup \left[ {5; + \infty } \right)\].
Câu 9:
Biểu thức f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương khi và chỉ khi:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có (m2 + 2)x2 – 2(m – 2)x + 2 > 0 với mọi x \( \in \) ℝ\[ \Leftrightarrow \left\{ \begin{array}{l}a > 0\\{\Delta ^/} < 0\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 2 > 0\\ - {m^2} - 4m < 0\end{array} \right.\]
Ta có m2 + 2 > 0 với mọi m nên để (m2 + 2)x2 – 2(m – 2)x + 2 > 0 với mọi x \( \in \) ℝ thì – m2 – 4m < 0
Xét f(m) = – m2 – 4m có ∆ = 16 > 0, hai nghiệm phân biệt là m = 0; m = – 4 và a = – 1 < 0
Ta có bảng xét dấu
|
m |
– ∞ –4 0 + ∞ |
|
f(m) |
– 0 + 0 – |
Vậy để f(m) < 0 khi m < – 4 hoặc m > 0.
Câu 10:
Có bao nhiêu giá trị nguyên của m để bất phương trình x2 + 3mx2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có x2 + 3mx2 + 4mx + 4 ≥ 0
\( \Leftrightarrow \) (1 + 3m)x2 + 4mx + 4 ≥ 0
Với 1 + 3m = 0 thì m = \( - \frac{1}{3}\) thì bất phương trình trở thành \( - \frac{4}{3}\)x + 4 ≥ 0 ⇔ x ≤ 3. Vậy m = \( - \frac{1}{3}\) không thỏa mãn.
Với 1 + 3m ≠ 0 thì m ≠ \( - \frac{1}{3}\)
Để bất phương trình (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ thì
\( \Leftrightarrow \left\{ \begin{array}{l}1 + 3m > 0\\\Delta ' = 4{m^2} - 12m - 4 \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > - \frac{1}{3}\\4{m^2} - 12m - 4 \le 0\end{array} \right.\)
Xét f(m) = 4m2 – 12m – 4 có ∆ = 208 > 0, hai nghiệm phân biệt là x = \(\frac{{3 - \sqrt {13} }}{2}\) ; x = \(\frac{{3 + \sqrt {13} }}{2}\) và a = 4 > 0
Ta có bảng xét dấu
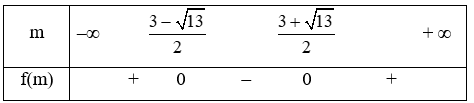
Từ bảng xét dấu ta có để f(m) ≤ 0 thì \(\frac{{3 - \sqrt {13} }}{2}\)≤ m ≤ \(\frac{{3 + \sqrt {13} }}{2}\)
Kết hợp với điều kiện của m để (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ thì \(\frac{{3 - \sqrt {13} }}{2}\)≤ m ≤ \(\frac{{3 + \sqrt {13} }}{2}\)
Vậy có 4 giá trị nguyên của m để bất phương trình (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ.
Câu 11:
Xác định m để bất phương trình x2 + 2(m – 2)x + 2m – 1 > 0 có nghiệm với mọi x \( \in \) ℝ.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Để bất phương trình x2 + 2(m – 2)x + 2m – 1 > 0 có nghiệm với mọi x \( \in \) ℝ thì \(\left\{ \begin{array}{l}a = 1 > 0\\\Delta ' < 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\{(m - 2)^2} - 2m + 1 < 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\{m^2} - 6m + 5 < 0\end{array} \right.\)
Xét f(m) = m2 – 6m + 5 có ∆ = 16 > 0 hai nghiệm phân biệt là m = 1 ; m = 5 và a = 1 > 0
Ta có bảng xét dấu
|
m |
–∞ 1 5 + ∞ |
|
f(m) |
+ 0 – 0 + |
Suy ra để f(m) < 0 thì 1 < m < 5.
Vậy với 1 < m < 5 thì bất phương trình x2 + 2(m – 2)x + 2m – 1 > 0 có nghiệm với mọi x \( \in \) ℝ.
Câu 12:
Số nghiệm của phương trình 4x2 – 12x + 5\(\sqrt {4{x^2} - 12x} \) = 0
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có 4x2 – 12x + 5\(\sqrt {4{x^2} - 12x} \) = 0
Đặt \(\sqrt {4{x^2} - 12x} \)= t (t ≥ 0)
Phương trình (1) trở thành t2 + 5t = 0 \( \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = - 5\end{array} \right.\)
Kết hợp với điều kiện t = 0 thoả mãn
Với t = 0 ta có \(\sqrt {4{x^2} - 12x} \)= 0
\( \Rightarrow \) 4x2 – 12x = 0
\( \Rightarrow \) x = 0 hoặc x = 3
Thay lần lượt các nghiệm trên vào phương trình, ta thấy x = 0 và x = 3 thoả mãn.
Vậy phương trình có hai nghiệm.
Câu 13:
Tích các nghiệm của phương trình x2 + 2\(\sqrt {{x^2} - 3x + 11} \) = 3x + 4 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có x2 + 2\(\sqrt {{x^2} - 3x + 11} \) = 3x + 4 \( \Leftrightarrow \) x2 – 3x + 11 + 2\(\sqrt {{x^2} - 3x + 11} \) – 15 = 0
Đặt \(\sqrt {{x^2} - 3x + 11} \) = t (t ≥ 0)
Phương trình trở thành t2 + 2t – 15 = 0 \( \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = - 5\end{array} \right.\)
Kết hợp với điều kiện t = 3 thoả mãn
Với t = 3 ta có \(\sqrt {{x^2} - 3x + 11} \) = 3
\( \Rightarrow \) x2 – 3x + 11 = 9
\( \Rightarrow \) x2 – 3x + 2 = 0
\( \Rightarrow \) x = 2 hoặc x = 1
Thay lần lượt các nghiệm trên vào phương trình, ta thấy x = 1 và x = 2 thoả mãn
Tích các nghiệm của phương trình là 1.2 = 2
Câu 14:
Tổng các nghiệm của phương trình \(\sqrt {x + 3} + \sqrt {6 - x} = 3 + \sqrt {(x + 3)(6 - x)} \) (*) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đặt \(\sqrt {x + 3} + \sqrt {6 - x} = t\) (t > 0) \( \Leftrightarrow \) x + 3 + 6 – x + \(2\sqrt {(x + 3)(6 - x)} \) = t2
Ta có \(\sqrt {(x + 3)(6 - x)} = \frac{{{t^2} - 9}}{2}\)
Phương trình (*) trở thành t = 3 + \(\frac{{{t^2} - 9}}{2}\)
\( \Leftrightarrow \) t2 – 2t – 3 = 0
\( \Leftrightarrow \) t = – 1 hặc t = 3
Kết hợp với điều kiện t = 3 thoả mãn
Với t = 3 ta có \(\sqrt {x + 3} + \sqrt {6 - x} = 3\)
\( \Rightarrow \) x + 3 + 6 – x + \(2\sqrt {(x + 3)(6 - x)} \) = 9
\( \Rightarrow \)\(\sqrt {(x + 3)(6 - x)} \)= 0
\( \Rightarrow \) – x2 + 3x + 18 = 0
\( \Rightarrow \)x = 6 hoặc x = – 3
Thay lần lượt các nghiệm trên vào phương trình, ta thấy x = 6 và x = – 3 thoả mãn
Tổng các nghiệm của phương trình là 6 + (– 3) = 3.
Câu 15:
Gọi x là nghiệm của phương trình
\(\sqrt {3x - 2} + \sqrt {x - 1} = 4x - 9 + 2\sqrt {3{x^2} - 5x + 2} \)
Tính giá trị của biểu thức A = x2 – 3x + 15
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
\(\sqrt {3x - 2} + \sqrt {x - 1} = 4x - 9 + 2\sqrt {3{x^2} - 5x + 2} \)(*)
Đặt \(\sqrt {3x - 2} + \sqrt {x - 1} = t(t > 0)\)
\( \Leftrightarrow \) 3x – 2 + x – 1 + 2\(\sqrt {3{x^2} - 5x + 2} \) = t2
\( \Leftrightarrow \) 4x – 3 + 2\(\sqrt {3{x^2} - 5x + 2} \) = t2
\( \Leftrightarrow \) 4x – 9 + 2\(\sqrt {3{x^2} - 5x + 2} \)= t2 – 6
Phương trình (*) trở thành t = t2 – 6
\( \Rightarrow \) t2 – t – 6 = 0
\( \Rightarrow \) t = 3 hoặc t = – 2.
Kết hợp với điều kiện t = 3 thoả mãn
Với t = 3 ta có \(\sqrt {3x - 2} + \sqrt {x - 1} = 3\)
\( \Rightarrow \) 4x – 3 + 2\(\sqrt {3{x^2} - 5x + 2} \)= 9
\( \Rightarrow \) \(\sqrt {3{x^2} - 5x + 2} \)= – 2x + 6
\( \Rightarrow \) 3x2 – 5x + 2 = (6 – 2x)2
\( \Rightarrow \) 3x2 – 5x + 2 = 4x2 – 24x + 36
\( \Rightarrow \) x2 – 19x + 34 = 0
\( \Rightarrow \) x1 = 17 hoặc x2 = 2
Thay lần lượt các nghiệm trên vào phương trình (*), ta thấy x2 = 2 thoả mãn
Giá trị của biểu thức A = 22 – 3.2 + 15 = 13.
