Trắc nghiệm Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án
Trắc nghiệm Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án
-
1057 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 2x + 1 là:
 Xem đáp án
Xem đáp án
Xét biếu thức f(x) = x2 + 2x + 1 có ∆ = 0 và nghiệm là x = – 1; a = 1 > 0.
Ta có bảng xét dấu như sau:

Đáp án đúng là D.
Câu 2:
Biểu thức nào sau đây là tam thức bậc hai
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét đáp án A có f(x) = x + 2 là nhị thức bậc nhất
Xét đáp án B có f(x) = 2x3 + 2x2 – 1 là biểu thức bậc ba
Xét đáp án C có f(x) = x2 – 3x là tam thức bậc hai
Xét đáp án D có f(x) = 2x – 1 là nhị thức bậc nhất
Câu 3:
Với x thuộc tập hợp nào dưới đây thì đa thức f(x) = x2 – 6x + 8 không dương?
 Xem đáp án
Xem đáp án
Để f(x) không dương thì x2 – 6x + 8 ≤ 0
Xét biểu thức f(x) = x2 – 6x + 8 có ∆ = 4 > 0, hai nghiệm phân biệt là x = 2; x = 4 và a = 1 > 0.
Ta có bảng xét dấu sau

Từ bảng xét dấu f(x) ta thấy để f(x) ≤ 0 thì x [2; 4]
Câu 4:
Các giá trị m làm cho biểu thức f(x) = x2 + 4x + m + 3 luôn dương là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: f(x) = x2 + 4x + m + 3 luôn luôn dương \[ \Leftrightarrow \] x2 + 4x + m + 3 > 0 với mọi x \[ \in \]ℝ \[ \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\\Delta ' = {2^2} - (m + 3) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\m > 1\end{array} \right.\].
Vậy đáp án đúng là C.
Câu 5:
Tam thức nào sau đây nhận giá trị âm với mọi x < 1
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét đáp án A: f(x) = x2 – 5x + 6
Xét biểu thức f(x) = x2 – 5x + 6 có ∆ = 1 > 0, hai nghiệm phân biệt là x = 2 ; x = 3 và a = 1 > 0
Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức f(x) = x2 – 5x + 6 nhận giá trị âm khi 2 < x < 3.
Vậy đáp án A sai.
Xét đáp án B: f(x) = x2 – 16
Xét biểu thức f(x) = x2 – 16 có ∆’ = 16 > 0, hai nghiệm phân biệt là x = 4 ; x = – 4 ; và a = 1 > 0. Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức f(x) = x2 – 16 nhận giá trị âm khi – 4 < x < 4
Vậy đáp án B sai.
Xét đáp án C: f(x) = x2 + 2x + 3
Xét biểu thức f(x) = x2 + 2x + 3 = 0 có ∆ < 0 \[ \Leftrightarrow \]Phương trình vô nghiệm và a = 1 > 0
Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức y = x2 – 2x + 3 nhận giá trị dương với mọi x \[ \in \]ℝ
Vậy đáp án C sai.
Xét đáp án D: y = – x2 + 5x – 4.
Xét biểu thức f(x) = – x2 + 5x – 4 = 0 có ∆ = 9 > 0, hai nhiệm phân biệt là x = 1, x = 4 và a = – 1 < 0
Ta có bảng xét dấu

Dựa vào bảng xét dấu ta có tam thức y = – x2 + 5x – 6 nhận giá trị âm khi \[x \in ( - \infty ;1) \cup (4; + \infty )\].
Vậy đáp án D đúng.
Câu 6:
Cho hàm số f(x) = mx2 – 2mx + m – 1. Giá trị của m để f(x) < 0 \(\forall x \in \mathbb{R}\).
 Xem đáp án
Xem đáp án
Trường hợp 1, m = 0. Khi đó: f(x) = – 1 < 0\(\forall x \in \mathbb{R}\). Vậy m = 0 thoả mãn bài toán.
Trường hợp 2, m ≠ 0. Khi đó:
f(x) = mx2 – 2mx + m – 1 < 0 \(\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a = m < 0\\\Delta ' = {m^2} - m\left( {m - 1} \right) < 0\end{array} \right.\).\( \Leftrightarrow \left\{ \begin{array}{l}a = m < 0\\m < 0\end{array} \right. \Leftrightarrow m < 0\)
Vậy m ≤ 0 thỏa mãn bài toán.
Câu 7:
Tìm tất cả các giá trị thực của tham số m để f(x) = (m – 3)x2 + (m + 2)x – 4 nhận giá trị không dương với mọi giá trị của x.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có f(x) nhận giá trị không dương với mọi x \( \Leftrightarrow f\left( x \right) \le 0\,\,\forall x \in \mathbb{R}\).
Xét m = 3 ta có f(x) = 5x – 4 với f(x) ≤ 0 thì \(x \le \frac{4}{5}\) nên m = 3 không thỏa mãn.
Xét m ≠ 3 ta có \(f\left( x \right) \le 0\,\,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a = m - 3 < 0\\\Delta = {m^2} + 20m - 44 \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < 3\\{m^2} + 20m - 44 \le 0\end{array} \right.\)
Xét m2 + 20m – 44 = 0\( \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 22\end{array} \right.\)
Ta có bảng xét dấu

Để \(f\left( x \right) \le 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}m < 3\\ - 22 \le m \le 2\end{array} \right. \Leftrightarrow - 22 \le m \le 2\)
Vậy đáp án đúng là B.
Câu 8:
Tìm tất cả các giá trị của m để tam thức f(x) = mx2 – x + m luôn dương với \(\forall x \in \mathbb{R}\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
+) Với m = 0 thì f(x) = – x, f(x) > 0 ⇔ – x > 0 ⇔ x < 0. Do đó m = 0 không thỏa mãn.
Ta có để f(x) = mx2 – x + m > 0, \(\forall x \in \mathbb{R}\) \( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\Delta = {\left( { - 1} \right)^2} - 4.m.m < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\1 - 4{m^2} < 0\end{array} \right.\)
Xét biểu thức g(m) = 1 – 4m2 có ∆ = 16 > 0, hai nghiệm phân biệt là m = \(\frac{1}{2}\), m = \( - \frac{1}{2}\) và a = – 4 < 0
Ta có bảng xét dấu
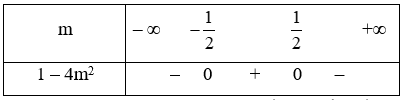
Dựa vào bảng xét dấu ta có 1 – 4m2 < 0 \( \Leftrightarrow m \in \left( { - \infty ; - \frac{1}{2}} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\);
Vậy để f(x) = mx2 – x + m nhận giá trị dươngn , \(\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\m \in \left( { - \infty ; - \frac{1}{2}} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\end{array} \right. \Leftrightarrow m > \frac{1}{2}\)
Câu 9:
Tam thức y = – x2 – 3x – 4 nhận giá trị âm khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét tam thức y = – x2 – 3x – 4 có ∆ = – 7, và a = – 1 < 0
Ta có bảng xét dấu

Từ bảng xét dấu ta có tam thức y = – x2 – 3x – 4 nhận giá trị âm với mọi x \( \in \) ℝ.
Câu 10:
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x \( \in \) ℝ.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trường hợp 1, m = 0 ta có f(x) < 0 \( \Leftrightarrow \) – 2x – 1 < 0 \( \Leftrightarrow x > - \frac{1}{2}\)
Do đó m = 0 không thỏa yêu cầu bài toán.
Trường hợp 2, m ≠ 0
Ta có để f(x) < 0 với mọi x \( \in \) ℝ \[ \Leftrightarrow \left\{ \begin{array}{l}m < 0\\\Delta ' < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\1 + m < 0\end{array} \right. \Leftrightarrow m < - 1\].
Câu 11:
Xác định m để biểu thức f(x) = (m + 2)x2 – 3mx + 1 là tam thức bậc hai
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Để biểu thức f(x) = (m + 2)x2 – 3mx + 1 là tam thức bậc hai thì m + 2 ≠ 0 \( \Leftrightarrow \) m ≠ – 2.
Câu 12:
Biểu thức f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương \( \Leftrightarrow \)(m2 + 2)x2 – 2(m – 2)x + 2 > 0 với mọi x \( \in \) ℝ \[ \Leftrightarrow \left\{ \begin{array}{l}a > 0\\{\Delta ^/} < 0\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 2 > 0\\ - {m^2} - 4m < 0\end{array} \right.\]
Vì m2 + 2 > 0 với mọi m nên để (m2 + 2)x2 – 2(m – 2)x + 2 > 0 thì – m2 – 4m < 0
Xét f(m) = – m2 – 4m có ∆ = 16 > 0, hai nghiệm phân biệt là m = 0; m = – 4 và a = – 1 < 0. Ta có bảng xét dấu:

Vậy để – m2 – 4m < 0 thì m < – 4 hoặc m > 0.
Câu 13:
Các giá trị m để tam thức f(x) = x2 – (m + 2)x + 8m + 1 đổi dấu 2 lần là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: f(x) = x2 – (m + 2)x + 8m + 1 đổi dấu \(2\) lần khi phương trình x2 – (m + 2)x + 8m + 1 = 0 có 2 nghiệm phân biệt
Vậy ∆ = (– (m + 2))2 – 4.1.(8m + 1) > 0 \( \Leftrightarrow \) m2 – 28m > 0
Xét f(m) = m2 – 28m có ∆’ = 196 > 0, hai nghiệm phân biệt là m = 0; m = 28 và a = 1 > 0. Ta có bảng xét dấu

Từ bảng xét dấu để m2 – 28m > 0 thì m < 0 hoặc m > 28.
Vậy tam thức f(x) đổi dấu 2 lần khi m < 0 hoặc m > 28.
Câu 14:
Cho tam thức f(x) = x2 + 2mx + 3m – 2. Tìm m để f(x) ≥ 0 với mọi x \( \in \) ℝ.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Để f(x) ≥ 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\\Delta ' \le 0\end{array} \right.\)
Ta có ∆’ = m2 – 3m + 2 ≤ 0
Xét f(m) = m2 – 3m + 2 có ∆ = 1 > 0, hai nghiệm phân biệt là m = 1; m = 2 và a = 1 > 0. Ta có bản xét dấu

Từ bảng xét dấu ta có để m2 – 3m + 2 ≤ 0 thì 1 ≤ m ≤ 2.
Vậy với 1 ≤ m ≤ 2 thì f(x) ≥ 0 với mọi x \( \in \) ℝ.
Câu 15:
Cho tam thức bậc hai f(x) = ax2 + bx + c có đồ thị như hình vẽ dưới đây
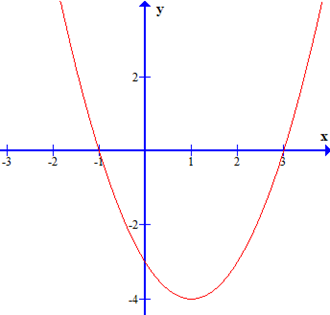
Bảng biến thiên của tam thức bậc hai là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Từ đồ thị ta có:
Đồ thị hàm số cắt trục hoành tại 2 điểm có hoành độ x = – 1 và x = 3 nên f(x) có 2 nghiệm phân biệt là x = –1; x = 3 ta loại đáp án C và D.
f(x) nhận giá trị dương trên các khoảng (– ∞; –1) và (3; + ∞); f(x) nhận giá trị âm trên khoảng (–1; 3) ta loại đáp án B.
