30 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án (Đề 2)

Câu 1:

(u_{n})

với

u_{n} = \frac{1}{2} n + 1

. Khẳng định nào sau đây là đúng?

A. Hiệu

u_{n + 1} - u_{n} = \frac{1}{2}

B. Tổng của 5 số hạng đầu tiên là $S_{5} = 12$

C. Dãy số này không phải là cấp số cộng.

D. Số hạng thứ

n + 1

là

u_{n + 1} = \frac{1}{2} n

Xem đáp án

Chọn A

Câu 2:

Có bao nhiêu số nguyên m để phương trình $5 \sin x - 12 \cos x = m$ có nghiệm?

A. 27.

B. Vô số.

C. 26.

D. 13.

Xem đáp án

Chọn A

Câu 3:

Mệnh đề nào sau đây sai?

A.

\sin x = 0 \Leftrightarrow x = k 2 π

B. $\sin x = 1 \Leftrightarrow x = \frac{π}{2} + k 2 π$

C. $\sin x = - 1 \Leftrightarrow x = - \frac{π}{2} + k 2 π$

D. $\sin x = 0 \Leftrightarrow x = k π$

Xem đáp án

Chọn A

Câu 4:

Trong mặt phẳng Oxy, cho phép biến hình f xác định như sau: Với mỗi $M (x; y)$ ta có $M^{'} = f (M)$ sao cho $M^{'} (x^{'}; y^{'})$ thỏa mãn $x^{'} = x + 2, y^{'} = y - 3$ . Khẳng định đúng là

A. f là phép tịnh tiến theo vectơ $\vec{v} = (2; 3)$

B. f là phép tịnh tiến theo vectơ $\vec{v} = (- 2; 3)$

C. f là phép tịnh tiến theo vectơ $\vec{v} = (- 2; - 3)$

D. f là phép tịnh tiến theo vectơ

\vec{v} = (2; - 3)

Xem đáp án

Chọn D

Câu 5:

Tập xác định của hàm số $y = \tan 3 x$ là

A. $D = ℝ \ \{k \frac{2 π}{3}, k \in ℤ\}$

B. $D = ℝ \ \{\frac{π}{6} + k \frac{π}{3}, k \in ℤ\}$

C. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$

D. $D = ℝ \ \{π + k π, k \in ℤ\}$

Xem đáp án

Chọn B

Câu 6:

Chọn khẳng định sai trong các khẳng định sau

A. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.

B. Nếu ba điểm phân biệt M, N, P cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.

C. Hai mặt phẳng có một điểm chung thì chúng còn có thể có vô số điểm chung khác nữa.

D. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.

Xem đáp án

Chọn D

Câu 7:

Trong khai triển ${(a + 2)}^{n + 6} (n \in ℕ)$ có tất cả 17 số hạng. Vậy n bằng

A. 17.

B. 12.

C. 10.

D. 11.

Xem đáp án

Chọn C

Câu 8:

Một hộp đựng 10 thẻ đánh số từ 1 đến 10. Chọn ngẫu nhiên 3 thẻ. Gọi A là biến cố để tổng số của 3 thẻ được chọn không vượt quá 8. Số phần tử của biến cố A là

A. 5.

B. 2.

C. 3.

D. 4.

Xem đáp án

Chọn D

Câu 9:

Gọi X là tập nghiệm phương trình $\cos (\frac{x}{2} + 15 °) = \sin x$ . Mệnh đề nào sau đây là đúng?

A. $220 ° \in X$

B. $240 ° \in X$

C. $290 ° \in X$

D. $20 ° \in X$

Xem đáp án

Chọn C

Câu 10:

Cho tam giác đều ABC. Góc quay của phép quay tâm A biến B thành C là

A. $φ = 30 °$

B. $φ = 90 °$

C. $φ = - 30 °$

D. $φ = 60 °$ hoặc $φ = - 60 °$

Xem đáp án

Chọn D

Câu 11:

Cho hình chóp S.ABCD có đáy là hình thang ABCD (AD // BC). Gọi M là trung điểm CD. Giao tuyến của hai mặt phẳng (MSB) và (SAC) là

A. SP với P là giao điểm AB và CD.

B. SJ với J là giao điểm AM và BD

C. SO với O là giao điểm AC và BD.

D. SI với I là giao điểm AC và BM.

Xem đáp án

Chọn D

Câu 12:

Với $k \in ℤ$ , kết luận nào sau đây về hàm số $y = \tan 2 x$ là sai?

A. Hàm số

y = \tan 2 x

tuần hoàn với chu kỳ

T = \frac{π}{2}

.

B. Hàm số $y = \tan 2 x$ luôn đồng biến trên mỗi khoảng . $(- \frac{π}{2} + \frac{k π}{2}; \frac{π}{2} + \frac{k π}{2})$

C. Hàm số $y = \tan 2 x$ nhận đường thẳng $x = \frac{π}{4} + \frac{k π}{2}$ là một đường tiệm cận.

D. Hàm số

y = \tan 2 x

là hàm số lẻ.

Xem đáp án

Chọn B

Câu 13:

Một tổ gồm 7 nam và 6 nữ. Hỏi có bao nhiêu cách chọn 4 em đi trực sao cho có ít nhất 2 nữ?

A. $(C_{7}^{2} . C_{6}^{2}) + (C_{7}^{1} . C_{6}^{3}) + C_{6}^{4}$

B. $C_{11}^{2} . C_{12}^{2}$

C. $C_{7}^{2} . C_{6}^{2} + C_{7}^{3} . C_{6}^{1} + C_{7}^{4}$

D. $(C_{7}^{2} + C_{6}^{5}) + (C_{7}^{1} + C_{6}^{3}) + C_{6}^{4}$

Xem đáp án

Chọn A

Câu 14:

Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

A. $a^{2} - c^{2} = 2 a b - 2 b c$

B. $a^{2} + c^{2} = 2 a b - 2 b c$

C. $a^{2} - c^{2} = a b - b c$

D. $a^{2} + c^{2} = 2 a b + 2 b c$

Xem đáp án

Chọn A

Câu 15:

Số giá trị nguyên của tham số m thuộc đoạn $[- 2018; 2021]$ để phương trình $(m + 1) \sin^{2} x - \sin 2 x + \cos 2 x = 0$ có nghiệm là

A. 4037.

B. 2020.

C. 2019.

D. 4036.

Xem đáp án

Chọn B

Câu 16:

Cho tập A gồm n điểm phân biệt trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng. Giá trị của n để số tam giác có 3 đỉnh lấy từ 3 điểm thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A

A. n=12

B. n=8

C. n=15

D. n=6

Xem đáp án

Chọn B

Câu 17:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình $2 x + y - 3 = 0$ . Phép vị tự tâm O tỉ số k=2 biến d thành đường thẳng nào trong các đường thẳng sau?

A. $4 x + 2 y - 5 = 0$

B. $2 x + y + 3 = 0$

C. $2 x + y - 6 = 0$

D. $4 x - 2 y - 3 = 0$

Xem đáp án

Chọn C

Câu 18:

Giá trị nhỏ nhất của hàm số $y = \frac{\sin x + 1}{\cos x + 2}$ là

A. $\frac{- \sqrt{2}}{2}$

B. $\frac{- \sqrt{2}}{2}$

C. 0

D. $\frac{1}{2}$

Xem đáp án

Chọn C

Câu 19:

Cho cấp số nhân $(u_{n})$ với $u_{1} = 3; q = \frac{- 1}{2}$ . Số 222 là số hạng thứ mấy của $(u_{n})$ ?

A. Số hạng thứ 9.

B. Không thuộc cấp số nhân đã cho .

C. Số hạng thứ 11.

D. Số hạng thứ 12.

Xem đáp án

Chọn B

Câu 20:

Một người viết ngẫu nhiên một số có bốn chữ số. Xác suất để các chữ số của số được viết ra có thứ tự tăng dần hoặc giảm dần (nghĩa là nếu số được viết dưới dạng $\bar{a b c d}$ thì $a < b < c < d$ hoặc $a > b > c > d$ ) là

A. $\frac{7}{375}$

B. $\frac{7}{250}$

C. $\frac{14}{375}$

D. $\frac{7}{125}$

Xem đáp án

Chọn C

Câu 21:

a) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = \sin x - \cos x - \sqrt{2}$ .

Xem đáp án

a) Ta có $y = \sin x - \cos x - \sqrt{2} = \sqrt{2} \sin (x - \frac{π}{4}) - \sqrt{2}$

Mà $- 1 \leq \sin (x - \frac{π}{4}) \leq 1$ nên $- 2 \sqrt{2} \leq \sqrt{2} \sin (x - \frac{π}{4}) - \sqrt{2} \leq 0 \Leftrightarrow - 2 \sqrt{2} \leq y \leq 0$

Vậy $\max y = 0$ khi và chỉ khi $\sin (x - \frac{π}{4}) = 1 \Leftrightarrow x = \frac{3 π}{4} + k 2 π (k \in ℤ)$ .

\min y = - 2 \sqrt{2}

khi và chỉ khi .

\sin (x - \frac{π}{4}) = - 1 \Leftrightarrow x = - \frac{π}{4} + k 2 π (k \in ℤ)

Câu 22:

b) Giải phương trình $2 \sin^{2} x - 5 \sin x \cos x - \cos^{2} x = 2$ .

Xem đáp án

b) Với $\cos x = 0 \Rightarrow \sin^{2} x = 1$

Thay vào phương trình ta được 2=2 (luôn đúng)

$\Rightarrow \cos x = 0 \Leftrightarrow x = \frac{π}{2} + k π$ là nghiệm của phương trình đã cho.

Với $\cos x \neq 0$ chia cả hai vế của phương trình cho $\cos^{2} x$ , ta được

$2 \tan^{2} x - 5 \tan x - 1 = 2. \frac{1}{\cos^{2} x} \Leftrightarrow 2 \tan^{2} x - 5 \tan x - 1 = 2 (1 + \tan^{2} x)$

$\Leftrightarrow \tan x = - \frac{3}{5} \Leftrightarrow x = \arctan x (- \frac{3}{5}) + k π (k \in ℤ)$

Vậy phương trình đã cho có 2 họ nghiệm

[\begin{array}{l} x = \frac{π}{2} + k π \\ x = \arctan x (- \frac{3}{5}) + k π \end{array} (k \in ℤ)

Câu 23:

c) Tìm tất cả các giá trị thực của tham số m để phương trình $2 \cos^{2} 3 x + (3 - 2 m) \cos 3 x + m - 2 = 0$ có đúng 3 nghiệm thuộc khoảng $(- \frac{π}{6}; \frac{π}{3})$ .

Xem đáp án

c) Đặt $t = \cos 3 x (- 1 \leq t \leq 1)$

Phương trình trở thành $2 t^{2} + (3 - 2 m) t + m - 2 = 0$

Ta có $Δ = {(2 m - 5)}^{2} \geq 0$ . Suy ra phương trình có hai nghiệm $[\begin{array}{l} t_{1} = \frac{1}{2} \\ t_{2} = m - 2 \end{array}$

Ta thấy ứng với một nghiệm $t_{1} = \frac{1}{2}$ thì cho ta hai nghiệm x thuộc khoảng $(- \frac{π}{6}; \frac{π}{3})$

Để phương trình đã cho có đúng 3 nghiệm thuộc khoảng $(- \frac{π}{6}; \frac{π}{3})$ thì phương trình $\cos 3 x = m - 2$ có đúng 1 nghiệm thuộc khoảng $(- \frac{π}{6}; \frac{π}{3})$

$\Leftrightarrow - 1 < m - 2 \leq 0 \Leftrightarrow 1 < m \leq 2$

Câu 24:

a) Trong một hộp chứa sáu quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen được đánh số 7, 8, 9. Có bao nhiêu cách chọn một trong các quả cầu ấy?

Xem đáp án

a) Vì các quả cầu trắng hoặc đen đều được đánh số phân biệt nên mỗi lần lấy ra một quả cầu bất kì là một lần chọn.

* Nếu chọn một quả trắng có 6 cách.

* Nếu chọn một quả đen có 3 cách.

Theo quy tắc cộng, ta có 6+3=9 cách chọn.

Câu 25:

b) Gieo một con súc sắc cân đối và đồng chất. Giả sử con súc sắc xuất hiện mặt b chấm. Tính xác suất sao cho phương trình $x^{2} - b x + b - 1 = 0$ (x là ẩn số) có nghiệm lớn hơn 3.

Xem đáp án

b) Ta có $n (Ω) = 6$

Xét phương trình $x^{2} - b x + b - 1 = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = b - 1 \end{array}$

Phương trình có nghiệm lớn hơn 3 $\Leftrightarrow b - 1 > 3 \Leftrightarrow b > 4$

Mặt khác, con súc sắc có 6 mặt với số chấm trên mỗi mặt là b thỏa mãn $1 \leq b \leq 6, b \in ℕ$

Do đó $b \in \{5; 6\}$

Gọi A là biến cố: “Phương trình có nghiệm lớn hơn 3” hay A là biến cố: “ $b = 5$ hoặc $b = 6$ ” $\Rightarrow n (A) = 2$

Vậy xác suất là

P (A) = \frac{2}{6} = \frac{1}{3}

Câu 26:

c) Từ một nhóm học sinh lớp 10A gồm 5 bạn học giỏi môn Toán, 4 bạn học giỏi môn Lý, 3 bạn học giỏi môn Hóa, 2 bạn học giỏi môn Văn (mỗi học sinh chỉ giỏi đúng một môn). Đoàn trường chọn ngẫu nhiên 4 học sinh để tham gia thi “hành trình tri thức”. Tính xác suất để chọn được 4 học sinh sao cho có ít nhất 1 bạn học giỏi Toán và ít nhất 1 bạn học giỏi Văn.

Xem đáp án

c) Không gian mẫu là số cách chọn ngẫu nhiên 4 bạn học sinh trong 14 bạn học sinh.

Suy ra số phần tử của không gian mẫu là $|Ω| = C_{14}^{4} = 1001$

Gọi A là biến cố: “Chọn được 4 học sinh sao cho có ít nhất 1 bạn học giỏi Toán và ít nhất 1 bạn học giỏi Văn”.

Các trường hợp thuận lợi cho biến cố A là

Trường hợp 1: 1 học sinh giỏi Toán; 1 học sinh giỏi Văn; 2 học sinh môn khác.

Có $C_{5}^{1} . C_{2}^{1} . C_{7}^{2}$ cách chọn.

Trường hợp 2: 1 học sinh giỏi Toán; 2 học sinh giỏi Văn; 1 học sinh môn khác.

Có $C_{5}^{1} C_{2}^{2} C_{7}^{1}$ cách chọn.

Trường hợp 3: 2 học sinh giỏi Toán; 1 học sinh giỏi Văn; 1 học sinh môn khác.

Có $C_{5}^{2} C_{2}^{1} C_{7}^{1}$ cách chọn.

Trường hợp 4: 2 học sinh giỏi Toán; 2 học sinh giỏi Văn. Có $C_{5}^{2} C_{2}^{2}$ cách chọn.

Trường hợp 5: 3 học sinh giỏi Toán; 1 học sinh giỏi Văn. Có $C_{5}^{3} C_{2}^{1}$ cách chọn.

Vậy $|Ω_{A}| = 415$

Vậy xác suất cần tính

P (A) = \frac{|Ω_{A}|}{|Ω|} = \frac{415}{1001}

Câu 27:

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M và N lần lượt là trung điểm của AB và SC.

a) Xác định giao điểm I, K của đường thẳng AN, MN với (SBD).

Xem đáp án

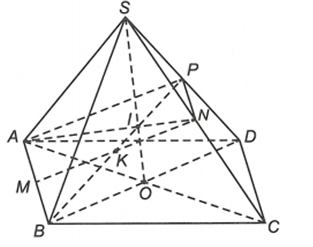
a) Gọi O là giao của AC và BD.

Trong (SAC), kẻ SO, AN. $S O \cap A N = \{I\}$

Kẻ

P N / ​ / A B (P \in S D) . B P \cap M N = \{K\}

Câu 28:

b) Chứng minh ba điểm B, I, K thẳng hàng.

Xem đáp án

b) Theo cách dựng ở câu a) ta có B, P, K thẳng hàng.

Vậy cần chứng minh B, I, P thẳng hàng.

ABCD là hình bình hành nên O là trung điểm của AC, N là trung điểm của SC.

Suy ra I là trọng tâm ∆SAC suy ra $\frac{I N}{I A} = \frac{1}{2} = \frac{I O}{S I}$ .

Giả sử $B P \cap S O = \{I^{'}\}$ ; PN // AB // CD suy ra P là trung điểm của SD

$\Rightarrow I^{'}$ là trọng tâm ∆SBD $\Rightarrow \frac{I^{'} O}{I^{'} S} = \frac{I^{'} P}{I^{'} B} = \frac{1}{2}$

Mà $\frac{I O}{I S} = \frac{I^{'} O}{I^{'} S} = \frac{1}{2}$ nên $I \equiv I^{'}$ hay B, I, P thẳng hàng.

Vậy ta có B, I, K thẳng hàng.

Câu 29:

c) Xác định thiết diện của hình chóp S.ABCD khi cắt bởi (ABN).

Xem đáp án

c) Thiết diện cần tìm là ABNP

Câu 30:

d) Tính các tỷ số $\frac{I A}{I N}, \frac{K M}{K N}, \frac{I B}{I K}$

Xem đáp án

d) $\frac{I A}{I N} = 2$ do I là trọng tâm ∆SAC.

Các tứ giác AMNP, BMNP là hình bình hành (do $P N / / A B; P N = A M = \frac{1}{2} A B$ )

nên $Δ N P K = Δ M B K \Rightarrow K N = K M \Rightarrow \frac{K M}{K N} = 1$ .

Ta có $K P = K B = \frac{1}{2} B P; I P = \frac{1}{3} P B; I B = \frac{2}{3} P B$

$I K = B P - K B - I P = B P - \frac{B P}{2} - \frac{B P}{3} = \frac{B P}{6} \Rightarrow \frac{I B}{I K} = \frac{\frac{2}{3} B P}{\frac{1}{6} B P} = 4$

Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án

Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương