30 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án (Đề 1)

Câu 1:

Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển ${(1 + 2 x)}^{10}$ là

A. $1, 45 x, 120 x^{2}$

B. $1, 4 x, 4 x^{2}$

C. $1, 20 x, 180 x^{2}$

D. $10, 45 x, 120 x^{2}$

Xem đáp án

Chọn C

Câu 2:

Cho cấp số cộng $(u_{n})$ có $u_{2} = 3$ và $u_{4} = 7$ . Giá trị của $u_{15}$ bằng

A. 31.

B. 35.

C. 29.

D. 27.

Xem đáp án

Chọn C

Câu 3:

Cho phép tịnh tiến $T_{\vec{u}}$ biến điểm M thành $M_{1}$ và phép tịnh tiến $T_{\vec{v}}$ biến $M_{1}$ thành $M_{2}$ . Chọn khẳng định đúng trong các khẳng định sau

A. Một phép đối xứng trục biến M thành $M_{2}$ .

B. Không thể khẳng định được có hay không một phép dời hình biến M thành $M_{2}$ .

C. Phép tịnh tiến $T_{\vec{u} + \vec{v}}$ biến M thành $M_{2}$ .

D. Phép tịnh tiến

T_{\vec{u} + \vec{v}}

biến

M_{1}

thành

M_{2}

.

Xem đáp án

Chọn C

Câu 4:

Điều kiện xác định của hàm số $y = \tan x + \cot x$ là

A. $x \neq \frac{k π}{2}, k \in ℤ$

B. $x \neq \frac{π}{2} + k π, k \in ℤ$

C. $x \in ℝ$

D. $x \neq k π, k \in ℤ$

Xem đáp án

Chọn A

Câu 5:

Phương trình $\sin x + \sqrt{3} \cos x = 1$ có tập nghiệm là

A.

\{\frac{7 π}{6} + k 2 π; \frac{π}{2} + k 2 π\}

, với

k \in ℤ

.

B. $\{- \frac{π}{6} + k π; - \frac{π}{2} + k π\}$ , với $k \in ℤ$

C.

\{- \frac{π}{6} + k 2 π; \frac{π}{2} + k 2 π\}

, với

k \in ℤ

.

D.

\{- \frac{π}{6} + k 2 π; - \frac{π}{2} + k 2 π\}

, với

k \in ℤ

Xem đáp án

Chọn C

Câu 6:

Cho hai đường thẳng phân biệt a và b cùng thuộc mp $(α)$ . Có bao nhiêu vị trí tương đối giữa a và b?

A. 3.

B. 4.

C. 1.

D. 2.

Xem đáp án

Chọn A

Câu 7:

Tất cả các giá trị thực của tham số m để phương trình $\sin x = m$ có nghiệm là.

A. $- 1 \leq m \leq 1$

B. $m \leq - 1$

C. $m \leq 1$

D. $m \geq - 1$

Xem đáp án

Chọn A

Câu 8:

Một hộp chứa 11 quả cầu gồm 5 quả cầu màu xanh và 6 quả cầu màu đỏ. Chọn ngẫu nhiên lần lượt hai quả cầu từ hộp đó. Xác suất để hai quả cầu được chọn ra cùng màu bằng

A. $\frac{25}{33}$

B. $\frac{25}{66}$

C. $\frac{5}{22}$

D. $\frac{5}{11}$

Xem đáp án

Chọn D

Câu 9:

Cho hình chóp S.ABCD. Gọi I là trung điểm của SD, J là điểm trên SC và không trùng trung điểm SC. Giao tuyến của hai mặt phẳng (ABCD) và (AIJ) là

A. AG với G là giao điểm IJ và AD.

B. AF với F là giao điểm IJ và CD.

C. AK với K là giao điểm IJ và BC.

D. AH với H là giao điểm IJ và AB.

Xem đáp án

Chọn B

Câu 10:

Nghiệm của phương trình

\sin^{4} x - \cos^{4} x = 0

là

A. $x = \frac{π}{2} + \frac{k π}{2} (k \in ℤ)$

B. $x = \frac{π}{3} + \frac{k π}{2} (k \in ℤ)$

C. $x = \frac{π}{6} + \frac{k π}{2} (k \in ℤ)$

D. $x = \frac{π}{4} + \frac{k π}{2} (k \in ℤ)$

Xem đáp án

Chọn D

Câu 11:

Có 10 quyển sách Toán giống nhau, 11 quyển sách Lý giống nhau và 9 quyển sách Hóa giống nhau. Có bao nhiêu cách trao giải thưởng cho 15 học sinh có kết quả thi học kì cao nhất của lớp, biết mỗi phần thưởng là hai quyển sách khác loại?

A. $C_{15}^{3} C_{9}^{4}$ cách

B. $C_{30}^{2}$ cách

C. $C_{15}^{7} C_{9}^{3}$ cách

D. $C_{15}^{6} C_{9}^{4}$ cách

Xem đáp án

Chọn D

Câu 12:

Hàm số $y = \sin 2 x$ nghịch biến trên các khoảng nào sau đây $(k \in ℤ)$ ?

A. $(\frac{π}{2} + k 2 π; \frac{3 π}{2} + k 2 π)$

B. $(- \frac{π}{4} + k π; \frac{π}{4} + k π)$

C. $(k 2 π; π + k 2 π)$

D. $(\frac{π}{4} + k π; \frac{3 π}{4} + k π)$

Xem đáp án

Đáp án D

Câu 13:

Cho hình chữ nhật tâm O. Hỏi có bao nhiêu phép quay tâm O một góc $α$ với $0 \leq α < 2 π$ , biến hình chữ nhật trên thành chính nó?

A. 2.

B. 3.

C. 4.

D. 0.

Xem đáp án

Chọn A

Câu 14:

Cho cấp số cộng $(u_{n})$ có $u_{4} = - 12, u_{14} = 18$ . Tổng 16 số hạng đầu tiên của cấp số cộng là

A. $S_{16} = - 25$

B. $S_{16} = 24$

C. $S_{16} = - 24$

D. $S_{16} = 26$

Xem đáp án

Chọn B

Câu 15:

Giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 2 \cos^{2} x - 2 \sqrt{3} sincos x + 1$ là

A. $\min y = - 1 + \sqrt{3}; \max y = 3 + \sqrt{3}$

B. $\min y = 0; \max y = 4$

C. $\min y = 1 - \sqrt{3}; \max y = 3 + \sqrt{3}$

D. $\min y = - 4; \max y = 0$

Xem đáp án

Chọn B

Câu 16:

Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn 100°?

A. $2018. C_{895}^{3}$

B. $2018. C_{896}^{2}$

C. $2018. C_{897}^{3}$

D. $C_{1009}^{3}$

Xem đáp án

Chọn B

Câu 17:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình $x + y - 2 = 0$ . Phép vị tự tâm O tỉ số k=-2 biến d thành đường thẳng nào trong các đường thẳng sau?

A. x+y+4=0

B. x+y-4=0

C. 2x+2y=0

D. 2x+2y-4=0

Xem đáp án

Chọn A

Câu 18:

Cho cấp số nhân $(u_{n})$ với $u_{1} = - 1; q = \frac{- 1}{10}$ . Số $\frac{1}{10^{103}}$ số hạng thứ mấy của $(u_{n})$ ?

A. Số hạng thứ 105.

B. Không là số hạng của cấp số đã cho.

C. Số hạng thứ 103.

D. số hạng thứ 104.

Xem đáp án

Chọn D

Câu 19:

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = \frac{\sin x + \cos x}{2 \sin x - \cos x + 3}$ lần lượt là

A.

m = 1; M = 2

B. $m = - 1; M = \frac{1}{2}$

C.

m = - 1; M = 2

D.

m = - \frac{1}{2}; M = 1

Xem đáp án

Chọn C

Câu 20:

Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau và chia hết cho 15?

A. 120.

B. 222.

C. 240.

D. 200.

Xem đáp án

Chọn B

Câu 21:

a) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = \cos x + \cos (x - \frac{π}{3})$ .

Xem đáp án

a) Ta có

$y = \cos x + \cos (x - \frac{π}{3}) = 2 \cos (\frac{x + x - \frac{π}{3}}{2}) \cos (\frac{x - x + \frac{π}{3}}{2}) = \sqrt{3} \cos (x - \frac{π}{6})$

Vì $- 1 \leq \cos (x - \frac{π}{6}) \leq 1, \forall x \in ℝ$ nên $- \sqrt{3} \leq \sqrt{3} \cos (x - \frac{π}{6}) \leq \sqrt{3}, \forall x \in ℝ$ .

Vậy $\min y = - \sqrt{3}$ khi $\cos (x - \frac{π}{6}) = - 1 \Leftrightarrow x = \frac{7 π}{6} + k 2 π$ .

\max y = \sqrt{3}

khi

\cos (x - \frac{π}{6}) = 1 \Leftrightarrow x = \frac{π}{6} + k 2 π

.

Câu 22:

b) Giải phương trình $\cos 3 x - \cos 4 x + \cos 5 x = 0$ .

Xem đáp án

b) Ta có $\cos 3 x - \cos 4 x + \cos 5 x = 0 \Leftrightarrow 0 \Leftrightarrow \cos 3 x + \cos 5 x = \cos 4 x$

$\Leftrightarrow 2 \cos 4 x \cos x = \cos 4 x \Leftrightarrow [\begin{array}{l} \cos 4 x = 0 \\ \cos x = \frac{1}{2} \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{π}{8} + \frac{k π}{4} \\ x = \pm \frac{π}{3} + k 2 π \end{array} (k \in ℤ)$

Câu 23:

c) Tìm tất cả các giá trị thực của tham số m để phương trình $\cos 2 x - (2 m + 1) \cos x + m + 1 = 0$ có nghiệm

trên khoảng $(\frac{π}{2}; \frac{3 π}{2})$

Xem đáp án

c) Ta có $\cos 2 x - (2 m + 1) \cos x + m + 1 = 0 \Leftrightarrow 2 \cos^{2} x - (2 m + 1) \cos x + m = 0$

$\Leftrightarrow [\begin{array}{l} \cos x = \frac{1}{2} \\ \cos x = m \end{array}$

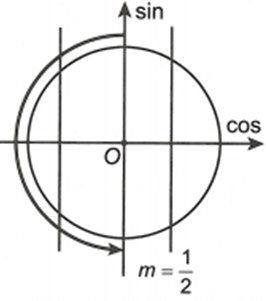
Từ hình vẽ ta thấy phương trình $\cos x = \frac{1}{2}$ không có nghiệm trên khoảng $(\frac{π}{2}; \frac{3 π}{2})$ .

Do đó yêu cầu bài toán $\Leftrightarrow \cos x = m$ có nghiệm thuộc khoảng

(\frac{π}{2}; \frac{3 π}{2}) \Leftrightarrow - 1 \leq m < 0

Câu 24:

a) Một người vào cửa hàng ăn, người đó chọn thực đơn gồm một món ăn trong 5 món, một trong 5 loại quả tráng miệng và một trong 3 loại nước uống. Có bao nhiêu cách chọn thực đơn?

Xem đáp án

a) Để chọn thực đơn, ta có

* Có 5 cách chọn món ăn.

* Có 5 cách chọn quả tráng miệng.

* Có 3 cách chọn nước uống.

Vậy theo quy tắc nhân ta có 5x5x3=75 cách.

Câu 25:

b) Chiếc kim của bánh xe trong trò chơi “Chiếc nón kì diệu” có thể dừng lại ở một trong mười vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau?

Xem đáp án

b) Số phần tử của không gian mẫu $n (Ω) = 10^{3}$

Gọi A là biến cố: “chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau”.

Lần quay 1: có 10 khả năng xảy ra.

Lần quay 2: có 9 khả năng xảy ra (không được trùng với lần quay 1).

Lần quay 3: có 8 khả năng xảy ra (không được trùng với lần quay 1, 2).

Ta có $n (A) = 10.9.8 = 720$

Vậy xác suất cần tính là

P (A) = \frac{n (A)}{n (Ω)} = \frac{720}{1000} = 0, 72

Câu 26:

c) Một trường tiểu học có 50 học sinh đạt Danh hiệu Cháu ngoan Bác Hồ, trong đó có 4 cặp anh em sinh đôi. Cần chọn một nhóm 3 học sinh trong số 50 học sinh nói trên đi dự Đại hội cháu ngoan Bác Hồ. Tính xác suất để trong nhóm được chọn không có cặp anh em sinh đôi nào.

Xem đáp án

c) Không gian mẫu $Ω$ là chọn ngẫu nhiên 3 học sinh trong số 50 học sinh.

$n (Ω) = C_{50}^{3}$

Gọi $\bar{A}$ là biến cố: “Trong 3 học sinh được chọn có một cặp anh em sinh đôi”.

Ta có

Chọn một cặp anh em sinh đôi trong 4 cặp anh em sinh đôi ta có $C_{4}^{1}$ cách.

Chọn một học sinh còn lại trong $50 - 2 = 48$ học sinh. Có 48 cách.

$\Rightarrow n (\bar{A}) = 48. C_{4}^{1}$

Suy ra

P (A) = 1 - P (\bar{A}) = 1 - \frac{n (\bar{A})}{n (Ω)} = 1 - \frac{48. C_{4}^{1}}{C_{50}^{3}} = \frac{1213}{1225}

Câu 27:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, SC.

a) Tìm giao tuyến của hai mặt phẳng (ABN) và (SCD).

Xem đáp án

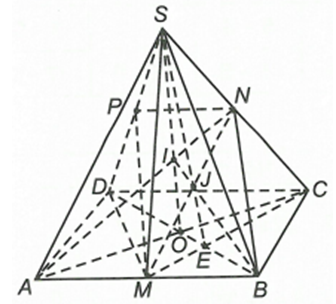
a) N là điểm chung của hai mặt phẳng (ABN) và (SCD).

Mặt khác AB // DC với $A B \subset (A B N); C D \subset (S C D)$ nên giao tuyến của hai mặt

Qua N kẻ đường thẳng song song với CD cắt SD tại P.

Suy ra giao tuyến của hai mặt phẳng (ABN) và (SCD) là đường thẳng PN.

Câu 28:

b) Chứng minh đường thẳng BN song song với mặt phẳng (SDM).

Xem đáp án

b) Ta có PN là đường trung bình của ∆SCD nên PN // CD và $P N = \frac{1}{2} C D$

Do M là trung điểm AB nên MB // CD và $M B = \frac{1}{2} C D$

Từ đó suy ra MPNP là hình bình hành => MP // NB.

Mà $M P \subset (S D M); N B ⊄ (S D M)$ nên NB // (SDM).

Vậy NB // (SDM).

Câu 29:

c) Xác định các điểm I, J lần lượt là giao điểm của đường thẳng AN và đường thẳng MN với mặt phẳng (SBD).

Xem đáp án

c) Trên mặt phẳng (ABCD), AC cắt BD tại O.

Trên mặt phẳng (SAC), PN cắt SO tại I.

Có $I \in S O \subset (S B D); I \in A N$

Vậy I là giao điểm của AN và (SBD).

Tương tự, E là giao điểm của BD và MC.

J là giao điểm SE và MN.

Khi đó J chính là giao điểm của MN và (SBD)

Câu 30:

d) Tính tỉ số $\frac{I B}{I J}$

Xem đáp án

d) Ta có I, J, B thẳng hàng do chúng cùng thuộc giao tuyến của hai mặt phẳng (SBD) và (ABN).

Trong tam giác SAC có AN, SO là hai trung tuyến nên I là trọng tâm.

Trong tam giác ABC có BO, CM là hai đường trung tuyến nên E là trọng tâm.

Xét tam giác BOI có E, J, S thẳng hàng nên

\frac{E O}{E B} . \frac{J B}{J I} . \frac{S I}{S O} = 1 \Leftrightarrow \frac{1}{2} . \frac{J B}{J I} . \frac{2}{3} = 1 \Leftrightarrow \frac{J B}{J I} = 3

Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án

Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án (Đề 1)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương