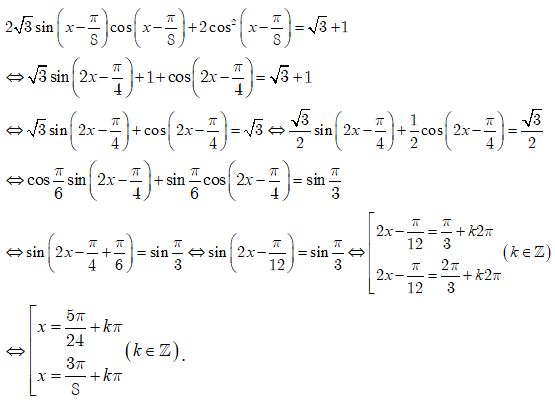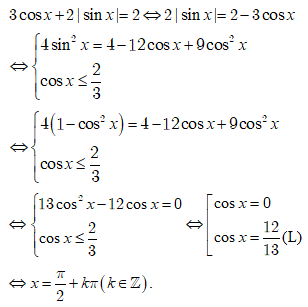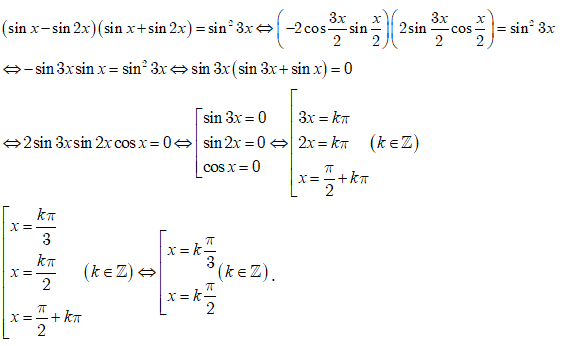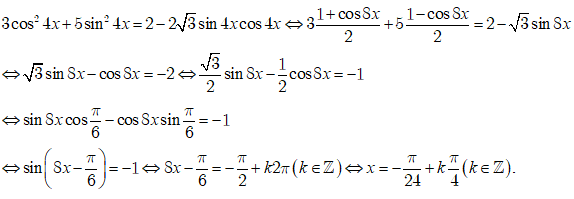20 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Phương trình lượng giác nâng cao (P5)

Câu 1:

Giải phương trình sau: 2tanx + cotx = 2sin2x + $\frac{1}{\sin 2 x}$

A. $x = - \frac{π}{4} + k 2 π; x = \pm \frac{π}{6} + k π, k \in ℤ$

B. $x = - \frac{π}{4} + \frac{k π}{2}, k \in ℤ$

C. $x = \frac{π}{3} + k π; x = \frac{π}{6} + k 2 π, k \in ℤ$

D. $x = - \frac{π}{4} + \frac{k π}{2}; x = \pm \frac{π}{6} + k π, k \in ℤ$

Xem đáp án

Đáp án D.

Điều kiện $\{\begin{cases} s inx \neq 0 \\ c o s x \neq 0 \\ \sin 2 x \neq 0 \end{cases} \Leftrightarrow \sin 2 x \neq 0 \Leftrightarrow x \neq \frac{k π}{2}, k \in ℤ$

$2 \tan x + \cot x = 2 \sin 2 x + \frac{1}{\sin 2 x}$

$\Leftrightarrow \frac{2 s {in}^{2} x + c o s^{2} x}{\cos x s inx} = \frac{2 \sin^{2} 2 x + 1}{\sin 2 x}$

$\Leftrightarrow \frac{4 s {in}^{2} x + 2 c o s^{2} x}{\sin 2 x} = \frac{2 \sin^{2} 2 x + 1}{\sin 2 x}$

$\Leftrightarrow 4 s {in}^{2} x + 2 c o s^{2} x - 2 \sin^{2} 2 x - 1 = 0$

$\Leftrightarrow 2 s {in}^{2} x - 2 \sin^{2} 2 x + 1 = 0$

$\Leftrightarrow 1 - \cos 2 x - 2 (1 - c {os}^{2} 2 x) + 1 = 0$

$\Leftrightarrow 2 c {os}^{2} 2 x - \cos 2 x = 0$

$\Leftrightarrow c os 2 x (2 \cos 2 x - 1) = 0$

$\Leftrightarrow [\begin{array}{l} c os 2 x = 0 \\ \cos 2 x = \frac{1}{2} \end{array}$

$\Leftrightarrow [\begin{array}{l} x = - \frac{π}{4} + \frac{k π}{2} \\ x = \pm \frac{π}{6} + k π \end{array}; k \in ℤ$

Vậy phương trình có nghiệm là: $x = - \frac{π}{4} + \frac{k π}{2}; x = \pm \frac{π}{6} + k π, k \in ℤ$ .

Chọn D.

Câu 2:

Giải phương trình sau: $\frac{\sin 2 x + 2 cosx - sinx - 1}{tanx + \sqrt{3}} = 0$

A. $x = \frac{π}{3} + k 2 π, k \in ℤ$

B. $x = - \frac{π}{3} + k \frac{π}{2}, k \in ℤ$

C. $x = \pm \frac{π}{3} + k 2 π, k \in ℤ$

D. Đáp án khác

Xem đáp án

Đáp án A

Điều kiện: $\{\begin{cases} \tan x \neq - \sqrt{3} \\ c o s x \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq - \frac{π}{3} + k π \\ x \neq \frac{π}{2} + k π \end{cases}, k \in ℤ$

Phương trình tương đương với: $\sin 2 x + 2 c o s x - \sin x - 1 = 0$

$\Leftrightarrow 2 \sin x c o s x + 2 c o s x - \sin x - 1 = 0$

$\Leftrightarrow 2 c o s x (\sin x + 1) - (\sin x + 1) = 0$

$\Leftrightarrow (\sin x + 1) (2 c o s x - 1) = 0$

$\Leftrightarrow [\begin{array}{l} \sin x + 1 = 0 \\ 2 c o s x - 1 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} \sin x = - 1 \\ c o s x = \frac{1}{2} \end{array}$

$\Leftrightarrow [\begin{array}{l} x = - \frac{π}{2} + k 2 π (L) \\ x = \frac{π}{3} + k 2 π (T M) \\ x = - \frac{π}{3} + k 2 π (L) \end{array}, k \in ℤ$

Vậy nghiệm của phương trình là: $x = \frac{π}{3} + k 2 π, k \in ℤ$ .

Chọn A.

Câu 3:

Giải phương trình sau: $\frac{(1 + sinx + \cos 2 x) \sin (x + \frac{π}{4})}{1 + tanx} = \frac{1}{\sqrt{2}} cosx$

A. x = $- \frac{π}{6}$ + k2π, $k \in ℤ$

B. x = $- \frac{5 π}{3}$ + k $\frac{π}{2}$ , $k \in ℤ$

C. x = $- \frac{π}{6}$ + k2π; x = $\frac{7 π}{6}$ + k2π, $k \in ℤ$

D: Đáp án khác

Xem đáp án

Điều kiện $\{\begin{cases} cos x \neq 0 \\ \tan x \neq - 1 \end{cases}$

$\frac{(1 + s inx + c os2x) \sin (x + \frac{π}{4})}{1 + \tan x} = \frac{1}{\sqrt{2}} \cos x$

$\Leftrightarrow \sqrt{2} \sin (x + \frac{π}{4}) (1 + s inx + c os2x) = \cos x (1 + \tan x)$

$\Leftrightarrow (s inx + c osx) (1 + s inx + c os2x) = \cos x . \frac{s inx + c osx}{\cos x}$

$\Leftrightarrow (s inx + c osx) (1 + s inx + c os2x) - (s inx + c osx) = 0$

$\Leftrightarrow (s inx + c osx) (s inx + c os2x) = 0$

$\Leftrightarrow [\begin{array}{l} s inx + c osx = 0 \\ s inx + c os2x = 0 \end{array}$

+) sin x + cosx = 0 thì tanx = -1 (không thỏa mãn điều kiện)

+) sin x + cos2x = 0

$\Leftrightarrow$ sinx + 1 – 2 sin² x = 0

$\Leftrightarrow [\begin{array}{l} s inx = 1 \\ s inx = - \frac{1}{2} \end{array}$

Vì sin x = 1 nên cosx = 0 (loại)

$s inx = - \frac{1}{2} \Leftrightarrow [\begin{array}{l} x = - \frac{π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{array}, k \in ℤ$

Vậy phương trình đã cho có nghiệm $x = - \frac{π}{6} + k 2 π, x = \frac{7 π}{6} + k 2 π, k \in ℤ$ .

Chọn C.

Câu 4:

Giải phương trình sau: $\frac{(1 - 2 sinx) cosx}{(1 + 2 sinx) (1 - sinx)} = \sqrt{3}$

A. x = $- \frac{π}{18}$ + kπ, $k \in ℤ$

B. x = $- \frac{π}{18}$ + k $\frac{2 π}{3}$ , $k \in ℤ$

C. x = $- \frac{π}{6}$ + kπ; $- \frac{π}{18}$ + kπ, $k \in ℤ$

D: Đáp án khác

Xem đáp án

Đáp án B

Câu 5:

Giải phương trình sau: $\frac{1}{sinx} + \frac{1}{\sin (x - \frac{3 π}{2})} = 4 \sin (\frac{7 π}{4} - x)$

A. x = $- \frac{π}{8}$ + kπ

B. x = $- \frac{π}{4}$ + kπ

C. x = $- \frac{π}{4}$ + kπ, $- \frac{π}{8}$ + kπ; $\frac{5 π}{8}$ + kπ

D: Đáp án khác

Xem đáp án

Đáp án C

Câu 6:

Giải phương trình sau: $2 \sqrt{3} \sin (x - \frac{π}{8}) \cos (x - \frac{π}{8}) + 2 \cos^{2} (x - \frac{π}{8}) = \sqrt{3} + 1$

A.

B.

C.

D: Giải phương trình sau: 2căn(3)sin(x - pi/8)cos(x - pi/8) + 2cos^2(x - pi/8) = căn(3) + 1: A.x=3pi/5+kpi hoặc x=5pi/24+kpi (ảnh 5)

Xem đáp án

Đáp án A

Câu 7:

Phương trình 3cosx + 2|sin x| = 2 có nghiệm là:

A. x = $\frac{π}{8}$ + kπ

B. x = $\frac{π}{6}$ + kπ

C. x = $\frac{π}{4}$ + kπ

D. x = $\frac{π}{2}$ + kπ

Xem đáp án

Đáp án D

Câu 8:

Phương trình: (sinx - sin2x)(sinx + sin2x) = sin²3x có các nghiệm là:

A.

B.

C.

D.

Xem đáp án

Đáp án A

Câu 9:

Phương trình: 3cos²4x + 5sin²4x = 2 – 2 $\sqrt{3}$ sin4x.cos4x có nghiệm là:

A. x = $- \frac{π}{6}$ + kπ

B. x = $- \frac{π}{12}$ + k $\frac{π}{2}$

C. x = $- \frac{π}{18}$ + k $\frac{π}{3}$

D. x = $- \frac{π}{24}$ + k $\frac{π}{4}$

Xem đáp án

Đáp án D

Câu 10:

Phương trình $cosx + sinx = \frac{\cos 2 x}{1 - \sin 2 x}$ có nghiệm là:

A. $[\begin{array}{l} x = - \frac{π}{4} + k 2 π \\ x = \frac{π}{8} + k π \\ x = k \frac{π}{2} \end{array}, k \in ℤ$

B. $[\begin{array}{l} x = \frac{π}{4} + k 2 π \\ x = \frac{π}{2} + k π \\ x = k π \end{array}, k \in ℤ$

C. $[\begin{array}{l} x = \frac{3 π}{4} + k 2 π \\ x = - \frac{π}{2} + k π \\ x = k 2 π \end{array}, k \in ℤ$

D. $[\begin{array}{l} x = \frac{5 π}{4} + k 2 π \\ x = \frac{3 π}{8} + k π \\ x = k \frac{π}{4} \end{array}, k \in ℤ$

Xem đáp án

Đáp án C

Câu 11:

Phương trình sin²3x – cos²4x = sin²5x – cos²6x có các nghiệm là:

A. $x = k \frac{π}{12}, x = k \frac{π}{4}, k \in ℤ$

B. $x = k \frac{π}{9}, x = k \frac{π}{2}, k \in ℤ$

C. $x = k \frac{π}{6}, x = k π, k \in ℤ$

D. $x = k \frac{π}{3}, x = k 2 π, k \in ℤ$

Xem đáp án

Đáp án B

Câu 12:

Phương trình: 4sinx.sin(x + $\frac{π}{3}$ ).sin(x + $\frac{2 π}{3}$ ) + cos3x = 1 có các nghiệm là:

A.

B.

C.

D.

Xem đáp án

Đáp án A

Câu 13:

Giải phương trình tanx + tan2x = -sin3x.cos2x.

A. x = k $\frac{π}{3}$ ; x = π + k2π

B. x = k $\frac{π}{3}$ ; x = $\frac{π}{2}$ + k2π

C. x = k $\frac{π}{3}$

D. x = k2π

Xem đáp án

Đáp án C

Do đó, từ (*) suy ra:

Kết hợp 2 trường hợp và điều kiện, suy ra nghiệm của phương trình đã cho là $x = \frac{k π}{3}$

Câu 14:

Giải phương trình tan( $\frac{π}{3}$ - x).tan( $\frac{π}{3}$ + 2x) = 1

A. x = $\frac{π}{6}$ + kπ

B. x = $- \frac{π}{3}$ + kπ

C. x = $- \frac{π}{6}$ + kπ

D. Vô nghiệm

Xem đáp án

Đáp án D

Vậy phương trình đã cho vô nghiệm

Câu 15:

Giải phương trình: $8 \cot 2 x = \frac{(\cos^{2} x - \sin^{2} x) . \sin 2 x}{\cos^{6} x + \sin^{6} x}$

A. x = $- \frac{π}{4}$ + kπ

B. x = ± $\frac{π}{4}$ + k $\frac{π}{2}$

C. x = $\frac{π}{4}$ + kπ

D. x = $\frac{π}{4}$ + k $\frac{π}{2}$

Xem đáp án

Đáp án D

Ta có:

Câu 16:

Phương trình tanx + tan(x + $\frac{π}{3}$ ) + tan(x + $\frac{2 π}{3}$ ) = 3 $\sqrt{3}$ tương đương với phương trình.

A. cot x = $\sqrt{3}$

B. cot 3x = $\sqrt{3}$

C. tan x = $\sqrt{3}$

D. tan 3x = $\sqrt{3}$

Xem đáp án

Đáp án D

Câu 17:

Tìm số nghiệm thuộc khoảng ( $\frac{π}{2}$ ; 3π) của phương trình:

sin(2x + $\frac{5 π}{2}$ ) - 3cos(x - $\frac{7 π}{2}$ ) = 1 + 2sinx (*)

A: 3

B: 4

C: 5

D: 6

Xem đáp án

Đáp án C

Câu 18:

Phương trình $\frac{(1 - 2 cosx) (1 + cosx)}{(1 + 2 cosx) . sinx} = 1$ có bao nhiêu nghiệm thuộc khoảng (0; 2018π)

A: 3017

B: 3027

C: 3037

D: 3047

Xem đáp án

Đáp án B

Câu 19:

Các nghiệm của phương trình $2 (1 + cosx) (1 + \cot^{2} x) = \frac{sinx - 1}{sinx + cosx}$ được biểu diễn bởi bao nhiêu điểm trên đường tròn lượng giác?