100 câu trắc nghiệm Phương trình lượng giác nâng cao (P2)
-
356 lượt thi
-
20 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Hàm số y = 2cos2 x + 3cos3x + 8cos4x tuần hoàn với chu kì
 Xem đáp án
Xem đáp án
Đáp án B
+ Hàm số y = 9/4cos x tuần hoàn với chu kì 2π.
+ Hàm số y = 5cos 2x tuần hoàn với chu kì 2π/2 = π .
+ Hàm số y = 3/4 cos 3x tuần hoàn với chu kì 2π/3.
+ Hàm số y = cos 4x tuần hoàn với chu kì 2π/4 = π/2.
+ Do đó hàm số y = 2 cos2 x + 3cos3x + 8cos4x là hàm tuần hoàn với chu kì 2π.
Chú ý:

Câu 2:
Hàm số y = 2sin2x + 4cos2x + 6sinxcosx tuần hoàn với chu kì:
 Xem đáp án
Xem đáp án
Đáp án C
+ Hàm số y = 3sin 2x tuần hoàn với chu kì 2π/2 = π.
+ Hàm số y = cos 2x tuần hoàn với chu kì 2π/2 = π.
+ Do đó hàm số y = 2sin2x + 4cos2x + 6sinxcosx là hàm tuần hoàn với chu kì π
Câu 3:
Tìm tất cả các giá trị của tham số m để hàm số sau chỉ nhận giá trị dương :
y = (3sinx - 4cosx)2 - 6sinx + 8cosx + 2m - 1
 Xem đáp án
Xem đáp án
Đáp án B
Đặt t = 3sin x - 4 cos x => -5 ≤ t ≤ 5
Ta có: y = t2 – 2t + 2m – 1 = (t – 1)2 + 2m - 2
Với mọi t ta có (t – 1)2 ≥ 0 nên y ≥ 2m - 2 => min y = 2m - 2
Hàm số chỉ nhận giá trị dương ⇔ y > 0 ∀x ∈ R ⇔ min y > 0
⇔ 2m - 2 > 0 ⇔ m > 1

Câu 4:
Tìm m để hàm số y = xác định với mọi x
 Xem đáp án
Xem đáp án
Đáp án D
Hàm số xác định với mọi x
⇔ 2sin2x + 4sinx cosx – (3 + 2m)cos2x + 2 0 ∀x ∈ R (1)
cos x = 0 => (1) đúng
cos x ≠ 0 khi đó ta có: (1) ⇔ 2tan2x + 4tanx – (3 + 2m) + 2(1 + tan2x) ≥ 0
⇔ 4tan2x + 4tanx ≥ 1 + 2m ∀x ∈ R
⇔ (2tanx + 1)2 ≥ 2 + 2m ∀x ∈ R ⇔ 2 + 2m ≤ 0 ⇔ m ≤ -1
Câu 6:
Tìm m để các bất phương trình sau đúng với mọi x:
(3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1
 Xem đáp án
Xem đáp án
Đáp án D
Đặt t = 3sin x - 4cos x
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 1)2 -1
Với mọi t ta có; => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.
Câu 10:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: y = sin6x + cos6x
 Xem đáp án
Xem đáp án
Đáp án C
Câu 12:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y = tanx, x ∈ [; ]
 Xem đáp án
Xem đáp án
Đáp án D
![Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y = tanx, x thuộc [-pi/3; pi/6]: A.maxy=căn 3/3; miny=1/3 (ảnh 1)](https://video.vietjack.com/upload1/quiz_source1/2019/09/p2-c12-1567703369.png)
Câu 16:
Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án B
![Khẳng định nào sau đây là đúng ? A.y = |tan x| đồng biến trong [-pi/2;pi/2] B.y = |tan x| là hàm số chẵn trên D=R (ảnh 1)](https://video.vietjack.com/upload1/quiz_source1/2019/07/p2-c16-1562512660.png)
Ta được đồ thị như hình vẽ trên.
Ta thấy hàm số y = |tan x| nghịch biến trên (-π/2; 0) và đồng biến trên (0; π/2) . Nên ta loại A và D.
Với B ta có f(-x) = |tan(-x)| = | - tan x |= |tan x| = f(x) => hàm số y = |tan x| là hàm số chẵn.
Hàm số chẵn, nhận trục Oy làm trục đối xứng, không nhận tâm O làm tâm đối xứng.
Nên phương án C là sai

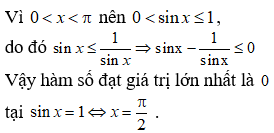

![Cho hàm số sau y = tan^2x – tanx + 2, x [-pi/4;pi/4]. Chọn khẳng định đúng: A.max y=căn 3/3 B.maxy=4 (ảnh 1)](https://video.vietjack.com/upload1/quiz_source1/2019/09/p2-c13-1567703532.png)
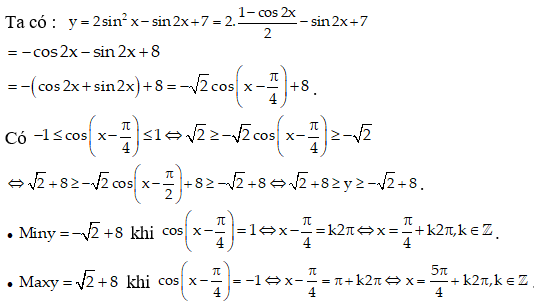

![Tìm tổng các nghiệm của phương trình: sin(5x + pi/3) = cos(2x - pi/3) trên [0; pi] (ảnh 1)](https://video.vietjack.com/upload1/quiz_source1/2019/09/p2-c20-1567704196.png)