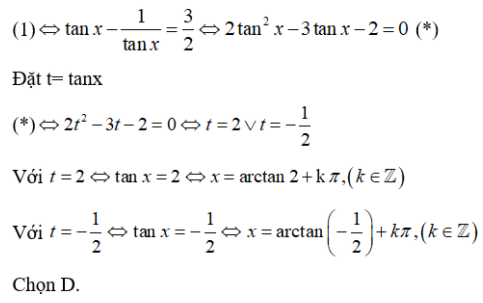27 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Hàm số lượng giác cơ bản (P3)

Câu 1:

Giải phương trình sau: cos 2x - 3sin x - 2 = 0

Giải phương trình sau: cos2x - 3sinx - 2 = 0: A.-pi/2+k2pi B.-pi/6+k2pi C.-7pi/6+kpi/2 D.Đáp án khác (ảnh 5)

Xem đáp án

Câu 2:

Giải phương trình sau: $\frac{1}{\sin^{2} x} = c o t x + 3$

A. $x = - \frac{π}{4} + k π, x = arccot 2 + k π, k \in ℤ$

B. $x = - \frac{π}{4} + k 2 π, k \in ℤ$

C. $x = \frac{5 π}{3} + k 2 π, k \in ℤ$

D. Tất cả sai

Xem đáp án

Câu 3:

Giải phương trình sau: $\tan x - c o t x = \frac{3}{2}$

A. $x = - \frac{π}{2} + k 2 π, k \in ℤ$

B. $x = \arctan (- \frac{1}{2}) + k π, k \in ℤ$

C. x = arctan(2)

D. Đáp án khác

Xem đáp án

Điều kiện: $\{\begin{cases} \sin x \neq 0 \\ \cos x \neq 0 \end{cases} \Leftrightarrow \sin 2 x \neq 0 \Leftrightarrow x \neq k \frac{π}{2},$ $k \in ℤ$

Câu 4:

Giải phương trình sau: $\cos^{3} x + 3 \cos^{2} x + 2 \cos x = 0$

Giải phương trình sau cos^3(x) - 3cos^2(x) - 2cosx = 0: A.-pi/2+k2pi B.x=arctan(-1/2)+kpi,k thuộc Z (ảnh 3)

Xem đáp án

Câu 5:

Giải phương trình sau: 23sin x - sin 3x = 24

Giải phương trình sau 23sinx - sin3x = 24: A.-pi/2+k2pi B.pi/2+k2pi C.x=pi/2+kpi;x=k2pi,k khác Z D.Đáp án khác (ảnh 5)

Xem đáp án

Đặt t = sinx ; $(- 1 \leq t \leq 1)$

Câu 6:

Giải phương trình sau: $2 \cos 3 x . \cos x - 4 \sin^{2} 2 x + 1 = 0$

Giải phương trình sau 2cos(3x) * cos(x) - 4sin^2(2x) + 1=0: A. cộng trừ pi/6+k2pi B.pi/6+kpi (ảnh 2)

Giải phương trình sau 2cos(3x) * cos(x) - 4sin^2(2x) + 1=0: A. cộng trừ pi/6+k2pi B.pi/6+kpi (ảnh 3)

Giải phương trình sau 2cos(3x) * cos(x) - 4sin^2(2x) + 1=0: A. cộng trừ pi/6+k2pi B.pi/6+kpi (ảnh 4)

Xem đáp án

Câu 7:

Phương trình cot3x = cotx có mấy nghiệm thuộc

A. 9

B. 20

C. 19

D. 10

Xem đáp án

Câu 8:

Giải phương trình $5 \cos x - 2 \sin \frac{x}{2} + 7 = 0$

Xem đáp án

Câu 9:

Giải phương trình $\cos 4 x + 12 \sin x . \cos x - 5 = 0$

Giải phương trình cos(4x) + 12 sin(x)*cos(x) - 5 = 0: A.pi/4+k2pi B.pi+k4pi C.pi/4+kpi D.Tất cả sai (ảnh 3)

Giải phương trình cos(4x) + 12 sin(x)*cos(x) - 5 = 0: A.pi/4+k2pi B.pi+k4pi C.pi/4+kpi D.Tất cả sai (ảnh 5)

Xem đáp án

Câu 10:

Giải phương trình: $\frac{3}{\sin^{2} x} - 2 \sqrt{3} c o t x - 6 = 0$

Giải phương trình: 3 * (1 + cot^2(x) - (2căn3)cotx - 6 = 0: A.-pi/6+k2pi B.pi/3+kpi C.pi/6+kpi;-pi/3+kpi D.Tất cả sai (ảnh 3)

Giải phương trình: 3 * (1 + cot^2(x) - (2căn3)cotx - 6 = 0: A.-pi/6+k2pi B.pi/3+kpi C.pi/6+kpi;-pi/3+kpi D.Tất cả sai (ảnh 5)

Xem đáp án

Chọn C

Câu 11:

Giải phương trình: $\cos 2 x - 3 \cos x = 4 \cos^{2} \frac{x}{2}$

Giải phương trình cos(2x) - 3cosx = 4cos^2(x/2) (ảnh 1)

Giải phương trình cos(2x) - 3cosx = 4cos^2(x/2) (ảnh 3)

Giải phương trình cos(2x) - 3cosx = 4cos^2(x/2) (ảnh 4)

Xem đáp án

$cos2x - 3cosx = 4 \cos^{2} \frac{x}{2}$

$\Leftrightarrow 2 {cos}^{2} x - 1 - 3cosx = 4. \frac{1 + c os x}{2}$

$\Leftrightarrow 2 \cos^{2} x - 5 \cos x - 3 = 0$

$\Leftrightarrow [\begin{array}{l} cos x = - \frac{1}{2} (T M D K) \\ \cos x = 3 (K T M D K) \end{array}$

$\Leftrightarrow cos x = - \frac{1}{2}$

$\Leftrightarrow c os x = c os \frac{2 π}{3}$

$\Leftrightarrow x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ$

Chọn D.

Câu 12:

Phương trình $(\sin x + 1) (\sin x - \sqrt{2}) = 0$ có nghiệm là:

Phương trình (sinx +1) * (sinx - căn 2) = 0 có nghiệm là: A.x=-pi/2+k2pi(k thuộc Z) B.x=cộng trừ pi/4+k2pi,x=-pi/8+kpi(k thuộc Z) (ảnh 3)

Phương trình (sinx +1) * (sinx - căn 2) = 0 có nghiệm là: A.x=-pi/2+k2pi(k thuộc Z) B.x=cộng trừ pi/4+k2pi,x=-pi/8+kpi(k thuộc Z) (ảnh 5)

Xem đáp án

Câu 13:

Phương trình $2 \sin^{2} x + \sin x \cos x - \cos^{2} x = 0$ có nghiệm là:

Phương trình 2 sin^2(x) + sinx*cosx - cos^2(x) = 0 có nghiệm là:A.pi/4+kpi B.pi/4+kpi,arctan(1/2)+kpi (ảnh 2)

Phương trình 2 sin^2(x) + sinx*cosx - cos^2(x) = 0 có nghiệm là:A.pi/4+kpi B.pi/4+kpi,arctan(1/2)+kpi (ảnh 3)

Phương trình 2 sin^2(x) + sinx*cosx - cos^2(x) = 0 có nghiệm là:A.pi/4+kpi B.pi/4+kpi,arctan(1/2)+kpi (ảnh 4)

Phương trình 2 sin^2(x) + sinx*cosx - cos^2(x) = 0 có nghiệm là:A.pi/4+kpi B.pi/4+kpi,arctan(1/2)+kpi (ảnh 5)

Xem đáp án

Câu 14:

Một họ nghiệm của phương trình $2 \sin^{2} x - 5 \sin x \cos x - \cos^{2} x = - 2$ là:

Xem đáp án

+ Khi cosx = 0 thì $c o s^{2} x = 0 \Rightarrow \sin^{2} x = 1$ . Thay vào phương trình đã cho ta được :

$2.1 - 5.0 - 0^{2} = - 2$ ( vô lí)

Do đó, cosx $\neq 0$ .

Câu 15:

Giải phương trình $4 \sin^{3} x + 3 \cos^{3} x - 3 \sin x - \sin^{2} x \cos x = 0$

Giải phương trình 4sin^3(x )- 3cos^3(x) - 3sinx - sin^2(x)*cos(x)-0: A.x=pi/4+k2pi,x= cộng trừ pi/3+k2pi (ảnh 2)

Giải phương trình 4sin^3(x )- 3cos^3(x) - 3sinx - sin^2(x)*cos(x)-0: A.x=pi/4+k2pi,x= cộng trừ pi/3+k2pi (ảnh 3)

Giải phương trình 4sin^3(x )- 3cos^3(x) - 3sinx - sin^2(x)*cos(x)-0: A.x=pi/4+k2pi,x= cộng trừ pi/3+k2pi (ảnh 4)

Giải phương trình 4sin^3(x )- 3cos^3(x) - 3sinx - sin^2(x)*cos(x)-0: A.x=pi/4+k2pi,x= cộng trừ pi/3+k2pi (ảnh 5)

Xem đáp án

Ta thấy cosx =0 không là nghiệm của phương trình đã cho.

Chia cả hai vế của phương trình cho $\cos^{3} x \neq 0$ ta được:

chọn D

Câu 16:

Giải phương trình $\tan (2 x + \frac{π}{6}) + \tan (\frac{π}{3} - x) = 0$

Giải phương trình tan(2x+pi/6) + tan(pi/3-x) = 0: A.x=-pi/2+kpi(k thuộc Z) B.x= cộng trừ pi/4+k2pi,x=-pi/8+kpi(k thuộc Z) (ảnh 5)

Xem đáp án

Câu 17:

Giải phương trình $\tan (x - \frac{π}{6}) - c o t (\frac{π}{3} + x) = 0$

Giải phương trình tan(x-pi/6)- cot(pi/3 + x) = 0: A.x=-pi/6+kpi(k thuộc Z) B.x= cộng trừ pi/6+k2pi,x=-pi/8+kpi(k thuộc Z) (ảnh 4)

Giải phương trình tan(x-pi/6)- cot(pi/3 + x) = 0: A.x=-pi/6+kpi(k thuộc Z) B.x= cộng trừ pi/6+k2pi,x=-pi/8+kpi(k thuộc Z) (ảnh 7)

Xem đáp án

Kết hợp điều kiện, vậy nghiệm của phương trình đã cho là $x = \frac{π}{6} + k π$

chọn C.

Câu 18:

Tìm số nghiệm của phương trình $\cos 2 x + \sin x = 0$ trong khoảng

A. Vô nghiệm

B. 1

C. 2

D. 3

Xem đáp án

Câu 19:

Giải phương trình $2 \sin^{2} x + \sqrt{3} \sin 2 x = 3$

Giải phương trình 2 sin^2(x) + Căn3 sin(2x) = 3: A.x=-pi/3+kpi B.x=pi/3+kpi C.x=2pi/3+k2pi D.x=pi/4+kpi (ảnh 3)

Giải phương trình 2 sin^2(x) + Căn3 sin(2x) = 3: A.x=-pi/3+kpi B.x=pi/3+kpi C.x=2pi/3+k2pi D.x=pi/4+kpi (ảnh 4)

Xem đáp án

Câu 20:

Tổng tất cả các nghiệm của phương trình $\sin 3 x - \frac{2}{\sqrt{3}} \sin^{2} x = 2 \sin x \cos 2 x$ thuộc $[0; π]$

A. 5 $π$

B. 6 $π$

C. 3 $π$

D. 2 $π$

Xem đáp án

Câu 21:

Số nghiệm của phương trình $\cos x = \frac{1}{2}$ thuộc $[- 2 π; 2 π]$

A. 4

B. 2

C.3

D.1

Xem đáp án

Câu 22:

Cho phương trình $3 - \sqrt{3} \tan (2 x - \frac{π}{3}) = 0$ với $\frac{- π}{4} < x < \frac{2 π}{3}$ tìm khẳng định đúng?

A. Có 1 nghiệm thỏa mãn

B. Có 2 nghiệm thỏa mãn

C. Có 2 nghiệm âm

D. Có 3 nghiệm dương

Xem đáp án

Câu 23:

Giải phương trình $(c o t \frac{x}{3} - 1) (c o t \frac{x}{2} + 1) = 0$

Xem đáp án

Câu 24:

Giải phương trình $\tan (x - 30 °) \cos (2 x - 150 °) = 0$

Giải phương trình tan(x-30) * cos(2x-150) = 0 (ảnh 1)

B. $x = \pm \frac{π}{6} + k 2 π, x = \frac{π}{2} + k π, k \in ℤ$

C. $x = \frac{π}{6} + k π, k \in ℤ$

D. Đáp án khác

Xem đáp án

tan(3x – 30⁰).cos(2x – 150⁰) = 0

$\Leftrightarrow \tan (x - \frac{π}{6}) . \cos (2 x - \frac{5 π}{6}) = 0$

Điều kiện: $cos (x - \frac{π}{6}) \neq 0$ (*)

$\Leftrightarrow [\begin{array}{l} \tan (x - \frac{π}{6}) = 0 \\ \cos (2 x - \frac{5 π}{6}) = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x - \frac{π}{6} = k π \\ 2 x - \frac{5 π}{6} = \frac{π}{2} + k 2 π \\ 2 x - \frac{5 π}{6} = - \frac{π}{2} + k 2 π \end{array}, k \in ℤ$