Giải SGK Toán 7 Bài 2 (Chân trời sáng tạo): Số thực. Giá trị tuyệt đối của một số thực

Giải SGK Toán 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực

Hoạt động khởi động

Giải Toán 7 trang 35 Tập 1

Khởi động trang 35 Toán lớp 7 Tập 1: Người ta gọi tập hợp các số hữu tỉ và số vô tỉ là gì?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Tập hợp gồm các số hữu tỉ và số vô tỉ là tập số thực.

1. Số thực và tập hợp các số thực

Khám phá 1 trang 35 Toán lớp 7 Tập 1: Trong các số sau, số nào là số hữu tỉ, số nào là số vô tỉ?

$\frac{2}{3};3,\left(45\right);\sqrt{2};-45;-\sqrt{3};0;\pi .$

Lời giải:

Các số là số hữu tỉ là $\frac{2}{3};3,\left(45\right);-45;0$.

Các số là số vô tỉ là $\sqrt{2};-\sqrt{3};\pi$.

Thực hành 1 trang 35 Toán lớp 7 Tập 1: Các khẳng định sau đúng hay sai? Nếu sai, hãy phát biểu lại cho đúng.

a) $\sqrt{3}\in \mathbb{Q}$;

b) $\sqrt{3}\in ℝ$;

c) $\frac{2}{3}\notin ℝ$;

d) $-9\in ℝ$.

Lời giải:

a) $\sqrt{3}$ là số vô tỉ nên $\sqrt{3}\notin \mathbb{Q}$ do đó khẳng định $\sqrt{3}\in \mathbb{Q}$ sai.

Phát biểu đúng: $\sqrt{3}\notin \mathbb{Q}$ hoặc $\sqrt{3}\in \mathrm{𝕀}$ hoặc $\sqrt{3}\in ℝ.$

b) $\sqrt{3}$ là số vô tỉ nên khẳng định $\sqrt{3}\in ℝ$ đúng.

c) $\frac{2}{3}$ là số hữu tỉ nên khẳng định $\frac{2}{3}\notin ℝ$ sai.

Phát biểu đúng:$\frac{2}{3}\in ℝ$ hoặc $\frac{2}{3}\in \mathbb{Q}$ hoặc $\frac{2}{3}\notin \mathrm{𝕀}.$

d) –9 là số nguyên nên khẳng định $-9\in ℝ$ đúng.

2. Thứ tự trong tập hợp các số thực

Khám phá 2 trang 35 Toán lớp 7 Tập 1: Hãy so sánh các số thập phân sau đây: 3,14; 3,1415; 3,141515.

Lời giải:

Ta có 3,14 = 3,140000;  3,1415 = 3,141500.

Do 3,140000 < 3,141500 < 3,141515 nên 3,14 < 3,1415 < 3,141515.

Vậy 3,14 < 3,1415 < 3,141515.

Giải Toán 7 trang 36 Tập 1

Thực hành 2 trang 36 Toán lớp 7 Tập 1: So sánh hai số thực:

a) 4,(56) và 4,56279;

b) –3,(65) và –3,6491;

c) 0,(21) và 0,2(12);

d) $\sqrt{2}$ và 1,42.

Lời giải:

a) Ta có: 4,(56) = 4,565656…

Do 4,565656… > 4,56279 nên 4,(56) > 4,56279.

b) Ta có: –3,(65) = –3,6565…

Do 3,6565… > 3,6491 nên –3,6565… < –3,6491.

Vậy –3,(65) < –3,6491.

c) Ta có: 0,(21) = 0,212121…;  0,2(12) = 0,212121…

Do 0,212121… = 0,212121… nên 0,(21) = 0,2(12).

d) Ta có: $\sqrt{2}\approx 1,\mathrm{414213562...}$

Do 1,414213562… < 1,42 nên $\sqrt{2}<1,42.$

Vận dụng 1 trang 36 Toán lớp 7 Tập 1: Cho một hình vuông có diện tích 5 m². Hãy so sánh độ dài a của cạnh hình vuông đó với độ dài b = 2,361 m.

Lời giải:

Độ dài a của cạnh hình vuông bằng $\sqrt{5}$ m.

Ta có: $\sqrt{5}=2,\mathrm{236067977...}$

Do 2,236067977… < 2,361 nên độ dài a của cạnh hình vuông nhỏ hơn độ dài b.

3. Trục số thực

Khám phá 3 trang 36 Toán lớp 7 Tập 1: Quan sát hình vẽ bên và cho biết độ dài của đoạn thẳng OA bằng bao nhiêu.

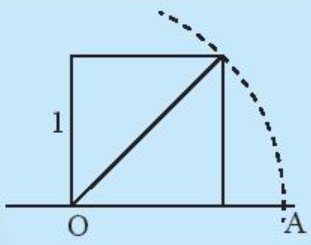
Độ dài OA có là số hữu tỉ hay không?

Lời giải:

Độ dài của đoạn thẳng OA bằng độ dài đường chéo trong hình vuông.

Hình vuông có cạnh bằng 1 thì độ dài đường chéo là $\sqrt{2}.$

Do đó độ dài đoạn thẳng OA bằng $\sqrt{2}.$

Số $\sqrt{2}$ không phải số hữu tỉ nên độ dài đoạn thẳng OA không phải số hữu tỉ.

Thực hành 3 trang 36 Toán lớp 7 Tập 1: Hãy biểu diễn các số thực: –2; $-\sqrt{2};$–1,5; 2; 3 trên trục số.

Lời giải:

Do –2 < 0; –1,5 < 0 và $-\sqrt{2}$ < 0 nên điểm –2, điểm $-\sqrt{2}$ và điểm –1,5 nằm ở bên trái điểm 0.

Do 2 > 0 và 3 > 0 nên điểm 2, điểm 3 nằm ở bên phải điểm 0.

+) Ta biểu diễn các điểm –2; 2; 3 như sau:

Do –2 < 0 nên điểm –2 nằm ở bên trái điểm 0 và cách điểm 0 một khoảng bằng 2 lần đoạn thẳng đơn vị.

Do 2 > 0 nên điểm 2 nằm ở bên phải điểm 0 và cách điểm 0 một khoảng bằng 2 lần đoạn thẳng đơn vị.

Do 3 > 0 nên điểm 3 nằm ở bên phải điểm 0 và cách điểm 0 một khoảng bằng 3 lần đoạn thẳng đơn vị.

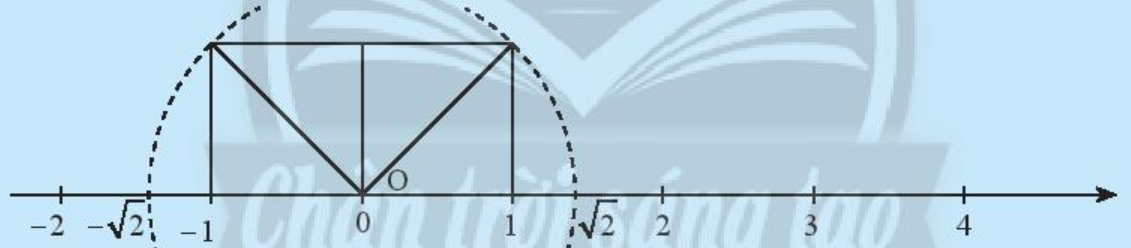
+) Ta biểu diễn điểm $-\sqrt{2}$ như sau:

Ở bên trái điểm O, vẽ hình vuông có cạnh là 1, khi đó độ dài đường chéo bằng $\sqrt{2}.$

Thực hiện vẽ cung tròn có tâm tại điểm 0, bán kính $\sqrt{2}.$ Cung tròn này cắt trục số tại điểm $-\sqrt{2}.$

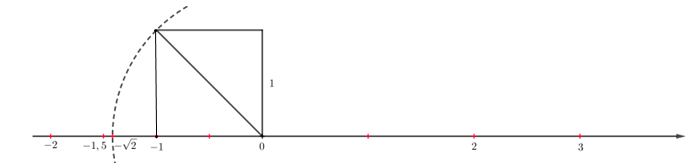
+) Ta biểu diễn điểm –1,5 như sau:

Chia đoạn thẳng đơn vị thành 2 đoạn bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng $\frac{1}{2}=0,5$ đơn vị cũ.

Do –1,5 < 0 nên điểm –1,5 nằm ở bên trái điểm 0 và cách 0 một khoảng bằng 3 lần đơn vị mới.

Ta có hình vẽ như sau:

Vận dụng 2 trang 36 Toán lớp 7 Tập 1: Không cần vẽ hình, hãy nêu nhận xét về vị trí của hai số $\sqrt{2};\frac{3}{2}$ trên trục số.

Lời giải:

Do $\sqrt{2}>0$ và $\frac{3}{2}>0$ nên điểm $\sqrt{2};\frac{3}{2}$ nằm ở bên phải điểm 0.

Ta có $\sqrt{2}\approx 1,\mathrm{414213562...}$;  $\frac{3}{2}=1,5.$

Do 1,414213562… < 1,5 nên $\sqrt{2}<\frac{3}{2}.$

Do đó điểm $\sqrt{2}$ nằm ở bên trái điểm $\frac{3}{2}.$

Vậy trên trục số, hai điểm $\sqrt{2}$ và $\frac{3}{2}$ cùng nằm bên phải điểm 0, điểm $\sqrt{2}$ ở bên trái điểm $\frac{3}{2}$.

4. Số đối của một số thực

Giải Toán 7 trang 37 Tập 1

Khám phá 4 trang 37 Toán lớp 7 Tập 1:

Gọi A và A’ lần lượt là các điểm biểu diễn hai số 4,5 và –4,5 trên trục số. So sánh OA và OA’.

Lời giải:

Độ dài đoạn thẳng OA là 4,5 đơn vị.

Độ dài đoạn thẳng OA’ là 4,5 đơn vị.

Do đó, độ dài OA bằng với độ dài OA’.

Thực hành 4 trang 37 Toán lớp 7 Tập 1: Tìm số đối của các số thực sau: 5,12; $\pi ;-\sqrt{13}$.

Lời giải:

Số đối của số 5,12 là –5,12.

Số đối của số π là số $-\pi$.

Số đối của $-\sqrt{13}$ là $-\left(-\sqrt{13}\right)=\sqrt{13}.$

Vận dụng 3 trang 37 Toán lớp 7 Tập 1: So sánh các số đối của hai số $\sqrt{2}$ và $\sqrt{3}$.

Lời giải:

Ta có:

Số đối của $\sqrt{2}$ là $-\sqrt{2}$.

Số đối của $\sqrt{3}$ là $-\sqrt{3}$.

Do $\sqrt{2}<\sqrt{3}$ nên $-\sqrt{2}>-\sqrt{3}.$

5. Giá trị tuyệt đối của một số thực

Khám phá 5 trang 37 Toán lớp 7 Tập 1: Trên trục số, so sánh khoảng cách từ điểm 0 đến hai điểm $\sqrt{2}$ và $-\sqrt{2}$.

Lời giải:

Trên trục số, khoảng cách từ điểm 0 đến điểm $\sqrt{2}$ bằng khoảng cách từ điểm 0 đến điểm $-\sqrt{2}.$

Thực hành 5 trang 37 Toán lớp 7 Tập 1: Tìm giá trị tuyệt đối của các số thực sau: –3,14;   41;   –5;    1,(2);    $-\sqrt{5}.$

Lời giải:

Do –3,14 < 0 nên $\left|-3,14\right|$ = –(–3,14) = 3,14.

Do 41 > 0 nên $\left|41\right|$ = 41.

Do –5 < 0 nên $\left|-5\right|$ = –(–5) = 5.

Do 1,(2) > 0 nên $\left|1,\left(2\right)\right|=1,\left(2\right).$

Do $-\sqrt{5}<0$ nên $\left|-\sqrt{5}\right|=-\left(-\sqrt{5}\right)=\sqrt{5}.$

Vận dụng 4 trang 37 Toán lớp 7 Tập 1: Có bao nhiêu số thực x thỏa mãn |x| = $\sqrt{3}?$

Lời giải:

Nếu x < 0 thì $\left|x\right|$ = –x, khi đó –x = $\sqrt{3}$ do đó $x=-\sqrt{3}.$

Nếu x > 0 thì $\left|x\right|$ = x, khi đó x = $\sqrt{3}.$ 

Vậy có hai số thực x thỏa mãn $\left|x\right|=\sqrt{3}.$

Bài tập

Giải Toán 7 trang 38 Tập 1

Bài 1 trang 38 Toán lớp 7 Tập 1: Hãy thay mỗi $\boxed{?}$ bằng kí hiệu ∈ hoặc ∉ để có phát biểu đúng.

$5\boxed{?}\mathbb{Z};$                  $-2\boxed{?}\mathbb{Q};$                $\sqrt{2}\boxed{?}\mathbb{Q};$

$\frac{3}{5}\boxed{?}\mathbb{Q};$                  $2,31\left(45\right)\boxed{?}I;$        $7,62\left(38\right)\boxed{?}ℝ;$                $0\boxed{?}I.$

Lời giải:

$5\boxed{\in }\mathbb{Z};$                  $-2\boxed{\in }\mathbb{Q};$               $\sqrt{2}\boxed{\notin }\mathbb{Q};$

$\frac{3}{5}\boxed{\in }\mathbb{Q};$                 $2,31\left(45\right)\boxed{\notin }I;$       $7,62\left(38\right)\boxed{\in }ℝ;$                $0\boxed{\notin }I.$

Bài 2 trang 38 Toán lớp 7 Tập 1: Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn:

$-\frac{2}{3}$;            4,1;             $-\sqrt{2}$;         

3,2;             π;          $-\frac{3}{4}$;           $\frac{7}{3}$.

Lời giải:

Ta có: $-\frac{2}{3}=-0,\left(6\right);$  $-\sqrt{2}=-1,\mathrm{414213562...};$  $-\frac{3}{4}=-0,75;$

π = 3,141592654…; $\frac{7}{3}=2,\left(3\right).$

Do 1,414213562… > 0,75 > 0,(6) > 0 nên –1,414213562… < –0,75 < –0,(6) < 0.

hay $-\sqrt{2}<-\frac{3}{4}<-\frac{2}{3}<0.$

Do 2,(3) < 3,141592654… < 3,2 < 4,1 nên 0 < $\frac{7}{3}$ < π < 3,2 < 4,1.

Do đó $-\sqrt{2}<-\frac{3}{4}<-\frac{2}{3}<\frac{7}{3}$< π < 3,2 < 4,1.

Vậy các số theo thứ tự từ nhỏ đến lớn là: $-\sqrt{2};$  $-\frac{3}{4};$  $-\frac{2}{3};$  $\frac{7}{3};$  π;  3,2;  4,1.

Bài 3 trang 38 Toán lớp 7 Tập 1: Các khẳng định sau đúng hay sai?

a) $\sqrt{2};\sqrt{3};\sqrt{5}$ là các số thực.

b) Số nguyên không là số thực.

c) $-\frac{1}{2};\frac{2}{3};-0,45$ là các số thực.

d) Số 0 vừa là số hữu tỉ vừa là số vô tỉ.

e) 1; 2; 3; 4 là các số thực.

Lời giải:

a) Khẳng định “$\sqrt{2};\sqrt{3};\sqrt{5}$ là các số thực” là khẳng định đúng.

b) Khẳng định “Số nguyên không là số thực” là khẳng định sai.

c) Khẳng định “$-\frac{1}{2};$  $\frac{2}{3};$  –0,45 là các số thực” là khẳng định đúng.

d) Khẳng định “Số 0 vừa là số hữu tỉ vừa là số vô tỉ” là khẳng định sai.

e) Khẳng định “1; 2; 3; 4 là các số thực” là khẳng định đúng.

Bài 4 trang 38 Toán lớp 7 Tập 1: Hãy thay $\boxed{?}$ bằng các chữ số thích hợp.

a) 2,71467 > 2,7$\boxed{?}$932;

b) $-5,17934>-5,17\boxed{?}46$.

Lời giải:

a) Để 2,71467 > $2,7\boxed{?}932$ thì 1 > $\boxed{?}$ do cặp chữ số hàng phần nghìn là 4 < 9.

Vậy $\boxed{?}$ ta điền số 0.

b) Ta có –5,17934 > $-5,17\boxed{?}46$ nên 5,17934 < $5,17\boxed{?}46$

Do cặp chữ số hàng phần trăm là 7 = 7 và cặp chữ số hàng phần chục nghìn là 3 < 4 nên $9\le \boxed{?}$. Mà chỉ có số 9 thỏa mãn điều này.

Vậy $\boxed{?}$ ta điền số 9.

Bài 5 trang 38 Toán lớp 7 Tập 1: Tìm số đối của các số sau: $-\sqrt{5};$  12,(3);  0,4599;  $\sqrt{10};$  –π.

Lời giải:

Số đối của $-\sqrt{5}$ là $-\left(-\sqrt{5}\right)=\sqrt{5}.$

Số đối của 12,(3) là –12,(3).

Số đối của 0,4599 là –0,4599.

Số đối của $\sqrt{10}$ là $-\sqrt{10}$.

Số đối của –π là –(–π) = π.

Bài 6 trang 38 Toán lớp 7 Tập 1: Tìm giá trị tuyệt đối của các số sau: $-\sqrt{7};$  52,(1);  0,68;  $-\frac{3}{2};$  2π.

Lời giải:

Do $-\sqrt{7}$ < 0 nên $\left|-\sqrt{7}\right|=-\left(-\sqrt{7}\right)=\sqrt{7}.$

Do 52,(1) > 0 nên $\left|52,\left(1\right)\right|=52,1.$

Do 0,68 > 0 nên $\left|0,68\right|=0,68.$

Do $-\frac{3}{2}<0$ nên $\left|-\frac{3}{2}\right|=-\left(-\frac{3}{2}\right)=\frac{3}{2}.$

Do 2π > 0 nên $\left|2\pi \right|=2\pi .$

Bài 7 trang 38 Toán lớp 7 Tập 1: Sắp xếp theo thứ tự từ nhỏ đến lớn giá trị tuyệt đối của các số sau:

–3,2;  2,13;  $-\sqrt{2};$  $-\frac{3}{7}.$

Lời giải:

Do –3,2 < 0 nên $\left|-3,2\right|$ = –(–3,2) = 3,2.

Do 2,13 > 0 nên $\left|2,13\right|$ = 2,13.

Do $-\sqrt{2}<0$ nên $\left|-\sqrt{2}\right|=-\left(-\sqrt{2}\right)=\sqrt{2}.$

Do $-\frac{3}{7}<0$ nên $\left|-\frac{3}{7}\right|=-\left(-\frac{3}{7}\right)=\frac{3}{7}.$

Ta có: $\sqrt{2}$ = 1,414213562…; $\frac{3}{7}$ = 0,(428571);

Do 0,(428571) < 1,414213562… < 2,13 < 3,2 nên $\frac{3}{7}$ < $\sqrt{2}$ < 2,13 < 3,2.

Vậy các số theo thứ tự từ nhỏ đến lớn theo giá trị tuyệt đối là: $\frac{3}{7};\sqrt{2};2,13;3,2.$

Bài 8 trang 38 Toán lớp 7 Tập 1: Tìm giá trị của x và y biết rằng: |x| = $\sqrt{5}$ và $\left|y-2\right|=0$

Lời giải:

Xét $\left|x\right|=\sqrt{5}$

Nếu x > 0 thì $\left|x\right|$ = x, do đó x = $\sqrt{5}.$

Nếu x < 0 thì $\left|x\right|$ = –x, do đó $-x=\sqrt{5}$ hay $x=-\sqrt{5}.$

Do $\left|y-2\right|$ = 0 nên y – 2 = 0 do đó y = 2.

Vậy x = $-\sqrt{5}$ hoặc $x=\sqrt{5}$ và y = 2.

Bài 9 trang 38 Toán lớp 7 Tập 1: Tính giá trị của biểu thức: M = $\sqrt{\left|-9\right|}$

Lời giải:

Do -9 < 0 nên $\left|-9\right|$= -(-9) = 9.

Do đó $M=\sqrt{\left|-9\right|}$ = $\sqrt{9}=\sqrt{3^2}=3.$

Vậy M = 3.

Xem thêm lời giải bài tập SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 1

Bài 1: Số vô tỉ. Căn bậc hai số học

Bài 3: Làm tròn số và ước lượng kết quả

Bài 4: Hoạt động thực hành và trải nghiệm: Tính chỉ số đánh giá thể trạng BMI (Body mass index)

Bài tập cuối chương 2