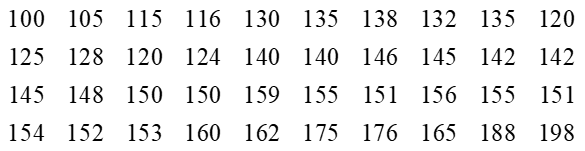Giải SGK Toán 11 (Cánh diều) Bài tập cuối chương 5

Giải Toán 11 Bài tập cuối chương 5

Bài 1 trang 25 Toán 11 Tập 2: Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm 100. Kết quả được trình bày trong Bảng 16.

Bảng 16

a) Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị:

A. 74.

B. 75.

C. 76.

D. 77.

b) Tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:

A. Q₁ ≈ 71; Q₂ ≈ 76; Q₃ ≈ 78.

B. Q₁ ≈ 71; Q₂ ≈ 75; Q₃ ≈ 78.

C. Q₁ ≈ 70; Q₂ ≈ 76; Q₃ ≈ 79.

D. Q₁ ≈ 70; Q₂ ≈ 75; Q₃ ≈ 79.

c) Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:

A. 73.

B. 74.

C. 75.

D. 76.

Lời giải:

a) Đáp án đúng là: B

Số phần tử của mẫu là: n = 40. Ta có $\frac{n}{2}=\frac{40}{2}$ = 20.

Mà 9 < 20 < 32 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.

Xét nhóm 3 là nhóm [70; 80) có r = 70, d = 10, n₃ = 23 và nhóm 2 là nhóm [60; 70) có cf₂ = 9.

Áp dụng công thức, ta có trung vị của mẫu số liệu là:

M_e = $70+\frac{20-9}{23}\cdot 10\approx 74,78$ (điểm).

Giá trị 74,78 gần nhất với giá trị 75.

b) Đáp án đúng là: D

⦁ Ta có: Q₂ = M_e ≈ 75 (điểm).

⦁ Ta có $\frac{n}{4}=\frac{40}{4}$ = 10. Mà 9 < 10 < 32 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.

Xét nhóm 3 là nhóm [70; 80) có s = 70; h = 10; n₃ = 23 và nhóm 2 là nhóm [60; 70) có cf₂ = 9.

Áp dụng công thức, ta có tứ phân vị thứ nhất là:

Q₁ = $70+\frac{10-9}{23}\cdot 10\approx 70$ (điểm).

⦁ Ta có $\frac{3n}{4}=\frac{3\cdot 40}{4}$ = 30. Mà 9 < 30 < 32 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.

Xét nhóm 3 là nhóm [70; 80) có t = 70; l = 10; n₃ = 23 và nhóm 2 là nhóm [60; 70) có cf₂ = 9.

Áp dụng công thức, ta có tứ phân vị thứ ba là:

Q₃ = $70+\frac{30-9}{23}\cdot 10\approx 79$ (điểm).

Vậy Q₁ ≈ 70; Q₂ ≈ 75; Q₃ ≈ 79.

c) Đáp án đúng là: C

Nhóm 3 là nhóm [70; 80) có tần số lớn nhất với u =  70, g = 10, n₃ = 23 và nhóm 2 có tần số n₂ = 5, nhóm 4 có tần số n₄ = 6.

Áp dụng công thức, ta có mốt của mẫu số liệu là:

M_o = $70+\frac{23-5}{2\cdot 23-5-6}\cdot 10\approx 75$ (điểm).

Bài 2 trang 25 Toán 11 Tập 2: Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác xuất để chọn được hai số có tổng là một số chẵn bằng:

A. $\frac{11}{21}$.

B. $\frac{221}{441}$.

C. $\frac{10}{21}$.

D. $\frac{1}{2}$.

Lời giải:

Đáp án đúng là: C

Ta có 21 số nguyên dương đầu tiên là: 1; 2; 3; …; 21.

− Mỗi cách chọn ra đồng thời 2 số trong 21 số khác nhau nguyên dương đầu tiên cho ta một tổ hợp chập 2 của 21 phần tử. Do đó không gian mẫu Ω gồm các tổ hợp chập 2 của 21 phần tử và $n\left(\Omega \right)=C_{21}^3$= 210.

− Xét biến cố A: “Chọn được hai số có tổng là một số chẵn”.

Trong 21 số nguyên dương đầu tiên, có 10 số chẵn và 11 số lẻ.

⦁ Trường hợp 1: Chọn được 2 số đều là số chẵn.

Có $C_{10}^2$ = 45 cách.

⦁ Trường hợp 2: Chọn được 2 số đều là số lẻ.

Có $C_{11}^2$ = 55 cách.

Như vậy, số kết quả thuận lợi cho biến cố A là n(A) = 45 + 55 = 100.

Vậy xác suất của biến cố A là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{100}{210}=\frac{10}{21}$.

Bài 3 trang 25 Toán 11 Tập 2: Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilômét) của 40 chiếc ô tô:

a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy với năm nhóm ứng với năm nửa khoảng:

[100; 120), [120; 140), [140; 160), [160; 180), [180; 200).

b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.

c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?

Lời giải:

a) Bảng tần số ghép nhóm bao gồm cả tần số tích lũy với năm nhóm ứng với năm nửa khoảng như sau:

b) ⦁ Số trung bình cộng của mẫu số liệu ghép nhóm đã cho là:

$\overline{x}=\frac{110\cdot 4+130\cdot 10+150\cdot 19+170\cdot 5+190\cdot 2}{40}$ = 145,5.

⦁ Số phần tử của mẫu là n = 40. Ta có $\frac{n}{2}=\frac{40}{2}$ = 20.

Mà 14 < 20 < 33 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.

Xét nhóm 3 là nhóm [140; 160) có r = 140, d = 20, n₃ = 19 và nhóm 2 là nhóm [120; 140) có cf₂ = 14.

Áp dụng công thức, ta có trung vị của mẫu số liệu là:

M_e = $140+\frac{20-14}{19}\cdot 20\approx 146,32$ (km).

Do đó tứ phân vị thứ hai là Q₂ = M_e ≈ 146,32 (km).

⦁ Ta có $\frac{n}{4}=\frac{40}{4}$ = 10. Mà 4 < 10 < 14 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.

Xét nhóm 2 là nhóm [120; 140) có s = 120; h = 20; n₂ = 10 và nhóm 1 là nhóm [100; 120) có cf₁ = 4.

Áp dụng công thức, ta có tứ phân vị thứ nhất là:

Q₁ = $20+\frac{10-4}{10}\cdot 20$ = 132 (km).

⦁ Ta có $\frac{3n}{4}=\frac{3\cdot 40}{4}$ = 30. Mà 14 < 30 < 33 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.

Xét nhóm 3 là nhóm [140; 160) có t = 140; l = 20; n₃ = 19 và nhóm 2 là nhóm [120; 140) có cf₂ = 14.

Áp dụng công thức, ta có tứ phân vị thứ ba là:

Q₃ = $140+\frac{30-14}{19}\cdot 20\approx 156,84$ (km).

c) Nhóm 3 là nhóm [140; 160) có tần số lớn nhất với u =  140, g = 20, n₃ = 19 và nhóm 2 có tần số n₂ = 10, nhóm 4 có tần số n₄ = 5.

Áp dụng công thức, ta có mốt của mẫu số liệu là:

M_o = $140+\frac{19-10}{2\cdot 19-10-5}\cdot 20\approx 147,83$ (km).

Bài 4 trang 26 Toán 11 Tập 2: Bạn Dũng và bạn Hương tham gia đội văn nghệ của nhà trường. Nhà trường chọn từ đội văn nghệ đó một bạn nam và một bạn nữ để lập tiết mục song ca. Xác suất được nhà trường chọn vào tiết mục song ca của Dũng và Hương lần lượt là 0,7 và 0,9.

Tính xác suất của các biến cố sau:

a) A: “Cả hai bạn được chọn vào tiết mục song ca”;

b) B: “Có ít nhất một bạn được chọn vào tiết mục song ca”;

c) C: “Chỉ có bạn Hương được chọn vào tiết mục song ca”.

Lời giải:

Xét hai biến cố:

D: “Bạn Dũng được chọn vào tiết mục song ca”.

E: “Bạn Hương được chọn vào tiết mục song ca”.

Từ giả thiết suy ra D, E là hai biến cố độc lập và P(D) = 0,7; P(E) = 0,9.

a) Do A = D ∩ E nên P(A) = P(D ∩ E) = P(D) . P(E) = 0,7 . 0,9 = 0,63.

b) Do B = D ∪ E nên ta có:

P(B) = P(D ∪ E) = P(D) + P(E) – P(D ∩ E) = 0,7 + 0,9 – 0,63 = 0,97.

c) Xét biến cố đối của biến cố D là $\overline{D}$: “Bạn Dũng không được chọn vào tiết mục song ca”. Do đó $P\left(\overline{D}\right)=1-P\left(D\right)$ = 1 - 0,7 = 0,3 và E, $\overline{D}$ là hai biến cố độc lập.

Do C = $E\cap \overline{D}$ nên P(C) = $P\left(E\cap \overline{D}\right)=P\left(E\right)\cdot P\left(\overline{D}\right)$ = 0,9 - 0,3 = 0,27.

Bài 5 trang 26 Toán 11 Tập 2: Hai bạn Mai và Thi cùng tham gia một kì kiểm tra ngoại ngữ một cách độc lập nhau. Xác suất để bạn Mai và bạn Thi đạt từ điểm 7 trở lên lần lượt là 0,8 và 0,9. Tính xác suất của biến cố C: “Cả hai bạn đều đạt từ điểm 7 trở lên”.

Lời giải:

Xét hai biến cố:

A: “Bạn Mai đạt từ điểm 7 trở lên”;

B: “Bạn Thi đạt từ điểm 7 trở lên”.

Từ giả thiết ta suy ra A, B là hai biến cố độc lập và P(A) = 0,8; P(B) = 0,9.

Do C = A ∩ B nên P(C) = P(A) . P(B) = 0,8 . 0,9 = 0,72.

Bài 6 trang 26 Toán 11 Tập 2: Một người chọn ngẫu nhiên 3 lá thư vào 3 phong bì đã ghi địa chỉ sao cho mỗi phong bì chỉ chứa một lá thư. Tính xác suất để có ít nhất một lá thư được cho vào đúng phong bì đã ghi địa chỉ theo lá thư đó.

Lời giải:

Không gian mẫu của phép thử trên có 3! = 6 phần tử, tức là n(Ω) = 6.

Xét A là biến cố “Có ít nhất một lá thư được cho vào đúng phong bì”.

Biến cố đối của biến cố A là $\overline{A}$: “Không có lá thư nào được bỏ đúng phong bì” và $n\left(\overline{A}\right)$ = 2! = 2.

Suy ra $P\left(\overline{A}\right)=\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{2}{6}=\frac{1}{3}$.

Do đó P(A) = $1-P\left(\overline{A}\right)=1-\frac{1}{3}=\frac{2}{3}$.

Bài 7 trang 26 Toán 11 Tập 2: Một hộp chứa 9 quả cầu có cùng kích thước và khối lượng. Trong đó có 4 quả cầu màu xanh đánh số từ 1 đến 4, có 3 quả cầu màu vàng đánh số từ 1 đến 3, có 2 quả cầu màu đỏ đánh số từ 1 đến 2. Lấy ngẫu nhiên 2 quả cầu từ hộp. Tính xác suất để 2 quả cầu được lấy vừa khác màu vừa khác số.

Lời giải:

− Mỗi cách chọn ra đồng thởi 2 quả cầu từ hộp chứa 9 quả cầu cho ta một tổ hợp chập 2 của 9 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 2 của 9 phần tử và $n\left(\Omega \right)=C_9^2$ = 36.

− Xét biến cố A: “Chọn được 2 quả cầu vừa khác màu vừa khác số”.

+ Chọn 2 quả cầu khác màu:

⦁ 1 quả màu xanh và 1 quả màu vàng có $C_4^1\cdot C_3^1$ = 12 cách chọn;

⦁ 1 quả màu xanh và 1 quả màu đỏ có $C_4^1\cdot C_2^1$ = 8 cách chọn;

⦁ 1 quả màu vàng và 1 quả màu đỏ có $C_3^1\cdot C_2^1$ = 6 cách chọn.

Do đó số cách chọn 2 quả cầu khác màu là: 12 + 8 + 6 = 26 cách chọn.

+ Trong 26 cách chọn 2 quả cầu khác màu trên thì sẽ có 2 trường hợp đối với 2 quả cầu đó là khác số  hoặc cùng số.

Xét các trường hợp 2 quả cầu khác màu cùng số:

⦁ 2 quả cầu cùng số 1: $C_3^2$ = 3 cách chọn;

⦁ 2 quả cầu cùng số 2: $C_3^2$ = 3 cách chọn;

⦁ 2 quả cầu cùng số 3: $C_2^2$ = 3 cách chọn.

Do đó số cách lấy ra 2 quả cầu khác màu cùng số là 3 + 3 + 1 = 7 cách.

Suy ra số cách lấy ra 2 quả cầu khác màu khác số là 26 – 7 = 19 cách, tức là n(A) = 19.

Vậy xác suất để lấy ra 2 quả cầu khác màu khác số là P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{19}{36}$.

Bài 8 trang 26 Toán 11 Tập 2: Để nghiên cứu xác suất của một loại cây trồng mới phát triển bình thường, người ta trồng hạt giống của loại cây đó trên hai lô đất thí nghiệm A, B khác nhau. Xác suất phát triển bình thường của hạt giống đó trên các lô đất A, B lần lượt là 0,7 và 0,6. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng, tính xác suất hạt giống chỉ phát triển bình thường trên một lô đất.

Lời giải:

− Xét các biến cố:

A: “Hạt giống phát triển bình thường trên lô đất thí nghiệm A”;

B: “Hạt giống phát triển bình thường trên lô đất thí nghiệm B”;

Từ giả thiết ta thấy A, B là hai biến cố độc lập và P(A) = 0,7; P(B) = 0,6.

Xét các biến cố đối:

$\overline{A}$: “Hạt giống không phát triển bình thường trên lô đất thí nghiệm A”;

$\overline{B}$: “Hạt giống không phát triển bình thường trên lô đất thí nghiệm B”.

Ta có $P\left(\overline{A}\right)$ = 1 - P(A) = 1 - 0,7 = 0,3; $P\left(\overline{B}\right)$ = 1 - P(B) = 1 - 0,6 = 0,4.

− Xét các biến cố:

H: “Hạt giống chỉ phát triển bình thường trên một lô đất”.

H₁: “Hạt giống phát triển bình thường trên lô đất A và không phát triển bình thường trên lô đất B”

H₂: “Hạt giống phát triển bình thường trên lô đất B và không phát triển bình thường trên lô đất A”

⦁ Ta thấy A, $\overline{B}$ là hai biến cố độc lập và H₁ = $A\cap \overline{B}$

Nên $P\left(H_1\right)=P\left(A\cap \overline{B}\right)=P\left(A\right)\cdot P\left(\overline{B}\right)$ = 0,7.0,4 = 0,28.

⦁ Ta thấy B, $\overline{A}$ là hai biến cố độc lập và H₁ = $B\cap \overline{A}$

Nên $P\left(H_2\right)=P\left(B\cap \overline{A}\right)=P\left(B\right)\cdot P\left(\overline{A}\right)$ = 0,6.0,3 = 0,18.

⦁ Ta thấy H = H₁ ∪ H₂, mà H₁, H₂ là hai biến cố xung khắc

Nên P(H) = P(H₁ ∪ H₂) = P(H₁) + P(H₂) = 0,28 + 0,18 = 0,46.

Vậy xác suất hạt giống chỉ phát triển bình thường trên một lô đất bằng 0,46.

Chú ý: Ta có thể tính xác suất theo biến cố đối của biến cố H.

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: