Giải SBT Toán 8 (Chân trời sáng tạo) Bài 2: Các phép toán với đa thức nhiều biến

Giải SBT Toán 8 Bài 2: Các phép toán với đa thức nhiều biến

Bài 1 trang 10 SBT Toán 8: Tính:

a) 7x + (–3xy + 5x);

b) 4x – 3y – (3 + 3x – y);

c) 2xy – 4xy – (y – 3xy);

d) (x2y – 3xy2 – y2) + (5xy2 – 4y2 + 5x2y).

Lời giải:

a) 7x + (–3xy + 5x)

= 7x ‒ 3xy + 5x

= (7x + 5x) ‒ 3xy

= 12x ‒ 3xy.

b) 4x – 3y – (3 + 3x – y)

= 4x – 3y – 3 ‒ 3x + y

= (4x ‒ 3x) + (– 3y + y) – 3

= x ‒ 2y ‒ 3.

c) 2xy – 4xy – (y – 3xy)

= 2xy – 4xy – y + 3xy

= (2xy – 4xy + 3xy) – y

= xy ‒ y.

d) (x²y – 3xy² – y²) + (5xy² – 4y² + 5x²y)

= x²y – 3xy² – y² + 5xy² – 4y² + 5x²y

= (x²y + 5x²y) + (– 3xy² + 5xy²) +(– y² – 4y²)

= 6x²y + 2xy² – 5y².

Bài 2 trang 10 SBT Toán 8: Tính:

a) 2a + 4b + (–4b + 5a) – (6a – 9b);

b) 6а – [b + 3а – (4a – b)].

Lời giải:

a) 2a + 4b + (–4b + 5a) – (6a – 9b)

= 2a + 4b – 4b + 5a – 6a + 9b

= (2a + 5a ‒ 6a) + (4b – 4b + 9b)

= a + 9b.

b) 6а – [b + 3а – (4a – b)]

= 6a – [b + 3a – 4a + b]

= 6a – [2b – a]

= 6a – 2b + a

= 7a ‒ 2b.

Bài 3 trang 10 SBT Toán 8: Thực hiện các phép nhân:

Bài 4 trang 10 SBT Toán 8: Thực hiện các phép nhân:

a) (x + 3y)(x – 2y);

b) (2x – y)(y – 5x);

c) (2x – 5y)(y² – 2xy);

d) (x – y)(x² – xy – y²).

Lời giải:

a) (x + 3y)(x – 2y)

= x.x + x.(‒2y) + 3y.x + 3y.(‒2y)

= x² ‒ 2xy + 3xy ‒ 6y²

= x² + (‒2xy + 3xy) ‒ 6y²

= x² + xy ‒ 6y².

b) (2x – y)(y – 5x)

= 2x.y + 2x.(‒5x) ‒ y.y + (‒y).(‒5x)

= 2xy ‒ 10x² ‒ y² + 5xy

= (2xy + 5xy) ‒ 10x² ‒ y²

= 7xy ‒ 10x² ‒ y².

c) (2x – 5y)(y² – 2xy)

= 2x.y² + 2x.(‒2xy) + (‒5y).y² + (‒5y).(‒2xy)

= 2xy² ‒ 4x²y ‒ 5y³ + 10xy²

= (2xy² + 10xy²) ‒ 4x²y ‒ 5y³

= 12xy² ‒ 4x²y ‒ 5y³.

d) (x – y)(x² – xy – y²)

= x.x² + x.(‒xy) + x.(‒y²) + (‒y).x² + (‒y).(‒xy) + (‒y).(‒y²)

= x³ ‒ x²y ‒ xy² ‒ x²y + xy² + y³

= x³ + (‒ x²y ‒ x²y) +(‒ xy² + xy²) + y³

= x³ ‒ 2x²y + y³.

Bài 5 trang 10 SBT Toán 8: Thực hiện các phép chia:

a) 24xy³ : (6xy);

b) ‒3x²y⁵z : (15xy³);

c) (‒4x⁶y²) : (‒0,1x³y²).

Lời giải:

a) 24xy³ : (6xy) = (24 : 6).(x : x).(y³ : y) = 4y².

b) ‒3x²y⁵z : (15xy³) = (‒3 : 15).(x² : x).(y⁵ : y³).z 

c) (‒4x⁶y²) : (‒0,1x³y²) = [(‒4 : (‒0,1)].(x⁶ : x³).(y² : y²) = 40x^3.

Bài 6 trang 10 SBT Toán 8: Thực hiện các phép chia:

a) (6x²y ‒ 9xy²) : (3xy);

b) (‒xy² +10y) : (‒5y);

c) $\left(5x{y}^2+2\right):\frac{5}{2};$

d) (2x⁴y² – 3x²y³) : (–x²y).

Lời giải:

a) (6x²y ‒ 9xy²) : (3xy)

= 6x²y : 3xy ‒ 9xy² : 3xy

= (6 : 3).(x² : x).(y : y) ‒ (9 : 3).(x : x).(y² : y)

= 2x ‒ 3y.

b) (‒xy² +10y) : (‒5y)

= ‒xy² : (‒5y) + 10y : (‒5y)

= [(‒1) : (‒5)]x.(y² : y) + [10 : (‒5)].(y : y)

$=\frac{1}{5}xy-2.$

c) $\left(5x{y}^2+2\right):\frac{5}{2}$

$=5x{y}^2:\frac{5}{2}+2:\frac{5}{2}$

$=\left(5:\frac{5}{2}\right)x{y}^2+\frac{4}{5}$

$=2x{y}^2+\frac{4}{5}.$

d) (2x⁴y² – 3x²y³) : (–x²y)

= 2x⁴y² : (–x²y) – 3x²y³ : (–x²y)

= [2 : (‒1)].(x⁴ : x²).(y² : y) ‒ [3 : (‒1)].(x² : x²).(y³ : y)

= ‒2x²y + 3y².

Bài 7 trang 10 SBT Toán 8: Tính:

a) 3a(a – b) – b(b – 3a);

b) 3a²(2a + b) – 2b(4a² – b);

c) (a + b)(a – b)(a – 1)(a – 2);

d) b(3b² – a³) + (a² + 3b)(ab – b²).

Lời giải:

a) 3a(a – b) – b(b – 3a)

= 3a² ‒ 3ab ‒ b² + 3ab

= 3a² + (‒3ab + 3ab) ‒ b²

= 3a² ‒ b².

b) 3a²(2a + b) – 2b(4a² – b)

= 6a³ + 3a²b ‒ 8a²b + 2b²

= 6a³ + (3a²b ‒ 8a²b) + 2b²

= 6a³ ‒ 5a²b + 2b².

c) (a + b)(a – b) ‒ (a – 1)(a – 2)

= (a² ‒ ab + ab ‒ b²) ‒ (a² ‒ 2a ‒ a + 2)

= (a² ‒ b²) ‒ (a² ‒ 3a + 2)

= a² ‒ b² ‒ a² + 3a ‒ 2

= (a² ‒ a²) ‒ b² + 3a ‒ 2

= ‒ b² + 3a ‒ 2.

d) b(3b² – a³) + (a² + 3b)(ab – b²).

= 3b³ ‒ a³b + a³b ‒ a²b² + 3ab² ‒ 3b³

= (3b³ ‒ 3b³) + (‒a³b + a³b) ‒ a²b² + 3ab²

= ‒ a²b² + 3ab².

Bài 8 trang 10 SBT Toán 8: Tính giá trị của đa thức:

a) (3x − y) + (3y − x) − (x + y) tại x = 2,7 và y = 1,3;

b) x(x + y) − y(x − y) tại x = –0,5 và y = 0,3;

c) (1,3x²y + 3,2xy + 1,5y²) – (2,2xy − 1,2x²y + 1,5y²) tại x = −2 và y = 5.

Lời giải:

a) (3x − y) + (3y − x) − (x + y)

= 3x − y + 3y − x − x ‒ y

= (3x ‒ x ‒ x) + (‒y + 3y ‒ y)

= x + y.

Với x = 2,7 và y = 1,3 ta có: 2,7 + 1,3 = 4.

b) x(x + y) − y(x − y)

= x² + xy ‒ xy + y²

= x² + (xy ‒ xy) + y² = x² + y².

Với x = –0,5 và y = 0,3 ta có:

(–0,5)² + 0,3² = 0,25 + 0,09 = 0,34.

c) (1,3x²y + 3,2xy + 1,5y²) – (2,2xy − 1,2x²y + 1,5y²)

= 1,3x²y + 3,2xy + 1,5y² – 2,2xy + 1,2x²y ‒ 1,5y²

= (1,3x²y + 1,2x²y) + (3,2xy – 2,2xy) + (1,5y² ‒ 1,5y²)

= 2,5x²y + xy.

Với x = −2 và y = 5 ta có:

2,5.(‒2)².5 + (‒2).5 = 50 ‒ 10 = 40.

Bài 9 trang 10 SBT Toán 8: Biết rằng x = a + b và y = 2a – b. Tính các đa thức sau theo a và b.

a) A = 3x – 4y;

b) B = 2xy.

Lời giải:

a) A = 3(a + b) ‒ 4(2a ‒ b)

= 3a + 3b ‒ 8a + 4b

= (3a ‒ 8a) + (3b + 4b)

= ‒5a + 7b.

b) B = 2(a + b)(2a ‒ b)

= 2(2a² ‒ ab + 2ab ‒ b²)

= 2(2a² + ab ‒ b²)

= 4a² + 2ab ‒ 2b².

Bài 10 trang 11 SBT Toán 8: Từ một tấm tôn hình chữ nhật có chiều dài bằng a (cm), chiều rộng bằng b (cm), người ta cắt bỏ bốn hình vuông cạnh bằng x (cm) ở bốn góc, rồi gấp và hàn thành thùng không có nắp (Hình 1). Viết biểu thức biểu thị:

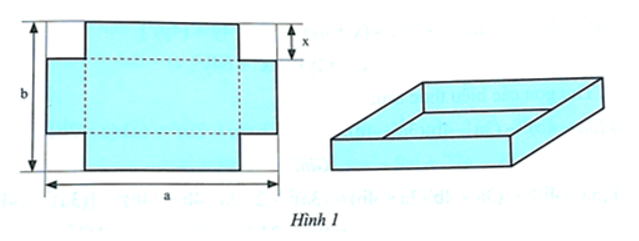
a) Thể tích nước tối đa mà thùng có thể chứa được.

b) Tổng diện tích của năm mặt của chiếc thùng.

Lời giải:

a) Thể tích nước tối đa mà thùng có thể chứa được là:

V = (a ‒ 2x)(b ‒ 2x)x = (ab – 2ax – 2bx + 4x²)x

= abx ‒ 2ax² ‒ 2bx² + 4x³ (cm³).

b) Tổng diện tích của năm mặt của chiếc thùng bằng diện tích hình chữ nhật trừ đi tổng diện tích bốn hình vuông cạnh bằng x ở 4 góc.

Vậy S = ab ‒ 4x² (cm²).

Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Đơn thức và đa thức nhiều biến

Bài 3: Hằng đẳng thức đáng nhớ

Bài 4: Phân tích đa thức thành nhân tử

Bài 5: Phân thức đại số

Bài 6: Cộng, trừ phân thức