Giải SBT Toán 7 (Cánh diều) Bài 5: Biểu diễn thập phân của số hữu tỉ

Giải Sách bài tập Toán lớp 7 Bài 5: Biểu diễn thập phân của số hữu tỉ

Giải SBT Toán 7 trang 24 Tập 1

Bài 39 trang 24 SBT Toán 7 Tập 1: Chọn cụm từ "số hữu tỉ", "số thập phân hữu hạn", "số thập phân vô hạn tuần hoàn" thích hợp cho $\boxed{?}$:

a) Mỗi $\boxed{?}$ được biểu diễn một $\boxed{?}$ hoặc vô hạn tuần hoàn;

b) Số hữu tỉ $\frac{17}{18}$ viết được dưới dạng $\boxed{?}$;

c) Kết quả của phép tính $\frac{233}{2^2.5^2}$ viết được dưới dạng $\boxed{?}$.

Lời giải:

a) Mỗi số hữu tỉ được biểu diễn một số thập phân hữu hạn hoặc vô hạn tuần hoàn;

b) Ta có: $\frac{17}{18}=0,9\left(4\right)$.

Vì số 0,9(4) là số thập phân vô hạn tuần hoàn nên:

Số hữu tỉ $\frac{17}{18}$ viết được dưới dạng số thập phân vô hạn tuần hoàn;

c) Ta có: $\frac{233}{2^2.5^2}=\frac{233}{4.25}=\frac{233}{100}=2,33$.

Vì số 2,33 là số thập phân hữu hạn nên:

Kết quả của phép tính $\frac{233}{2^2.5^2}$ viết được dưới dạng số thập phân hữu hạn.

Bài 40 trang 24 SBT Toán 7 Tập 1: Viết mỗi số hữu tỉ sau dưới dạng số thập phân hữu hạn:

$\frac{33}{8};\frac{543}{125};\frac{-11247}{500}$.

Lời giải:

Ta có:

$$\begin{gathered} \frac{33}{8}=4,125;\frac{543}{125}=4,344; \\ \frac{-11247}{500}=-2,494 \end{gathered}$$

Vậy các số hữu tỉ $\frac{33}{8};\frac{543}{125};\frac{-11247}{500}$ viết dưới dạng số thập phân hữu hạn lần lượt là 4,125; 4,344; −2,494.

Bài 41 trang 24 SBT Toán 7 Tập 1: Viết mỗi số hữu tỉ sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để nhận rõ chu kỳ):

$\frac{13}{24};\frac{-35}{111};\frac{-77}{1350}$.

Lời giải:

Ta có:

$$\begin{gathered} \frac{13}{24}=0,541\left(6\right);\frac{-35}{111}=-0,\left(315\right); \\ \frac{-77}{1350}=-0,05\left(703\right) \end{gathered}$$

Vậy các số hữu tỉ $\frac{13}{24};\frac{-35}{111};\frac{-77}{1350}$ viết dưới dạng số thập phân vô hạn tuần hoàn lần lượt là 0,541(6); −0,(315); −0,05(703).

Bài 42 trang 24 SBT Toán 7 Tập 1: Viết mỗi số hữu tỉ sau dưới dạng phân số tối giản:

0,12; 0,136; −7,2625.

Lời giải:

Ta có:

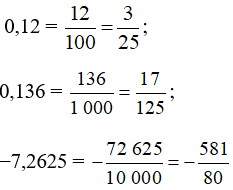
Vậy các số hữu tỉ 0,12; 0,136; −7,2625 viết dưới dạng số thập phân vô hạn tuần hoàn lần lượt là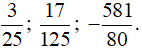 

Bài 43 trang 24 SBT Toán 7 Tập 1: Viết thương mỗi phép chia sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để nhận rõ chu kỳ):

a) 1 : 11;

b) 17 : 333;

c) 4,3 : 99;

d) 18,7 : 6,6.

Lời giải:

Thực hiện phép chia, ta được:

a) 1 : 11 = 0,(09);

b) 17 : 333 = 0,(051);

c) 4,3 : 99 = 0,0(43);

d) 18,7 : 6,6 = 2,8(3).

Bài 44 trang 24 SBT Toán 7 Tập 1: Chữ số thập phân thứ 221 sau dấu "," của số hữu tỉ $\frac{1}{7}$ được viết dưới dạng số thập phân vô hạn tuần hoàn là chữ số nào?

Lời giải:

Ta có: $\frac{1}{7}=0,\left(142857\right)$ là số thập phân vô hạn tuần hoàn với chu kì gồm 6 chữ số.

Mặt khác, ta lại có: 221 = 6 . 36 + 5.

Do đó, chữ số thập phân thứ 221 sau dấu "," của số hữu tỉ $\frac{1}{7}$ được viết dưới dạng số thập phân vô hạn tuần hoàn là chữ số thứ năm trong chu kì.

Vậy chữ số cần tìm là 5.

Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

Bài 4: Thứ tự thực hiện phép tính. Quy tắc dấu ngoặc

Bài tập cuối chương 1

Bài 1: Số vô tỉ. Căn bậc hai số học

Bài 2: Tập hợp ℝ các số thực