Sách bài tập Toán 6 Bài 9: Dấu hiệu chia hết
Lời giải:
Số chia hết cho 2 là số có chữ số tận cùng là 0; 2; 4; 6; 8
Do đó các số chia hết cho 2 trong các số đã cho là: 2 020; 2 022; 3 306
+) 2 020 có tổng các chữ số là 2 + 0 + 2 + 0 = 4, vì 4 ⋮̸ 3 nên 2 020 ⋮̸ 3
+) 2 022 có tổng các chữ số là 2 + 0 + 2 + 2 = 6, vì 6 ⁝ 3 nên 2 022 ⁝ 3
+) 3 306 có tổng các chữ số là 3 + 3 + 0 + 6 = 12, vì 12 ⁝ 3 nên 3 306 ⁝ 3
Vậy các số chia hết cho cả 2 và 3 là: 2 020; 3 306.
Lời giải:
Số chia hết cho 5 là số có chữ số tận cùng là 0 hoặc 5.
Do đó các số chia hết cho 5 trong các số trên là: 1 010; 1 945; 2 010.
+) 1 010 có tổng các chữ số là 1 + 0 + 1 + 0 = 2, vì 2 ⋮̸ 3 nên 1 010 ⋮̸ 3
+) 1 945 có tổng các chữ số là 1 + 9 + 4 + 5 = 19, vì 19 ⋮̸ 3 nên 1 945 ⋮̸ 3
+) 2 010 có tổng các chữ số là 2 + 0 + 1 + 0 = 3, vì 3 ⁝ 3 nên 2 010 ⁝ 3
Vậy số chia hết cho cả 3 và 5 là: 2 010
Lời giải:
Trong các số trên, các số 2 340; 2 010; 2 020 đều có chữ số tận cùng là 0
Do đó 2 340; 2 010; 2 020 đều chia hết cho 2
+) 2 340 có tổng các chữ số là 2 + 3 + 4 + 0 = 9, vì 9 ⁝ 9 nên 2 340 ⁝ 9
+) 2 010 có tổng các chữ số là 2 + 0 + 1 + 0 = 3, vì 3 ⋮̸ 9 nên 2 010 ⋮̸ 9
+) 2 020 có tổng các chữ số là 2 + 0 + 2 + 0 = 4, vì 4 ⋮̸ 9 nên 2 020 ⋮̸ 9
Vậy số chia hết cho cả 2 và 9 là: 2 340.
a) 2 020 + 2 022; b) 20213 – 20203
Lời giải:
a) Vì 2 020 ⁝ 2 (do 2 020 có chữ số tận cùng là 0)
2 022 ⁝ 2 (do 2 022 có chữ số tận cùng là 2)
Do đó (2 020 + 2 022) ⁝ 2 (áp dụng tính chất chia hết của một tổng)
Vậy 2 020 + 2 022 chia hết cho 2
b) Vì 2 021 là số lẻ 20203 là số lẻ nên 20213 ⋮̸ 2
2 020 ⁝ 2 nên 20203 ⁝ 2
Do đó ( 20213 – 20203 ) ⋮̸ 2(áp dụng tính chất chia hết của một hiệu)
Vậy ( 20213 – 20203 ) không chia hết cho 2.
a) 2 020 + 2 021; b) 20255 – 20204
Lời giải:
a) Vì 2 020 ⁝ 5 (do 2 020 có chữ số tận cùng là 0)
2 021 ⋮̸ 5 (do 2 020 có chữ số tận cùng là 1)
Do đó (2 020 + 2 021) ⋮̸ 5 (áp dụng tính chất chia hết của một tổng)
Vậy (2 020 + 2 021) không chia hết cho 5.
b) Vì 2 025 ⁝ 5 nên 20255 ⁝ 5
2 020 ⁝ 5 nên 20204 ⁝ 5
Do đó (20255 – 20204)⁝ 5 (áp dụng tính chất chia hết của một hiệu)
Vậy (20255 – 20204) chia hết cho 5.
Lời giải:
Vì khi biểu diễn có thể tách ra đều thành từng nhóm 3 người hoặc 5 người nên số người của nhóm nhảy phải chia hết cho cả 3 và 5.
Số tự nhiên nhỏ nhất chia hết cho cả 3 và 5 khác 0 là 15
Vậy nhóm nhảy cần ít nhất 15 người.
c) Các số đó chia hết cho cả 2 và 5.
Lời giải:
Gọi số có bốn chữ số cần tìm là 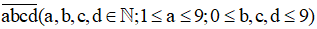 và
và
Vì để tạo ra các số có bốn chữ số thỏa mãn yêu cầu đề bài nên a, b, c, d ∈ { 0; 2; 3; 5}
Vì mỗi chữ số đã cho chỉ lấy 1 lần từ 4 chữ số 0; 2; 3; 5 nên 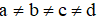
a) Để số đó chia hết cho 2 nên số đó có chữ số tận cùng là 0; 2; 4; 6; 8.
Do đó d = 0 hoặc d = 2
+) Với d = 0, ta được các số: 5 320; 5 230; 3 520; 3 250; 2 530; 2 350.
+) Với d = 2, a khác 0 ta được các số: 5 302; 5 032; 3 502; 3 052
Vậy các số chia hết cho 2 là 5 320; 5 230; 3 520; 3 250; 2 530; 2 350; 5 302; 5 032;
3 502; 3 052.
b) Để số đó chia hết cho 5 nên số đó có chữ số tận cùng là 0 hoặc 5.
Do đó d = 0 hoặc d = 5
+) Với d = 0, ta được các số: 3 520; 3 250; 2 530; 2 350; 5 320; 5 230
+) Với d = 5, a khác 0 ta được các số: 3 025; 3 205; 2 035; 2 305.
Vậy các số chia hết cho 5 là: 3 520; 3 250; 2 530; 2 350; 5 320; 5 230; 3 025; 3 205; 2 035; 2 305.
c) Để số đó chia hết cho cả 2 và 5 nên số đó phải có chữ số tận cùng là 0. Do đó d = 0
Với d = 0 ta được các số: 3 520; 3 250; 2 530; 2 350; 5 320; 5 230
Vậy các số chia hết cho cả 2 và 5 là 3 520; 3 250; 2 530; 2 350; 5 320; 5 230.
Lời giải:
Vì n chia hết cho 5 nên n có chữ số tận cùng là 0 hoặc 5. Do đó b = 0 hoặc b = 5
+) Với b = 0 ta được số 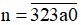
Để n chia hết cho 9 thì (3 + 2 + 3 + a + 0) chia hết cho 9 hay (8 + a) chia hết cho 9.
Mà 0 ≤ a ≤ 9 nên a = 1. Ta được số cần tìm là 32 310.
+) Với b = 5 ta được số 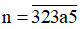
Để n chia hết cho 9 thì (3 + 2 + 3 + a + 5) chia hết cho 9 hay (13 + a) chia hết cho 9.
Mà 0 ≤ a ≤ 9 nên a = 5. Ta được số cần tìm là 32 355.
Vậy cặp số (a; b) thỏa mãn là (1; 0); (5; 5).
Lời giải:
Gọi số bút mẹ mua cho Mai là x (cái, x ∈ N*)
số vở mẹ mua cho Mai và y (quyển, y ∈ N*)
Mẹ Mai mua bút hết số tiền là:
17. x (nghìn đồng)
Mẹ Mai mua vở hết số tiền là:
5.y (nghìn đồng)
Vì mẹ Mai mua hết tất cả 165 nghìn đồng nên ta có: 17. x + 5. y = 165
17. x = 165 – 5.y
Vì 165 ⁝ 5; 5y ⁝ 5( do 5 ⁝ 5) nên (165 – 5y) ⁝ 5. Vì thế (17x) ⁝ 5
Vì mẹ Mai mua hết 165 nghìn đồng nên 17. x < 165
Ta có bảng sau:
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
17. x |
17 |
34 |
51 |
68 |
85 |
102 |
119 |
136 |
153 |
170 |
Vì (17x) ⁝ 5 nên x = 5 (vì 85 chia hết cho 5). Suy ra 17. 5 = 165 – 5. y
165 - 5. y = 85
5. y = 165 – 85
5. y = 80
y = 80: 5
y = 16
Vậy mẹ mua cho Mai 5 cái bút và 16 quyển vở.
Bài 2.21 trang 34 sách bài tập Toán lớp 6 Tập 1: Tổng sau có chia hết cho 3 hay không? Vì sao?
Lời giải:
a) A = 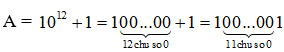
Ta có 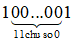 có tổng các chữ số là (1 + 0 + 0 + … + 0 + 1) = 2
có tổng các chữ số là (1 + 0 + 0 + … + 0 + 1) = 2
Vì 2 ⋮̸ 3 nên 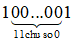 ⋮̸ 3 hay A⋮̸ 3
⋮̸ 3 hay A⋮̸ 3
Vậy A không chia hết cho 3.
b) B = 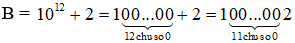
Ta có 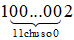 có tổng các chữ số là (1 + 0 + 0 + … + 0 + 2) = 3
có tổng các chữ số là (1 + 0 + 0 + … + 0 + 2) = 3
Vì 3 ⁝ 3 nên 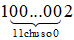 ⁝ 3 hay B ⁝ 3
⁝ 3 hay B ⁝ 3
Vậy B chia hết cho 3.
Bài 2.22 trang 34 sách bài tập Toán lớp 6 Tập 1: Tổng sau có chia hết cho 9 hay không? Vì sao?
Lời giải:
a) A = 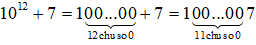
Ta có 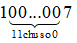 có tổng các chữ số là (1 + 0 + 0 + … + 0 + 7) = 8
có tổng các chữ số là (1 + 0 + 0 + … + 0 + 7) = 8
Vì 8 ⋮̸ 9 nên 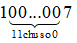 ⋮̸ 9 hay A ⋮̸ 9
⋮̸ 9 hay A ⋮̸ 9
Vậy A không chia hết cho 9.
b) B = 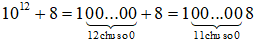
Ta có 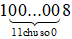 có tổng các chữ số là (1 + 0 + 0 + … + 0 + 8) = 9
có tổng các chữ số là (1 + 0 + 0 + … + 0 + 8) = 9
Vì 9 ⁝ 9 nên 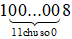 ⁝ 9 hay B ⁝ 9
⁝ 9 hay B ⁝ 9
Vậy B chia hết cho 9.
Xem thêm các bài giải SBT Toán 6 Kết nối tri thức hay, chi tiết khác:
Bài 8: Quan hệ chia hết và tính chất


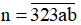 . Hãy thay a, b bởi các chữ số thích hợp, biết n vừa chia hết cho 5, vừa chia hết cho 9.
. Hãy thay a, b bởi các chữ số thích hợp, biết n vừa chia hết cho 5, vừa chia hết cho 9.