Sách bài tập Toán 6 Bài 11: Ước chung. Ước chung lớn nhất
Bài 2.33 trang 39 sách bài tập Toán lớp 6 Tập 1: Hãy tìm tập hợp Ư(105), Ư(140) và ƯC(105, 140).
Lời giải:
+) Phân tích 105 ra thừa số nguyên tố: 105 = 3. 5. 7
Vì 105 chia hết cho các số: 1; 3; 5; 7; 15; 21; 35; 105
Do đó: Ư(105) = {1; 3; 5; 7; 15; 21; 35; 105}
+) Phân tích 140 ra thừa số nguyên tố: 105 = . 5. 7
Vì 140 chia hết cho các số: 1; 2; 4; 5; 7; 10; 14; 20; 28; 35; 70; 140
Do đó: Ư(140) = {1; 2; 4; 5; 7; 10; 14; 20; 28; 35; 70; 140}.
Khi đó ƯC(105, 140) = {1; 5; 7; 35}.
Bài 2.34 trang 39 sách bài tập Toán lớp 6 Tập 1: Tìm ƯCLN của:
Lời giải:
a) Vì 105 35 nên ƯCLN(35, 105) = 35.
Vậy ƯCLN(35, 105) = 35.
b) Vì 180 15; 165 15 nên ƯCLN(15, 180, 165) = 15.
Vậy ƯCLN(15, 180, 165) = 15.
Lời giải:
a)
Phân tích các số 72 và 90 ra thừa số nguyên tố:
72 = 23.32; 90 = 2.32.5;
+) Ta chọn ra các thừa số nguyên tố chung là: 2 và 3.
+) Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 3 là 2. Khi đó:
ƯCLN(72; 90) = 2. 32 = 18. Ta được ƯC(72; 90) = Ư(18) = {1; 2; 3; 6; 9; 18}
Vậy ƯCLN(72; 90) = 18 và ƯC(72; 90) = {1; 2; 3; 6; 9; 18}.
b) Phân tích các số 200; 245 và 125 ra thừa số nguyên tố:
;200 = 23.52 245 = 5.72 125 = 53
+) Ta chọn ra thừa số nguyên tố chung là: 5.
+) Số mũ nhỏ nhất của 5 là 1
ƯCLN(200; 245; 125) = 5. Ta được ƯC(200; 245; 125) = Ư(5) = {1; 5}
Vậy ƯCLN(200; 245; 125) = 5 và ƯC(200; 245; 125) = {1; 5}.
Bài 2.36 trang 39 sách bài tập Toán lớp 6 Tập 1: Điền các từ thích hợp vào chỗ chấm:
a) Nếu a ⁝ 7 và b ⁝ 7 thì 7 là……. của a và b.
b) Nếu 9 là số lớn nhất sao cho a ⁝ 9 và b ⁝ 9 thì 9 là …….. của a và b.
Lời giải:
a) Nếu a ⁝ 7 và b ⁝ 7 thì 7 là ước chung của a và b.
b) Nếu 9 là số lớn nhất sao cho a ⁝ 9 và b ⁝ 9 thì 9 là ước chung lớn nhất của a và b.
Lời giải:
Gọi x là số chiếc bút trong mỗi hộp bút chì màu (chiếc, x ∈ N*; x > 2)
Theo bài ra ta có: 25 chia hết cho x; 20 chia hết cho x
Suy ra x là ƯC(25; 20)
Ta có: 25 = 52; 20 = 22.5
ƯCLN(25; 20) = 5
ƯC(25; 20) = Ư(5) = {1; 5} nên x ∈ {1;5}
Mà x > 2 nên x = 5.
Vậy mỗi hộp bút chì màu có 5 chiếc.
Chẳng hạn, các ước của 6 (không kể chính nó) là 1; 2; 3; ta có: 1 + 2 + 3 = 6.
Vậy 6 là số hoàn hảo. Em hãy chỉ ra trong các số 10; 28; 496; số nào là số hoàn hảo.
Lời giải:
+) Các ước của 10 (không kể chính nó) là 1; 2; 5 và 1 + 2 + 5 = 8 ≠ 10 nên 10 không là số hoàn hảo.
+) Các ước của 28 (không kể chính nó) là: 1; 2; 4; 7; 14 và 1 + 2 + 4 + 7 + 14 = 28 nên 28 là số hoàn hảo.
+) Các ước của 496 (không kể chính nó) là 1; 2; 4; 8; 16; 31; 62; 124; 248 và 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496 nên 496 là số hoàn hảo.
Vậy trong các số trên có 28 và 496 là số hoàn hảo.
Lời giải:
Vì 480 ⁝ a và 720 ⁝ a nên a là ước chung của 480 và 720
Mà a lớn nhất nên a = ƯCLN(480; 720)
Ta có:
480 = 25.3.5
720 = 24.32.5
+) Ta chọn ra các thừa số nguyên tố chung là: 2; 3 và 5.
+) Số mũ nhỏ nhất của 2 là 4, số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1
ƯCLN(480; 720) = 24.3. 5 = 240.
Vậy số tự nhiên a lớn nhất là 240.
Lời giải:
a) Ta có:
21 = 3.7; 36 = 22.32
+) Thừa số nguyên tố chung là 3 với số mũ nhỏ nhất là 1 nên ƯCLN(21, 36) = 3.
Do đó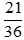 
không là phân số tối giản.
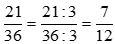. Ta được 
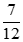là phân số tối giản vì ƯCLN(7, 12) = 1
b) Ta có:
23 = 23; 73 = 73
+) Không có thừa số nguyên tố chung nên ƯCLN(23, 73) = 1.
Do đó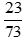 
là phân số tối giản.
Lời giải:
Giả sử cặp số cần tìm là a và b với a,b ≠ 0 . Vì ƯCLN của hai số đó là 17 ⇒ a và b chia hết cho 17 hay a và b đều là bội của 17.
B(17) = {0; 17; 34; 51; 68; …}
Vì các cặp số tự nhiên khác 0, không vượt quá 60 nên a và b thuộc {17; 34; 51}
Do đó ta có các cặp số (a; b) là (17; 34); (17; 51); (34; 51)
Thử lại: ƯCLN(17; 34) = 17 nên (17; 34) thỏa mãn
ƯCLN(17; 51) = 17 nên (17; 51) thỏa mãn
ƯCLN(34; 51) = 17 nên (34; 51) thỏa mãn
Vậy các cặp số cần tìm là (17; 34); (17; 51); (34; 51)
Lời giải:
Vì ƯCLN(a, b) = 16 ⇒ a và b là bội của 16, ta giả sử a = 16m; b = 16n với
ƯCLN(m, n) = 1 và do các số tự nhiên khác 0 nên m,n ∈ N*
Ta có a + b = 96 nên 16. m + 16. n = 96
16. (m + n) = 96
m + n = 96: 16
m + n = 6
Ta có bảng sau:
|
m |
1 |
2 |
3 |
4 |
5 |
|
n |
5 |
4 |
3 |
2 |
1 |
|
ƯCLN(m, n) = 1 |
TM |
KTM |
KTM |
KTM |
TM |
+) Với m = 1; n = 5 ta được a = 1. 16 = 16; b = 5. 16 = 80
+) Với m = 5; n = 1, ta được a = 5. 16 = 80; b = 1. 16 = 16
Vậy các cặp số (a; b) thỏa mãn là (16; 80); (80; 16)
Lời giải:
Vì ƯCLN của hai số đó là 8 nên hai số đó là bội của 8, ta giả sử a = 8m; b = 8n với ƯCLN(m, n) = 1 và do cặp số tự nhiên khác 0 nên m,n ∈ N*
Tích của hai số là 384 nên a.b = 384 hay 8m. 8n = 384
64. m. n = 384
m. n = 384: 64
m. n = 6
Ta có 6 = 1. 6 = 2. 3
Do đó (m; n) ∈ {(1;6);(6;1);(2;3);(3;2)}
Ta có bảng sau:
|
m |
1 |
6 |
2 |
3 |
|
n |
6 |
1 |
3 |
2 |
|
a = 8m |
8 |
48 |
16 |
24 |
|
b = 8n |
48 |
8 |
24 |
16 |
Vậy các cặp số tự nhiên thỏa mãn đề bài là (8; 48); (48; 8); (16; 24); (24; 16).
Xem thêm các bài giải SBT Toán 6 Kết nối tri thức hay, chi tiết khác: