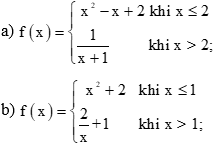Giải SBT Toán 11 (Chân trời sáng tạo) Bài 1: Đạo hàm

Sách bài tập Toán 11 Bài 1: Đạo hàm

Bài 1 trang 38 SBT Toán 11 Tập 2: Cho hàm số $y=\sqrt[3]{x}$. Chứng minh rằng $y^{\text{'}}\left(x\right)=\frac{1}{3\sqrt[3]{x^2}}\left(x\ne 0\right)$.

Lời giải:

Với $x_0\ne 0$, ta có:

$y^{\text{'}}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{\sqrt[3]{x}-\sqrt[3]{x_0}}{x-x_0}$

=$\underset{x\to x_0}{\lim }\frac{\sqrt[3]{x}-\sqrt[3]{x_0}}{\left(\sqrt[3]{x}-\sqrt[3]{x_0}\right)\left(\sqrt[3]{x^2}+\sqrt[3]{x{x}_0}+\sqrt[3]{{x_0}^2}\right)}$

$=\underset{x\to x_0}{\lim }\frac{1}{\sqrt[3]{x^2}+\sqrt[3]{x{x}_0}+\sqrt[3]{{x_0}^2}}=\frac{1}{3\sqrt[3]{{x_0}^2}}$.

Vậy $y^{\text{'}}\left(x\right)=\frac{1}{3\sqrt[3]{x^2}}\left(x\ne 0\right)$.

Bài 2 trang 38 SBT Toán 11 Tập 2: Cho parabol (P) có phương trình $y=x^2$. Tìm hệ số góc của tiếp tuyến của parabol (P).

a) Tại điểm (−1; 1);

b) Tại giao điểm của (P) với đường thẳng y = −3x + 2.

Lời giải:

Ta có $y^{\text{'}}=2x$.

a) Phương trình tiếp tuyến của (P) tại điểm (−1; 1) có hệ số góc $y^{\text{'}}(-1)=2.\left(-1\right)=-2$.

b) Gọi giao điểm của (P) với đường thẳng y = −3x + 2 là M(x₀; y₀).

Ta có $x_0^2=-3x_0+2\iff x_0^2+3x_0-2=0$

$\iff x_0=\frac{-3+\sqrt{17}}{2}$; $x_0=\frac{-3-\sqrt{17}}{2}$.

•Với $x_0=\frac{-3+\sqrt{17}}{2}$, hệ số góc của tiếp tuyến là $y^{\text{'}}\left(\frac{-3+\sqrt{17}}{2}\right)=-3+\sqrt{17}$.

•Với $x_0=\frac{-3-\sqrt{17}}{2}$, hệ số góc của tiếp tuyến là $y^{\text{'}}\left(\frac{-3-\sqrt{17}}{2}\right)=-3-\sqrt{17}$.

Bài 3 trang 39 SBT Toán 11 Tập 2: Xét tính liên tục, sự tồn tại đạo hàm và tính đạo hàm (nếu có) của các hàm số sau đây trên ℝ.

Lời giải:

a) Ta có

• $\underset{x\to 2^{+}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }\frac{1}{x+1}=\frac{1}{2+1}=\frac{1}{3}$;

• $\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{-}}{\lim }\left(x^2-x+2\right)=2^2-2+2=4$.

Vì $\underset{x\to 2^{+}}{\lim }f\left(x\right)=\frac{1}{3}\ne 4=\underset{x\to 2^{-}}{\lim }f\left(x\right)$ nên f(x) gián đoạn tại 2, do đó f(x) không có đạo hàm tại 2.

b) Ta có

• $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(\frac{2}{x}+1\right)=\frac{2}{1}+1=3$;

• $\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(x^2+2\right)=1^2+2=3$.

Vì $\underset{x\to 1^{+}}{\lim }f\left(x\right)=3=\underset{x\to 1^{-}}{\lim }f\left(x\right)$ nên f(x) liên tục tại 1.

Ta lại có

• $\underset{x\to 1^{-}}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}=\underset{x\to 1^{-}}{\lim }\frac{x^2+2x-3}{x-1}$

$=\underset{x\to 1^{-}}{\lim }\frac{\left(x-1\right)\left(x+3\right)}{x-1}=\underset{x\to 1^{-}}{\lim }\left(x+3\right)=1+3=4$.

• $\underset{x\to 1^{+}}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}=\underset{x\to 1^{+}}{\lim }\frac{\frac{2}{x}\text{+1}-3}{x-1}$

$=\underset{x\to 1^{+}}{\lim }\frac{\frac{2}{x}-2}{x-1}=\underset{x\to 1^{+}}{\lim }\frac{2-2x}{x\left(x-1\right)}$

$=\underset{x\to 1^{+}}{\lim }-\frac{2}{x}=\frac{-2}{1}=-2$.

Vì $\underset{x\to 1^{-}}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}\ne \underset{x\to 1^{+}}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}$ nên không tồn tại $\underset{x\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}$.

Vậy f(x) không có đạo hàm tại x = 1.

Bài 4 trang 39 SBT Toán 11 Tập 2: Gọi (C) là đồ thị của hàm số y = x³ − 2x² +1. Viết phương trình tiếp tuyến của (C) sao cho tiếp tuyến đó

a) Song song với đường thẳng y = −x + 2;

b) Vuông góc với đường thẳng $y=-\frac{1}{4}x-4$;

c) Đi qua điểm A(0; 1).

Lời giải:

Ta có $y^{\text{'}}=(x^3-2x^2+1{)}^{\text{'}}=3x^2-2.2x=3x^2-4x$.

a) Gọi d₁ là tiếp tuyến cần tìm của (C) và M₀(x₀; y₀) là tiếp điểm của (C) và d₁.

Vì d₁ song song với đường thẳng y = −x + 2 nên $y^{\text{'}}\left(x_0\right)=-1$.

Suy ra $3x_0^2-4x_0=-1\iff 3x_0^2-4x_0+1=0\iff x_0=1$ hoặc $x_0=\frac{1}{3}$.

− Với $x_0=1$, phương trình tiếp tuyến tại điểm $M_0\left(1;0\right)$ có hệ số góc $y^{\text{'}}\left(1\right)=-1$ là:

$y-y_0=y^{\text{'}}\left(x_0\right)\left(x-x_0\right)$

$\iff y-0=-1\left(x-1\right)$$\iff y=-x+1$.

− Với $x_0=\frac{1}{3}$, phương trình tiếp tuyến tại điểm $M_0\left(\frac{1}{3};\frac{22}{27}\right)$ có hệ số góc $y^{\text{'}}\left(\frac{1}{3}\right)=-1$ là:

$y-y\left(\frac{1}{3}\right)=y^{\text{'}}\left(\frac{1}{3}\right)\left(x-\frac{1}{3}\right)$

$\iff y-\frac{22}{27}=-1\left(x-\frac{1}{3}\right)$

$\iff y=-x+\frac{31}{27}$

Vậy tiếp tuyến của (C) song song với đường thẳng y = −x + 2 là: $d_1:y=-x+1$ và $d_2:y=-x+\frac{31}{27}$.

b) Gọi d₁ là tiếp tuyến cần tìm của (C) và M₀(x₀; y₀) là tiếp điểm của (C) và d₁.

Vì d₁ vuông góc với đường thẳng $y=-\frac{1}{4}x-4$ nên $y^{\text{'}}\left(x_0\right).\left(-\frac{1}{4}\right)=-1\iff y^{\text{'}}\left(x_0\right)=4$.

Suy ra $3x_0^2-4x_0=4\iff 3x_0^2-4x_0-4=0\iff x_0=2$ hoặc $x_0=-\frac{2}{3}$.

− Với $x_0=2$, phương trình tiếp tuyến tại điểm $M_0\left(2;1\right)$ có hệ số góc $y^{\text{'}}\left(2\right)=4$ là:

$y-y_0=y^{\text{'}}\left(x_0\right)\left(x-x_0\right)$

$\iff y-1=4\left(x-2\right)$

$\iff y=4x-7$.

− Với $x_0=-\frac{2}{3}$, phương trình tiếp tuyến tại điểm $M_0\left(-\frac{2}{3};-\frac{5}{27}\right)$ có hệ số góc $y^{\text{'}}\left(-\frac{2}{3}\right)=4$ là:

$y-y\left(-\frac{2}{3}\right)=y^{\text{'}}\left(-\frac{2}{3}\right)\left(x+\frac{2}{3}\right)$

$\iff y-\left(-\frac{5}{27}\right)=4\left(x+\frac{2}{3}\right)$

$\iff y=4x+\frac{67}{27}$

Vậy tiếp tuyến của (C) song song với đường thẳng y = −x + 2 là: $d_1:y=4x+9$ và $d_2:y=4x+\frac{67}{27}$.

c) Gọi d₁ là tiếp tuyến cần tìm của (C) đi qua điểm A(0; 1) tại tiếp điểm M(x₀;f(x₀)).

Phương trình tiếp tuyến d₁ của (C) có dạng:

$y-y_0=y^{\text{'}}\left(x_0\right)\left(x-x_0\right)$

$\iff y=y^{\text{'}}\left(x_0\right)x+y_0-y^{\text{'}}\left(x_0\right)x_0$

$\iff y=\left(3{x_0}^2-4x_0\right)x+({x_0}^3-2{x_0}^2+1)-\left(3{x_0}^2-4x_0\right)x_0$

$\iff y=\left(3{x_0}^2-4x_0\right)x+\left(-2{x_0}^3+2{x_0}^2+1\right)$

Vì d₁ đi qua điểm A(0; 1) nên

$1=\left(3{x_0}^2-4x_0\right).0+\left(-2{x_0}^3+2{x_0}^2+1\right)$

$\iff 1=-2{x_0}^3+2{x_0}^2+1$

$\iff 0=-2{x_0}^3+2{x_0}^2$

$\iff x_0=1$ ; $x_0=0$

− Với $x_0=1$, phương trình đường thẳng d₁ là:

$y=\left({3.1}^2-4.1\right)x+1=-x+1$.

− Với $x_0=0$, phương trình đường thẳng d₁ là:

$y=\left({3.0}^2-4.0\right)x+1=1$.

Vậy tiếp tuyến của (C) đi qua điểm A(0; 1) là: $d_1:y=-x+1$ và $d_2:y=1$.

Bài 5 trang 39 SBT Toán 11 Tập 2: Một vật chuyển động có quãng đường được xác định bởi phương trình $s\left(t\right)=2t^2+5t+2$, trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời tại điểm t = 4.

Lời giải:

Ta có $s^{\text{'}}\left(t\right)={\left(2t^2+5t+2\right)}^{\text{'}}=2.2t+5=4t+5$.

Vận tốc tức thời tại điểm t = 4 là $s^{\text{'}}\left(4\right)=4.4+5=21$.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: