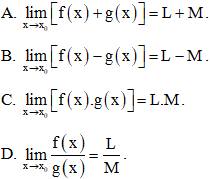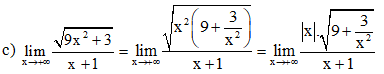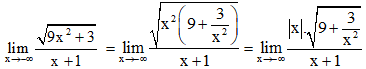Giải SBT Toán 11 Bài 2: Giới hạn của hàm số
Bài 12 trang 74 SBT Toán 11 Tập 1: Giả sử và (L, M ∈ ℝ). Phát biểu nào sau đây là sai?
Lời giải:
Đáp án đúng là: D
Với và (L, M ∈ ℝ) thì (nếu M ≠ 0).
Do vậy đáp án D sai vì thiếu điều kiện M ≠ 0.
A. Nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L thì .
B. Nếu với dãy số (xn) bất kì, xn → x0, ta có f(xn) → L thì .
C. Nếu với dãy số (xn) bất kì, x0 < xn < b và xn → L, ta có f(xn) → x0 thì .
D. Nếu với dãy số (xn) bất kì, xn < x0 và xn → x0, ta có f(xn) → L thì .
Lời giải:
Đáp án đúng là: A
Theo lí thuyết, ta có: Cho hàm số y = f(x) xác định trên khoảng (x0; b), nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L thì .
Bài 14 trang 75 SBT Toán 11 Tập 1: Với c, k là các hằng số và k nguyên dương thì
A. .
B. .
C. .
D. hoặc .
Lời giải:
Đáp án đúng là: A
Với c, k là các hằng số và k nguyên dương, ta luôn có .
Bài 15 trang 75 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng?
A. Nếu thì .
B. Nếu thì L ≥ 0.
c. Nếu f(x) ≥ 0 và thì L ≥ 0 và .
D. Nếu thì L ≥ 0 và .
Lời giải:
Đáp án đúng là: C
Theo lí thuyết ta có: Nếu f(x) ≥ 0 và thì L ≥ 0 và .
A. Nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L thì .
B. Nếu với dãy số (xn) bất kì, xn < a và xn → +∞, ta có f(xn) → L thì .
C. Nếu với dãy số (xn) bất kì, xn > a, ta có f(xn) → L thì .
D. Nếu với dãy số (xn) bất kì, xn > a và xn → L, ta có f(xn) →+∞ thì .
Lời giải:
Đáp án đúng là: A
Theo lí thuyết, ta có: Cho hàm số y = f(x) xác định trên khoảng (a ; + ∞), nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L thì .
Bài 17 trang 75 SBT Toán 11 Tập 1: Sử dụng định nghĩa, chứng minh rằng:
a) .
b) .
Lời giải:
a) Xét hàm số f(x) = x3. Giả sử (xn) là dãy số bất kì, thỏa mãn limxn = – 2.
Ta có limf(xn) = .
Vậy .
b) Xét hàm số .
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ≠ – 2 và lim xn = – 2.
Ta có .
Vậy .
Bài 18 trang 75 SBT Toán 11 Tập 1: Cho , chứng minh rằng:
a) ;
b) ;
c) .
Lời giải:
a) .
b) .
c) .
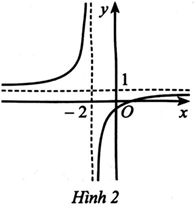
Bài 19 trang 76 SBT Toán 11 Tập 1: Quan sát đồ thị hàm số ở Hình 2 và cho biết các giới hạn sau: .
Lời giải:
Dựa vào đồ thị hàm số, ta có:
;
;
;
.
Bài 20 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Lời giải:
a) = – 4 – 3 + 1 = – 6.
b) .
c) Vì .
Do đó, .
d) Vì
và 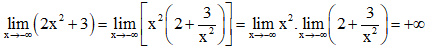
Do đó, .
e) Vì ; và x – 2 > 0 với mọi x > 2.
Do đó, .
g) Vì ; và x + 2 > 0 với mọi x > – 2.
Do đó, .
Bài 21 trang 76 SBT Toán 11 Tập 1: Tính các giới hạn sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Lời giải:
a) .
b) .
c)
d)
.
e) .
g) .
Bài 22 trang 76 SBT Toán 11 Tập 1: Cho . Tính:
a) ;
b) .
Lời giải:
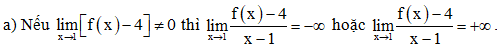
Điều này mâu thuẫn với giả thiết .
b) Ta có .
Bài 23 trang 76 SBT Toán 11 Tập 1: Cho hàm số f(x) thoả mãn . Tính .
Lời giải:
Ta có
.
Vậy .
Bài 24 trang 76 SBT Toán 11 Tập 1: Cho số thực a và hàm số (x) thoả mãn . Chứng minh rằng:
.
Lời giải:
Ta có
.
Vậy .
Lời giải:
Ta có g(10) = 45 . 102 – 103.
Khi đó
.
Vậy = 600.
Từ kết quả trên, ta thấy tốc độ tăng người bệnh ngay tại thời điểm t = 10 ngày là 600 người/ngày.
Xem thêm lời giải bài tập SBT Toán 11 Cánh diều hay, chi tiết khác: