Giải SBT Toán 10 (Kết nối tri thức) Bài 22: Ba đường conic

Giải Sách bài tập Toán 10 Bài 22: Ba đường conic

Giải SBT Toán 10 trang 46 Tập 2

Bài 7.28 trang 46 SBT Toán 10 Tập 2: Cho elip (E) có phương trình $\frac{x^2}{36}+\frac{y^2}{16}=1$ . Tìm tiêu điểm và tiêu cự của elip.

Lời giải:

Dựa vào phương trình chính tắc $\frac{x^2}{36}+\frac{y^2}{16}=1$  của (E) ta có

$\left\{\begin{array}{c}{a}^2=36\\ b^2=16\end{array}\right.\Rightarrow c=\sqrt{a^2-b^2}=2\sqrt{5}$

Vậy (E) có hai tiêu điểm là: $F_1\left(-2\sqrt{5};0\right),F_2\left(2\sqrt{5};0\right)$ và có tiêu cự là: $2c=4\sqrt{5}$ .

Bài 7.29 trang 46 SBT Toán 10 Tập 2: Cho hypebol (H) có phương trình $\frac{x^2}{16}-\frac{y^2}{20}=1$. Tìm tiêu điểm và tiêu cự của hypebol.

Lời giải:

Dựa vào phương trình chính tắc $\frac{x^2}{16}-\frac{y^2}{20}=1$  của (H) ta có

$\left\{\begin{array}{c}{a}^2=16\\ b^2=20\end{array}\right.\Rightarrow c=\sqrt{a^2+b^2}=6$

Vậy (H) có hai tiêu điểm là F₁ (–6; 0), F₂(6; 0) và có tiêu cự là 2c = 12.

Bài 7.30 trang 46 SBT Toán 10 Tập 2: Cho parabol (P) có phương trình y² = 4x. Tìm tiêu điểm và đường chuẩn của parabol.

Lời giải:

Dựa vào phương trình chính tắc y² = 4x của (P) ta có:

2p = 4 ⇔ p = 2 ⇔ $\frac{p}{2}=1$  .

Vậy (P) có tiêu điểm là F(1; 0) và có đường chuẩn là Δ: x = –1.

Bài 7.31 trang 46 SBT Toán 10 Tập 2: Viết phương trình chính tắc của elip (E), biết (E) đi qua điểm A(6; 0) và có tiêu cự bằng 8.

Lời giải:

Phương trình chính tắc của (E) có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$  (trong đó a > b > 0)

Vì (E) đi qua điểm A(6; 0) nên ta có $\frac{6^2}{a^2}+\frac{0^2}{b^2}=1$  ⇔ a² = 6² 

Do (E) có tiêu cự là 2c = 8 nên ta có c = 4 ⇒ b² = a² – c² = 6² – 4² = 20.

Vậy phương trình chính tắc của (E) là: $\frac{x^2}{36}+\frac{y^2}{20}=1$ .

Bài 7.32 trang 46 SBT Toán 10 Tập 2: Viết phương trình chính tắc của hypebol (H), biết (H) đi qua điểm $M\left(3\sqrt{2};-4\right)$ và có một tiêu điểm là F₂(5; 0).

Lời giải:

Phương trình chính tắc của (H) có dạng: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$   (trong đó a, b > 0)

Do (H) có một tiêu điểm là F₂(5; 0) nên ta có:

c = 5 ⇒ b² + a² = c² = 25 ⇔ a² = 25 – b²

Vì (H) đi qua điểm $M\left(3\sqrt{2};4\right)$ nên ta có

$\frac{{\left(3\sqrt{2}\right)}^2}{a^2}-\frac{4^2}{b^2}=1\iff \frac{18}{a^2}-\frac{16}{b^2}=1$            (1)

Đặt t = b² (t > 0) ⇒ a² = 25 – t. Thay vào (1) ta được

$\frac{18}{25-t}-\frac{16}{t}=1$

⇒ 18t – 16(25 – t) = (25 – t)t

⇔ 18t – 400 + 16t = 25t – t²

⇔ t² + 9t – 400 = 0

⇔ t = 16 (thỏa mãn) hoặc t = –25 (không thỏa mãn)

Do đó, b² = t = 16, a² = 25 – t = 9.

Vậy phương trình chính tắc của (H) là: $\frac{x^2}{9}-\frac{y^2}{16}=1$ .

Bài 7.33 trang 46 SBT Toán 10 Tập 2: Viết phương trình chính tắc của parabol (P), biết rằng (P) có đường chuẩn là đường thẳng Δ: x + 4 = 0. Tìm toạ độ điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của (P) bằng 5.

Lời giải:

Phương trình chính tắc của (P) có dạng y² = 2px, trong đó p > 0.

Vì (P) có đường chuẩn là Δ: x + 4 = 0 ⇔ x = –4 ⇔ –p : 2 = –4 ⇔ p = 8

Vậy phương trình chính tắc của (P) là y² = 16x.

Gọi M (x₀; y₀).

Vì M thuộc (P) nên ta có:

d(M, Δ) = MF = 5 với F là tiêu điểm của (P) và F(4; 0).

$\iff \frac{\left|x_0+4\right|}{\sqrt{1^2+0^2}}=5$

⇔ |x₀ + 4| = 5 (*)

TH1: x₀ + 4 ≥ 0 hay x₀ ≥ –4

 (*) ⇔  x₀ + 4 = 5  ⇔ x₀ = 1 (thỏa mãn)

TH2: x₀ + 4 < 0 hay x₀ < –4

 (*) ⇔  –x₀ – 4 = 5  ⇔ x₀ = –9 (thỏa mãn)

Với x₀ = –9, thay vào phương trình của (P) ta được y₀² = 16.(–9) = –144 < 0 (không thể tồn tại)

Với x₀ = 1, thay vào phương trình của (P) ta được y₀² = 16.1 = 16 ⇔ y₀  = ±4

Vậy M(1; 4) hoặc M(1; –4).

Bài 7.34 trang 46 SBT Toán 10 Tập 2: Cho parabol (P) có phương trình là y² = 16x. Gọi Δ là đường thẳng bất kì đi qua tiêu điểm F của (P) và không trùng với trục hoành. Chứng minh rằng Δ luôn cắt (P) tại hai điểm phân biệt A, B, đồng thời tích các khoảng cách từ A và B đến trục hoành không đổi.

Lời giải:

Gọi vectơ chỉ phương của Δ là $\overrightarrow{u_{\Delta }}=\left(a;b\right)$ . Vì Δ đi qua điểm F(4; 0) và Δ không trùng với trục Ox nên ta có b ≠ 0. Phương trình tham số của Δ là

$\left\{\begin{array}{c}x=4+at\\ y=0+bt=bt\end{array}\right.$.

Toạ độ giao điểm của Δ và (P) ứng với thoả mãn phương trình

(bt)² =16 . (4 + at) ⇔ b²t² – 16at – 64 = 0. (1)

Phương trình (1) có Δ’ = 64a² + 64b² > 0 (do b ≠ 0), suy ra phương trình (1) luôn có 2 nghiệm phân biệt. Vậy Δ luôn cắt (P) tại hai điểm phân biệt A, B.

Gọi A(4 + at₁; bt₁), B(4 + at₂; bt₂), trong đó t₁, t₂ là hai nghiệm của phương trình (1).

Ta có

$d\left(A,Ox\right).d\left(B,Ox\right)=\frac{\left|b{t}_1\right|}{\sqrt{0^2+1^2}}.\frac{\left|b{t}_2\right|}{\sqrt{0^2+1^2}}=\left|b^2.t_1{t}_2\right|$

Dựa vào phương trình (1). Theo định lí Vi–ét ta có: $t_1{t}_2=\frac{-64}{b^2}$ . Từ đó suy ra

$d\left(A,Ox\right).d\left(B,Ox\right)=\left|b^2.\frac{-64}{b^2}\right|=64$

Vậy tích các khoảng cách từ A và B đến trục hoành không đổi.

Bài 7.35 trang 46 SBT Toán 10 Tập 2: Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cao 2,8 m có thể đi qua hầm được không?

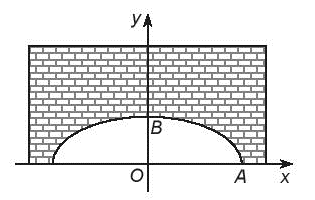
Lời giải:

Giả sử phương trình chính tắc của (E) là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$  (trong đó a > b > 0).

Vì chiều rộng của hầm là 12 m nên OA = 12 : 2 = 6 (m), do đó điểm A có tọa độ (6; 0).

Khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m nên OB = 3 m, do đó điểm B có tọa độ (0; 3).

Do các điểm B(0; 3) và A(6; 0) thuộc (E) nên thay vào phương trình của (E) ta có:

$$\begin{gathered} \frac{0^2}{a^2}+\frac{3^2}{b^2}=1\Rightarrow b^2=3^2=9 \\ \frac{6^2}{a^2}+\frac{0^2}{b^2}=1\Rightarrow a^2=6^2=36 \end{gathered}$$

Suy ra phương trình của (E) là

$\frac{x^2}{36}+\frac{y^2}{9}=1$.

Với những xe tải có chiều cao 2,8 m, chiều rộng của xe tải là 3 m, nếu xe chạy chính giữa hầm thì khoảng cách từ tâm xe tới mỗi bên xe khoảng 3 : 2 = 1,5 m, tương ứng với x = 1,5. Thay vào phương trình của elip để ta tìm ra độ cao y của điểm M (có hoành độ bằng 1,5 thuộc (E)) so với trục Ox.

$\frac{{x_M}^2}{36}+\frac{{y_M}^2}{9}=1$

Suy ra: $y_M=3.\sqrt{1-\frac{x_M^2}{36}}=3.\sqrt{1-\frac{{\mathrm{1,5}}^2}{36}}\approx \mathrm{2,905}>\mathrm{2,8}$

Kết luận: Ô tô tải có thể đi được qua hầm, tuy nhiên cần khuyến cáo ô tô phải đi vào chính giữa hầm.

Giải SBT Toán 10 trang 47 Tập 2

Bài 7.36 trang 47 SBT Toán 10 Tập 2: Cho điểm M(x₀; y₀) thuộc elip (E) có phương trình $\frac{x^2}{2}+\frac{y^2}{1}=1$ .

a) Tính MF₁² – MF₂²  theo x₀; y₀. Từ đó tính MF₁, MF₂, theo x₀; y₀.

b) Tìm điểm M sao cho MF₂ = 2MF₁.

c) Tìm M sao cho góc nhìn của M tới hai đểm F₁; F₂ (tức là góc $\widehat{F_{1}M{F}_2}$ ) là lớn nhất ?

Lời giải:

Từ phương trình chính tắc của (E) ta có

b = 1, $a=\sqrt{2},c=\sqrt{a^2-b^2}=\sqrt{2-1}=1$.

(E) có hai tiêu điểm là F₁(–1; 0); F₂(1; 0).

a)

Ta có:

MF₁² = (x₀ + 1)² + (y₀ – 0)² = (x₀ + 1)² + y₀²

MF₂² = (x₀ – 1)² + (y₀ – 0)² = (x₀ – 1)² + y₀²

MF₁² – MF₂²  

= (x₀ + 1)² + y₀²  – [(x₀ – 1)² + y₀²]

= (x₀ + 1)²  – (x₀ – 1)²

= x₀²  + 2x₀ + 1 – (x₀²  – 2x₀ + 1)

= 4x₀.

Mặt khác, do M thuộc (E) nên ta có:

MF₁ + MF₂ = 2a = $2\sqrt{2}$  (1)  

Mà: (MF₁ – MF₂)(MF₁ + MF₂) = MF₁² – MF₂²  

 $\Rightarrow M{F}_1-M{F}_2=\frac{M{F}_1^2-M{F}_1^2}{M{F}_1+M{F}_2}=\frac{4x_0}{2\sqrt{2}}=\sqrt{2}{x}_0$ (2)

Cộng hai vế của (1) và (2) ta có:

2MF₁ = $2\sqrt{2}$  + $\sqrt{2}{x}_0$

⇔ MF₁ =  $\sqrt{2}$ +  $\frac{x_0}{\sqrt{2}}$

⇒ MF₂ = $2\sqrt{2}-\sqrt{2}-\frac{x_0}{\sqrt{2}}=\sqrt{2}-\frac{x_0}{\sqrt{2}}$ .

b)

Sử dụng kết quả của phần a) ta có:

$M{F}_2=2M{F}_1\iff \sqrt{2}-\frac{x_0}{\sqrt{2}}=2\left(\sqrt{2}+\frac{x_0}{\sqrt{2}}\right)\iff \frac{3x_0}{\sqrt{2}}=-\sqrt{2}\iff x_0=-\frac{2}{3}$

Mặt khác do M thuộc (E) nên ta có:

$\frac{x_0^2}{2}+\frac{y_0^2}{1}=1\iff y_0^2=1-\frac{x_0^2}{2}=1-\frac{{\left(-\frac{2}{3}\right)}^2}{2}=\frac{7}{9}\iff \left[\begin{array}{c}{y}_0=\frac{\sqrt{7}}{3}\\ y_0=-\frac{\sqrt{7}}{3}\end{array}\right.$

Vậy $M\left(-\frac{2}{3};\frac{\sqrt{7}}{3}\right)$ hoặc $M\left(-\frac{2}{3};-\frac{\sqrt{7}}{3}\right)$ .

c)

Áp dụng định lí côsin trong tam giác MF₁F₂, ta có

$\cos \widehat{F_{1}M{F}_2}=\frac{M{F}_1^2+M{F}_2^2-F_1{F}_2^2}{2.M{F}_1.M{F}_2}$

$=\frac{{\left(\sqrt{2}+\frac{x_0}{\sqrt{2}}\right)}^2+{\left(\sqrt{2}-\frac{x_0}{\sqrt{2}}\right)}^2-2^2}{2.\left(\sqrt{2}+\frac{x_0}{\sqrt{2}}\right).\left(\sqrt{2}-\frac{x_0}{\sqrt{2}}\right)}=\frac{x_0^2}{4-x_0^2}$

Ta có: $\frac{x_0^2}{2}=1-y_0^2\le 1$  ⇔ 0 ≤ x₀² ≤ 2 ⇒ 4 – x₀² > 0.

Suy ra $\cos \widehat{F_{1}M{F}_2}\ge 0\Rightarrow \widehat{F_{1}M{F}_2}\le 90°$

Dấu bằng xảy ra khi và chỉ khi x₀ = 0 ⇒ y₀  = ±1

Vậy M(0; 1) hoặc M(0; –1) thì M nhìn hai tiêu điểm dưới góc nhìn lớn nhất.

Bài 7.37 trang 47 SBT Toán 10 Tập 2: Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là một tiêu điểm. Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm của Trái Đất đến Mặt Trăng.

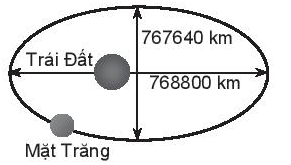
Lời giải:

Xét đường elip như hình vẽ:

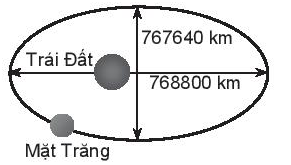
Theo đề bài: Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Nên ta có:

2a = 768 800 và 2b = 767 640

Do đó, a = 384 400 và b = 383 820.

Từ đó suy ra $c=\sqrt{a^2-b^2}=\sqrt{{384400}^2-{383820}^2}\approx 21108$ .

Vì vậy,

Khoảng cách lớn nhất từ tâm của Trái Đất đến Mặt Trăng là

a + c ≈ 384 400 + 21 108 = 405 508 (km)

Khoảng cách nhỏ nhất từ tâm của Trái Đất đến Mặt Trăng là:

a – c ≈ 384 400 – 21 108 = 363 292 (km).

Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài tập cuối chương 7

Bài 23: Quy tắc đếm

Bài 24: Hoán vị, chỉnh vị và tổ hợp