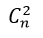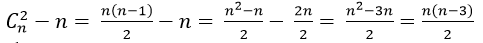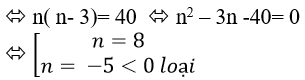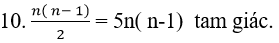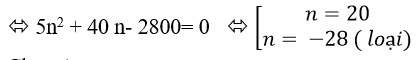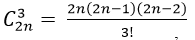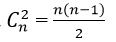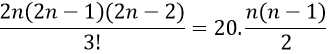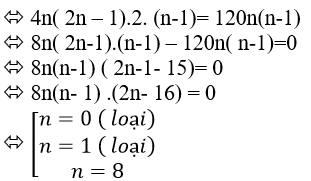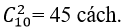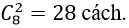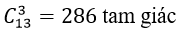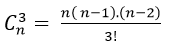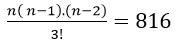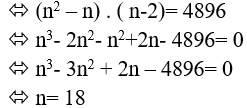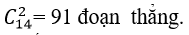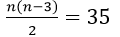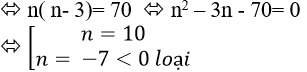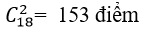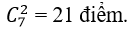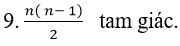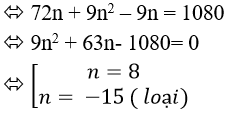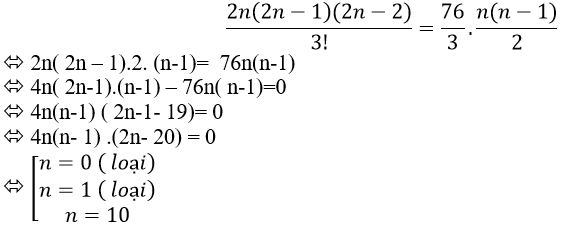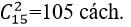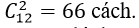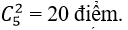Công thức tính tổ hợp (2024) chi tiết nhất

Công thức tính tổ hợp

I. Công thức

Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Mỗi tập hợp con của A có k phần tử được gọi là một tổ hợp chập k của n phần tử của A.

Công thức tổ hợp chập k của n

Công thức tính chất của tổ hợp:

II. Ví dụ minh hoạ

Ví dụ 1: Số tam giác xác định bởi các đỉnh của một đa giác lồi 16 cạnh.

A.560    B.420    C.240    D.280

Hướng dẫn giải :

Đáp án : A

Đa giác lồi đã cho có 16 cạnh nên đa giác này có 16 đỉnh.

Một tam giác được xác định nếu biết ba đỉnh của nó.

Do đó số tam giác xác định bởi các đỉnh của đa giác lồi đã cho là: 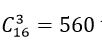 tam giác .

Ví dụ 2: Cho một đa giác có 12 cạnh. Hỏi đa giác này có bao nhiêu đường chéo.

A.48    B.51    C.54     D.62

Hướng dẫn giải :

Đáp án : C

Đa giác đã cho có 12 cạnh nên có 12 đỉnh.

Số đoạn thẳng được tạo ra từ 12 đỉnh này là: 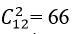 đoạn thẳng.

Mà đa giác này có 12 cạnh nên đa giác này có số đường chéo là: 66- 12= 54 đường chéo.

Chú ý: Số cạnh+ số đường chéo =số đoạn thẳng nối 2 đỉnh bất kì.

Ví dụ 3: Cho đa giác lồi n đỉnh (n≥4) . Hỏi đa giác đã cho có bao nhiêu đường chéo?

Hướng dẫn giải :

Đáp án : C

Do đa giác này có n đỉnh nên đa giác này có n cạnh.

Từ n đỉnh của đa giác ta có số đoạn thẳng có đầu mút; cuối mút là n đỉnh này là: 

⇒ Số đường chéo của đa giác là:

Ví dụ 4: Cho một đa giác có n đỉnh. Biết rằng đa giác này có 20 đường chéo. Tìm n?

A.7    B.8     C.10     D.12

Hướng dẫn giải :

Đáp án : B

+ Do đa giác này có n đỉnh nên đa giác này có n cạnh .

+ Từ n đỉnh của đa giác ta có số đoạn thẳng có đầu mút; cuối mút là n đỉnh này là: 

⇒ Số đường chéo của đa giác là:

+ Theo giả thiết ta có: (n(n-3))/2=20

Vậy đa giác đã cho có 8 đỉnh.

Ví dụ 5: Số giao điểm tối đa của 12 đường thẳng phân biệt là:

A.66    B.132    C.120    D.45

Hướng dẫn giải :

Đáp án : A

Hai đường thẳng phân biệt có tối đa 1 giao điểm.

⇒ số giao điểm tối đa của 12 đường thẳng là: 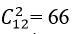 điểm

Ví dụ 6: Cho một đường tròn và 5 đường thẳng phân biệt. Hỏi có tối đa bao nhiêu giao điểm?

A.10    B.15    C. 20    D. 25

Hướng dẫn giải :

Đáp án : C

+ Ta tính số giao điểm tối đa của 5 đường thẳng:

Hai đường thẳng phân biệt có tối đa 1 giao điểm

⇒ số giao điểm tối đa của 5 đường thẳng là: .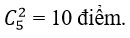

+ Ta tính số giao điểm tối đa của 5 đường thẳng với đường tròn.

Một đường thẳng cắt đường tròn tối đa tại hai điểm

⇒ 5 đường thẳng cắt đường tròn tối đa: 2.5= 10 điểm

⇒ Số giao điểm tối đa của 5 đường thẳng và đường tròn là:10 + 10= 20 điểm

Ví dụ 7: Cho hai đường thẳng song song a và b. Trên đường thẳng a cho 6 điểm phân biệt, trên đường thẳng b cho 7 điểm phân biệt. Hỏi có bao nhiêu tam giác có các đỉnh là các điểm đã cho trên hai đường a và b.

A.364    B.231    C.288    D.210

Hướng dẫn giải :

Đáp án : B

- Trường hợp 1. Tam giác có 2 đỉnh nằm trên a và 1 đỉnh thuộc b

   + Có 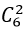 = 15 cách chọn 2 đỉnh thuộc đường thẳng a.

   + Có 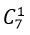 = 7 cách chọn 1 đỉnh thuộc b.

   + Theo quy tắc nhân có : 15.7= 105 tam giác.

- Trường hợp 2. Tam giác có 1 đỉnh nằm trên a và 2 đỉnh thuộc b

   + Có 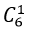 = 6 cách chọn 1 đỉnh thuộc đường thẳng a.

   + Có 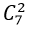 = 21 cách chọn 2 đỉnh thuộc b.

   + Theo quy tắc nhân có : 6.21= 126 tam giác.

Kết hợp hai trường hợp ta có : 105 + 126= 231 tam giác

Ví dụ 8: Cho hai đường thẳng d₁ và d₂ song song với nhau. Trên d₁ có 10 điểm phân biệt, trên d₂ có n điểm phân biệt ( n>1). Biết có 2800 tam giác có đỉnh là các điểm nói trên.Tìm n?

A.20    B.21    C.30    D.32

Hướng dẫn giải :

Đáp án : A

- Trường hợp 1. Tam giác có 2 đỉnh nằm trên d₁ và 1 đỉnh thuộc d₂

   + Có 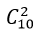 = 45 cách chọn 2 đỉnh thuộc đường thẳng d₁.

   + Có 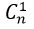 = n cách chọn 1 đỉnh thuộc d₂.

   + Theo quy tắc nhân có : 45.n tam giác.

- Trường hợp 2. Tam giác có 1 đỉnh nằm trên d₁ và 2 đỉnh thuộc d₂

   + Có 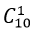 =10 cách chọn1 đỉnh thuộc đường thẳng d₁.

   + Có 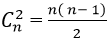 cách chọn 2 đỉnh thuộc d₂.

   + Theo quy tắc nhân có : 

Do đó số tam giác được tạo ra là : 45n+5n( n-1)

Theo đề bài ta có : 45n + 5n( n-1)= 2800

Ví dụ 9: Cho đa giác đều A₁A₂....A_2n nội tiếp trong đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm A₁ ;A₂ ;.... ; A_2n gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm A₁ ;A₂ ;.... ; A_2n. Tìm n?

A.3    B.6    C.8    D.12

Hướng dẫn giải :

Đáp án : C

+ Số tam giác có đỉnh là 3 trong số 2n điểm đã cho là: 

+ Do đa giác đều A₁A₂....A_2n nội tiếp trong đường tròn tâm O nên các đoạn thẳng A₁A_n+1; A₂A_{n+ 2};...; A_nA_2n là n đường kính .

+ Số các hình chữ nhật có đỉnh là 4 trong 2n điểm A₁ ;A₂ ;.... ; A_2n là 

( Cứ hai đường kính cho ta một hình chữ nhật nên số các hình chữ nhật thỏa mãn chính bằng số cách chọn 2 đường kính trong n đường kính).

+ Theo đầu bài ta có phương trình :

Vậy n= 8.

Ví dụ 10: Cho 10 đường thẳng song song lần lượt cắt 8 đường thẳng song song khác. Hỏi có bao nhiêu hình bình hành được tạo thành từ các đường thẳng trên.

A.45    B.28    C.73    D.1260

Hướng dẫn giải :

Đáp án : D

Ta chia các đường thẳng đã cho thành 2 nhóm:

+ Nhóm 1: là 10 đường thẳng song song với nhau

+ Nhóm 2: Là 8 đường thẳng song song với nhau

Tứ giác có các cạnh đối diện song song với nhau là hình bình hành.

+ Bước 1: Chọn 2 đường thẳng nhóm 1 có: 

+ Bước 2: Chọn 2 đường thẳng nhóm 2 có: 

Số hình bình hành được tạo ra là; 45.28= 1260 hình

Ví dụ 11: Trong mặt phẳng tọa độ cho đa giác (H): A₁A₂...A₁₀. Hỏi từ các đỉnh của đa giác (H) ta lập được bao nhiêu tam giác có đúng 1 cạnh của (H)?

A.54    B.64    C.60    D.72

Hướng dẫn giải :

Đáp án : C

Đa giác A₁A₂..A₁₀ là đa giác có 10 đỉnh và có 10 cạnh .

Giả sử tam giác A_iA_jA_k ( 1≤i,j,k≤10) có đúng 1 cạnh của ( H).

Giả sử A_iA_j là một cạnh của ( H). Khi đó số cách chọn cạnh này là: 10( vì đa giác (H) có 10 cạnh).

Số cách chọn đỉnh còn lại A_k là 6 cách ( đỉnh này khác A_i; A_j và khác hai đỉnh liền kề với A_i,A_j )

Theo quy tắc nhân; số tam giác thỏa mãn là 10.6= 60 tam giác.

Ví dụ 12: Trong mặt phẳng cho đa giác đều (H) có 20 cạnh. Có bao nhiêu tam giác có 3 đỉnh là các đỉnh của (H) nhưng không có cạnh nào là cạnh của (H) ?

A.4760    B.3720    C.3600    D.2400

Hướng dẫn giải :

Đáp án : A

Do đa giác đã cho có 20 cạnh nên đa giác này có 20 đỉnh là A₁; A₂; ..; A₂₀.

+ Bước 1. Chọn đỉnh thứ nhất A_i: có 20 cách.

+ Bước 2. Chọn đỉnh thứ hai A_j: đỉnh thứ 2 khác đỉnh thứ nhất và khác với đỉnh liền kề với A_i ( chú ý tam giác cần lập không có cạnh nào của ( H)) nên có 17 cách chọn đỉnh A_j

+ Bước 3. Chọn đỉnh thứ ba A_k: khác đỉnh thứ nhất - thứ hai; khác 2 đỉnh liền kề A_i; khác 2 đỉnh liền kề A_j nên có 14 cách chọn A_k.

Theo quy tắc nhân có: 20.17.14= 4760 tam giác thỏa mãn.

III. Bài tập vận dụng

BT1: Có 10 cuố sách toán khác nhau. Chọn ra 4 cuốn hỏi có bao nhiêu cách.

Hướng dẫn giải:
Mỗi cách chọn ra 4 trong số 10 cuốn sách là một tổ hợp chập 4 của 10.

Vậy có  = 210 (cách chọn).

BT2: Từ tập hợp X= {0; 1; 2; 3; 4; 5} có thể lập được mấy số tự nhiên có 4 chữ số khác nhau.

Hướng dẫn giải:

BT3: Có 6 chữ số tất cả, mà lập số có 5 chữ số khác nhau nên số cần lập được tạo thành từ các chữ số: 0,1,2,3,4 hoặc 0,1,2,3,5 hoặc 0,1,2,4,5 hoặc 0,1,3,4,5 hoặc 0,2,3,4,5 hoặc 1,2,3,4,5.

Hướng dẫn giải:

Trong 6 trường hợp này, chỉ có hai trường hợp thỏa mãn yêu cầu a1+a2+a3+a4+a5 chia hết cho 3. Do đó ta xét hai trường hợp:

- TH1. Số cần lập được tạo thành từ các chữ số 1,2,3,4,5. Mỗi số cần lập tương ứng với một hoán vị của 5 phần tử, nên có 5!=120 số.

- TH2. Số cần lập được tạo thành từ các chữ số 0,1,2,4,5. Ta tiến hành 2 bước:

+ Bước 1. Chọn a1≠0: Có 4 cách chọn.

+ Sắp xếp 4 chữ số còn lại vào 4 vị trí còn lại: Có 4!=24 cách.
Theo qui tắc nhân, TH2 có 4.24=96 số.

Vậy, có tất cả 120+96=216 số thỏa mãn yêu cầu.

BT4: Có bao nhiêu số tự nhiên có 5 chữ số, chia hết cho 2 mà chữ số đầu tiên của nó cũng là số chẵn?

Hướng dẫn giải: 

Vì đề bài không có yêu cầu các chữ số phải khác nhau nên chúng ta chọn thoải mái.

+ Bước 1. Chọn chữ số đứng đầu tiên, chữ số này phải khác 0 và chẵn, nên có 4 cách chọn (một trong các chữ số 2,4,6,8).

+ Bước 2. Chọn chữ số đứng thứ hai là một trong các chữ số 0,1,2,…,9 nên có 10cách.

+ Bước 3. Chọn chữ số đứng thứ ba là một trong các chữ số 0,1,2,…,9 nên có 10cách.

+ Bước 4. Chọn chữ số đứng thứ tư là một trong các chữ số 0,1,2,…,9 nên có 10cách.

+ Bước 5. Chọn chữ số đứng cuối cùng là một chữ số chẵn 0,2,4,6,8 nên có 5 cách.

Theo quy tắc nhân, có 4×103×5=20000 số.

BÀI TẬP TRẮC NGHIỆM:

Câu 1: Số tam giác xác định bởi các đỉnh của một đa giác lồi có 13 đỉnh.

A.128    B.143    C.286    D.426

Lời giải:

Đáp án : C

Một tam giác được xác định nếu biết ba đỉnh của nó.

Do đó; số tam giác xác định bởi các đỉnh của đa giác lồi đã cho là: 

Câu 2: Một đa giác (H) có n cạnh. Biết rằng từ n đỉnh của đa giác ta lập được 816 tam giác. Tìm n?

A.18    B.17    C.16    D.14

Lời giải:

Đáp án : A

Do đa giác (H) có n cạnh nên đa giác này có n đỉnh .

Một tam giác được xác định nếu biết ba đỉnh của tam giác đó.

Do đó; từ n đỉnh của đa giác ta lập được số tam giác là: 

Theo giả thiết ta có: 

Câu 3: Cho một đa giác có 14 cạnh. Hỏi đa giác này có bao nhiêu đường chéo.

A.72    B.68    C.54    D.77

Lời giải:

Đáp án : D

Đa giác đã cho có 14 cạnh nên có 14 đỉnh.

Số đoạn thẳng được tạo ra từ 14 đỉnh này là: 

Mà đa giác này có 14 cạnh nên đa giác này có số đường chéo là:

91- 14= 77 đường chéo

Chú ý: Số cạnh+ số đường chéo =số đoạn thẳng nối 2 đỉnh bất kì.

Câu 4: Cho một đa giác có n đỉnh. Biết rằng đa giác này có 35 đường chéo. Tìm n?

A.7    B.8    C.10    D.12

Lời giải:

Đáp án : C

Do đa giác này có n đỉnh nên đa giác này có n cạnh.

Từ n đỉnh của đa giác ta có số đoạn thẳng có đầu mút; cuối mút là n đỉnh này là: 

⇒ Số đường chéo của đa giác là:

Theo giả thiết ta có: 

Vậy đa giác đã cho có 10 đỉnh

Câu 5: Số giao điểm tối đa của 18 đường thẳng phân biệt là:

A.306    B.324    C.153    D.174

Lời giải:

Đáp án :

Hai đường thẳng phân biệt có tối đa 1 giao điểm.

⇒ Số giao điểm tối đa của 18 đường thẳng là: 

Câu 6: Cho một đường tròn và 7 đường thẳng phân biệt. Hỏi có tối đa bao nhiêu giao điểm ?

A.28    B.14    C.21    D.35

Lời giải:

Đáp án : D

+ Ta tính số giao điểm tối đa của 7 đường thẳng với nhau:

Hai đường thẳng phân biệt có tối đa 1 giao điểm

⇒ số giao điểm tối đa của 7 đường thẳng là: 

+ Ta tính số giao điểm tối đa của 7 đường thẳng với đường tròn.

Một đường thẳng cắt đường tròn tối đa tại hai điểm

⇒ 7 đường thẳng cắt đường tròn tối đa: 2.7= 14 điểm

⇒ Số giao điểm tối đa của 5 đường thẳng và đường tròn là: 21+ 14= 35 điểm

Câu 7: Cho hai đường thẳng song song a và b. Trên đường thẳng a cho 8 điểm phân biệt, trên đường thẳng b cho 6 điểm phân biệt. Hỏi có bao nhiêu tam giác có các đỉnh là các điểm đã cho trên hai đường a và b.

A.364    B.231    C.288    D.210

Lời giải:

Đáp án : C

- Trường hợp 1. Tam giác có 2 đỉnh nằm trên a và 1 đỉnh thuộc b

   + Có 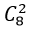 = 28 cách chọn 2 đỉnh thuộc đường thẳng a.

   + Có 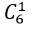 = 6 cách chọn 1 đỉnh thuộc b.

Theo quy tắc nhân có : 28. 6= 168 tam giác.

- Trường hợp 2. Tam giác có 1 đỉnh nằm trên a và 2 đỉnh thuộc b

   + Có 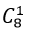 = 8 cách chọn 1 đỉnh thuộc đường thẳng a.

   + Có 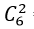 = 15 cách chọn 2 đỉnh thuộc b.

Theo quy tắc nhân có : 8. 15= 120 tam giác.

Kết hợp hai trường hợp ta có : 168 + 120= 288 tam giác.

Câu 8: Cho hai đường thẳng d₁ và d₂ song song với nhau. Trên d₁ có 9 điểm phân biệt, trên d₂ có n điểm phân biệt ( n>1). Biết có 540 tam giác có đỉnh là các điểm nói trên.Tìm n?

Lời giải:

Đáp án : C

- Trường hợp 1. Tam giác có 2 đỉnh nằm trên d₁ và 1 đỉnh thuộc d₂

   + Có 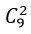 = 36 cách chọn 2 đỉnh thuộc đường thẳng d₁.

   + Có 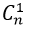 = n cách chọn 1 đỉnh thuộc d₂.

Theo quy tắc nhân có : 36.n tam giác.

- Trường hợp 2. Tam giác có 1 đỉnh nằm trên d₁ và 2 đỉnh thuộc d₂

   + Có 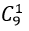 = 9 cách chọn1 đỉnh thuộc đường thẳng d₁.

   + Có 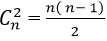 cách chọn 2 đỉnh thuộc d₂.

Theo quy tắc nhân có : 

Do đó ; số tam giác được tạo ra là : 

Theo đề bài ta có : 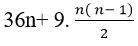= 540

Câu 9: Cho đa giác đều A₁A₂....A_2n nội tiếp trong đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm A₁ ;A₂ ;.... ; A_2n gấp 76/3 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm A₁ ;A₂ ;.... ; A_2n. Tìm n?

A.10    B.9    C.8    D.15

Lời giải:

Đáp án :

+ Số tam giác có đỉnh là 3 trong số 2n điểm đã cho là: 

+ Do đa giác đều A₁A₂....A_2n nội tiếp trong đường tròn tâm O nên các đoạn thẳng A₁A_n+1; A₂A_{n+ 2};...; A_nA_2n là n đường kính .

+ Số các hình chữ nhật có đỉnh là 4 trong 2n điểm A₁ ;A₂ ;.... ; A_2n là 

( Cứ hai đường kính cho ta một hình chữ nhật nên số các hình chữ nhật thỏa mãn chính bằng số cách chọn 2 đường kính trong n đường kính).

+ Theo đầu bài ta có phương trình :

Câu 10: Cho15 đường thẳng song song lần lượt cắt 12 đường thẳng song song khác. Hỏi có bao nhiêu hình bình hành được tạo thành từ các đường thẳng trên.

A.6290    B.6930    C.1440    D.5260

Lời giải:

Đáp án : B

Ta chia các đường thẳng đã cho thành 2 nhóm:

+ Nhóm 1: là 15 đường thẳng song song với nhau

+ Nhóm 2: là 10 đường thẳng song song với nhau

Tứ giác có các cạnh đối diện song song với nhau là hình bình hành.

+ Bước 1. Chọn 2 đường thẳng nhóm 1 có: 

+ Bước 2. Chọn 2 đường thẳng nhóm 2 có: 

Số hình bình hành được tạo ra là : 105. 66 = 6930 hình

Câu 11: Cho 5 đường tròn phân biệt và 4 đường thẳng phân biệt.Hỏi có tối đa bao nhiêu giao điểm giữa các đường tròn và đường thẳng?

A.66    B.34    C.60    D.Đáp án khác

Lời giải:

Đáp án : A

+ Bước 1. Ta tính số giao điểm tối đa của 5 đường tròn:

Hai đường tròn phân biệt có tối đa 2 điểm chung. Nên số giao điểm tối đa của 5 đường tròn là : 

+ Bước 2. Ta tính số giao điểm tối đa của 4 đường thẳng:

Hai đường thẳng phân biệt có tối đa 1 điểm chung nên số giao điểm tối đa của 4 đường thẳng này là : 

+ Bước 3. Số giao điểm tối đa của các đường tròn với các đường thẳng :

Một đường thẳng cắt đưởng tròn tối đa tại hai điểm.

⇒ 4 đường thẳng cắt 1 đường tròn tối đa tại: 4.2= 8 điểm

⇒ 4 đường thẳng cắt 5 đường tròn tối đa tại: 8.5= 40 điểm

Do đó; số giao điểm tối đa giữa các đường thẳng và đường tròn là : 20 + 6 + 40= 66 điểm

Câu 12: Trong mặt phẳng tọa độ cho đa giác (H): A₁A₂...A₁₆. Hỏi từ các đỉnh của đa giác (H) ta lập được bao nhiêu tam giác có đúng 1 cạnh của (H)?

Lời giải:

Đáp án : B

Đa giác A₁A₂...A₁₆ là đa giác có 16 đỉnh và có 16 cạnh .

Giả sử tam giác A_iA_jA_k ( 1≤i,j,k≤16) có đúng 1 cạnh của ( H).

Giả sử A_iA_j là một cạnh của ( H). Khi đó số cách chọn cạnh này là: 16 ( vì đa giác (H) có 16 cạnh).

Số cách chọn đỉnh còn lại A_k là 12 cách ( đỉnh này khác A_i; A_j và khác hai đỉnh liền kề với A_i,A_j )

Theo quy tắc nhân; số tam giác thỏa mãn là 16.12 = 192 tam giác.

Câu 13: Trong mặt phẳng cho đa giác đều (H) có 15 cạnh. Có bao nhiêu tam giác có 3 đỉnh là các đỉnh của (H) nhưng không có cạnh nào là cạnh của (H) ?

A.2760    B.1720    C.1600    D.1620

Lời giải:

Đáp án : D

Do đa giác đã cho có 15 cạnh nên đa giác này có 15 đỉnh là A₁; A₂; ..; A₁₅.

+ Bước 1. Chọn đỉnh thứ nhất A_i: có 15 cách.

+ Bước 2. Chọn đỉnh thứ hai A_j: đỉnh thứ 2 khác đỉnh thứ nhất và khác với đỉnh liền kề với A_i ( chú ý tam giác cần lập không có cạnh nào của ( H)) nên có 12 cách chọn đỉnh A_j

+ Bước 3. Chọn đỉnh thứ ba A_k: khác đỉnh thứ nhất - thứ hai; khác 2 đỉnh liền kề A_i; khác 2 đỉnh liền kề A_j nên có 9 cách chọn A_k.

Theo quy tắc nhân có: 15.12.9= 1620 tam giác thỏa mãn.

Xem thêm các dạng bài tập hay, có đáp án:

250 Bài tập về Hoán vị - Chỉnh hợp - Tổ hợp (có đáp án năm 2024)

100 Bài tập về Hoán vị – chỉnh hợp – tổ hợp (có đáp án năm 2024)

30 Bài tập về biến dị tổ hợp (2024) có đáp án chi tiết nhất

30 bài tập về Lý thuyết Số nguyên tố. Hợp số. Bảng số nguyên tố hay, chi tiết

50 Bài tập về Hoán vị - Chỉnh hợp - Tổ hợp (có đáp án năm 2024)