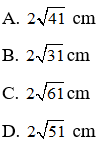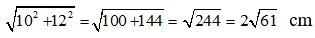Công thức tính diện tích hình chữ nhật (2024) chi tiết nhất

Công thức tính diện tích hình chữ nhật

1. Phương pháp giải

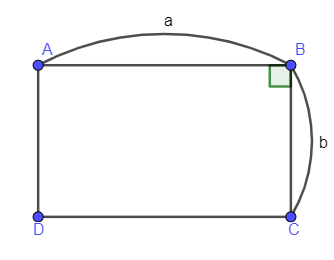
Diện tích hình chữ nhật bằng tích hai kích thước của nó (tích của chiều dài và chiều rộng).

 S = a.b (đơn vị diện tích)

Với a là chiều dài, b là chiều rộng hình chữ nhật.

Hình chữ nhật ABCD có AB = a; BC = b

$S_{ABCD}=AB.BC=a.b$ (đơn vị diện tích)

2. Ví dụ minh họa

Ví dụ 1: Tính diện tích hình chữ nhật có chiều dài là 5cm, chiều rộng là 3cm.

Lời giải:

Diện tích hình chữ nhật là:

$S=5.3=15c{m}^2$

Vậy diện tích hình chữ nhật cần tính là 15cm².

Ví dụ 2: Một thửa đất hình chữ nhật có chu vi và 200m, chiều dài gấp ba lần chiều rộng. Tính diện tích thửa đất đó.

Lời giải:

Gọi chiều rộng của thửa đất hình chữ nhật là x (m) (x > 0).

Vì chiều dài gấp ba lần chiều rộng nên chiều dài thửa đất là 3x (m).

Chu vi thửa đất hình chữ nhật là: (x + 3x).2 (m)

Mà chu vi thửa đất là 200m nên ta có:

(x + 3x).2 = 200

$$\begin{gathered} \iff 4x.2=200 \\ \iff 8x=200 \\ \iff x=200:8 \\ \iff x=25m \end{gathered}$$

Vì chiều dài bằng ba lần chiều rộng nên chiều dài thửa đất là: 3.25 = 75m

Diện tích thửa đất cần tính là:

S = 75.25 = 1875 (m²)

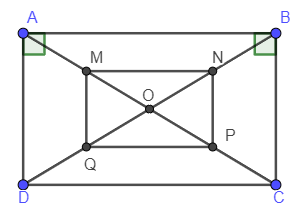
Ví dụ 3: Cho hình chữ nhật ABCD có AD = 7cm, BD = 25cm và O là giao điểm của hai đường chéo. Gọi M, N, P, Q theo thứ tự là trung điểm của OA, OB, OC, OD. Tính diện tích MNPQ.

Lời giải:

Vì ABCD là hình chữ nhật nên $\widehat{DAB}={90}^{\circ }$

Tam giác ABD vuông tại A ta có:

$A{D}^2+A{B}^2=B{D}^2$ (định lý Py – ta – go)

$$\begin{gathered} \iff 7^2+A{B}^2={25}^2 \\ \iff 49+A{B}^2=625 \\ \Rightarrow A{B}^2=625-49 \\ \Rightarrow AB=24cm \end{gathered}$$

Ta có: M là trung điểm của OA; N là trung điểm của OB nên MN là đường trung bình của tam giác OAB

$\Rightarrow MN//AB;MN=\frac{1}{2}AB$(Tính chất)  (1)

Lại có: P là trung điểm của OC; Q là trung điểm của OD nên PQ là đường trung bình của tam giác OCD

$\Rightarrow PQ//CD;PQ=\frac{1}{2}CD$  (Tính chất)  (2)

Lại có ABCD là hình chữ nhật nên AB // CD; AB = CD (Tính chất)  (3)

Từ (1); (2); (3) $\Rightarrow MN//PQ;MN=PQ$

Xét tứ giác MNPQ có:

MN // PQ

MN = PQ

Do đó tứ giác MNPQ là hình bình hành (dấu hiệu nhận biết).

Lại có M là trung điểm của OA; Q là trung điểm OD nên MQ là đường trung bình của tam giác OAD

 $\Rightarrow MQ//AD;MQ=\frac{1}{2}AD$(Tính chất)

Mà $AB\perp AD$

Do đó $MQ\perp AB$. Mặt khác $AB//MN$(chứng minh trên) nên $MN\perp MQ$ (quan hệ từ vuông góc đến song song).

$\Rightarrow \widehat{QMN}={90}^{\circ }$

Xét hình bình hành MNPQ có:

$\widehat{QMN}={90}^{\circ }$

Nên hình bình hành MNPQ là hình chữ nhật (dấu hiệu nhận biết).

Ta có: $MQ=\frac{1}{2}AD=\frac{1}{2}.7=\frac{7}{2}cm$

Diện tích hình chữ nhật MNPQ là:

$S=MQ.MN=\frac{7}{2}.12=42c{m}^2$.

3. Bài tập vận dụng

Bài 1: Diện tích hình chữ nhật thay đổi như thế nào nếu chiều rộng tăng 4 lần, chiều dài giảm 2 lần ?

   A. Diện tích không đổi.

   B. Diện tích giảm 2 lần.

   C. Diện tích tăng 2 lần.

   D. Cả đáp án A, B, C đều sai.

Lời giải:

Công thức diện tích hình chữ nhật là S_hcn = a.b

Trong đó : a là chiều dài, b là chiều rộng

Theo giả thiết: S_{ban đầu} = a.b

Khi đó ta có: S_sau = 4b.1/2a = 2a.b = 2S_{ban đầu}

Do đó, diện tích sau tăng lên 2 lần.

Chọn đáp án C.

Bài 2: Cho hình chữ nhật có chiều dài là 4 cm, chiều rộng là 1,5 cm. Diện tích của hình chữ nhật đó là ?

   A. 5( cm )   B. 6( cm² )

   C. 6( cm )   D. 5( cm² )

Lời giải:

Công thức diện tích hình chữ nhật là S_hcn = a.b

Trong đó : a là chiều dài, b là chiều rộng

Khi đó ta có: S_hcn = 4. 1,5 = 6( cm² ).

Chọn đáp án B.

Bài 3: Cho hình vuông có độ dài cạnh hình vuông là 4 cm. Diện tích của hình vuông đó là?

   A. 8( cm ).   B. 16( cm )

   C. 8( cm² )   D. 16( cm² )

Lời giải:

Diện tích hình vuông bằng bình phương cạnh của nó: S = a².

Khi đó ta có S_hv = 4.4 = 16 ( cm² ).

Chọn đáp án D.

Bài 4: Cho tam giác vuông, có độ dài hai cạnh góc vuông lần lượt là 6cm, 4cm. Diện tích của tam giác vuông đó là ?

   A. 24( cm² )   B. 14( cm² )

   C. 12( cm² )   D. 10( cm² )

Lời giải:

Diện tích tam giác vuông bằng nửa tích hai cạnh: S = 1/2a.b.

Khi đó ta có S = 1/2. 6. 4 = 12( cm² ).

Chọn đáp án C.

Bài 5: Cho hình vuông có đường chéo là 6( dm ) thì diện tích là ?

   A. 12( cm² )   B. 18( cm² )

   C. 20( cm² )   D. 24( cm² )

Lời giải:

Diện tích hình vuông bằng bình phương cạnh của nó: S = a².

Ngoài công thức này, diện tích hình vuông còn một công thức mở rông là:

Diện tích hình vuông bằng nửa tích của hai đường chéo

Khi đó ta có : S = 1/2. 6. 6 = 18( cm² ).

Chọn đáp án B.

Bài 6: Cho một tam giác vuông có độ dài hai cạnh góc vuông là 8cm và 9cm. Một hình vuông khác có diện tích bằng diện tích tam giác. Tính độ dài cạnh hình vuông.

   A. 6cm     B. 7cm

   C. 4cm     D. 8cm

Lời giải:

Diện tích tam giác vuông là: S = (1/2).8.9 = 36cm²

Gọi độ dài cạnh hình vuông là a (cm).

Diện tích hình vuông là: S = a² (cm²)

Vì diện tích hình vuông bằng diện tích tam giác nên: a² = 36 nên a = 6cm

Chọn đáp án A

Bài 7: Một hình chữ nhật có chiều rộng là 10cm và diện tích là 120cm². Tính đường chéo của hình chữ nhật?

Lời giải:

Diện tích hình chữ nhật là: S = a.b trong đó a và b lần lượt là chiều dài và chiều rộng của hình chữ nhật

Suy ra: 120 = a.10 nên a = 12

Đường chéo của hình chữ nhật là:

Chọn đáp án C

Xem thêm các dạng bài tập khác:

60 Bài tập về diện tích hình chữ nhật, diện tích hình vuông (có đáp án năm 2023)

50 Bài tập về Hình bình hành. Diện tích hình bình hành (có đáp án năm 2024)

60 Bài tập về Hình thoi. Diện tích hình thoi (có đáp án năm 2024)

50 Bài tập Hình thang. Diện tích hình thang (có đáp án năm 2024)

50 Bài tập Diện tích hình tròn (có đáp án năm 2024)