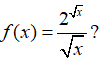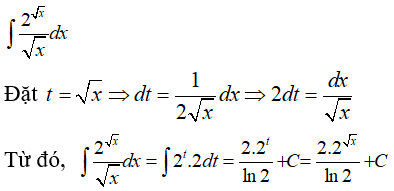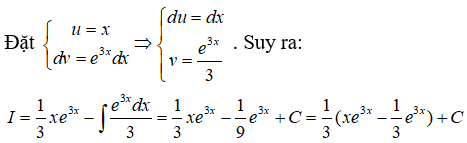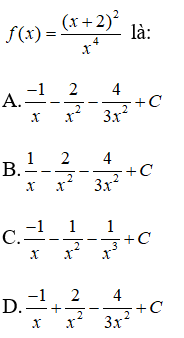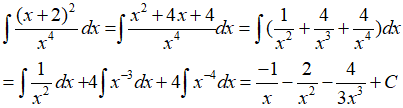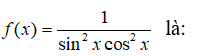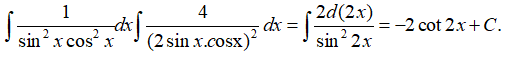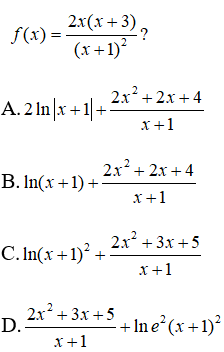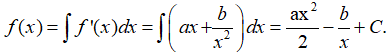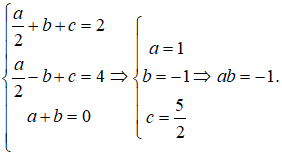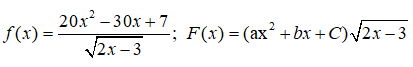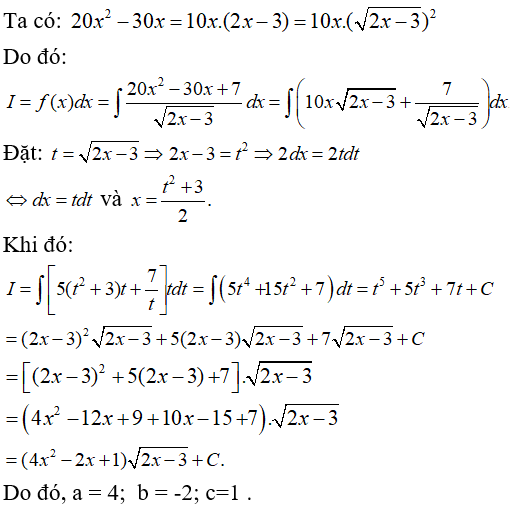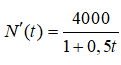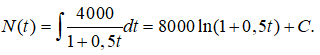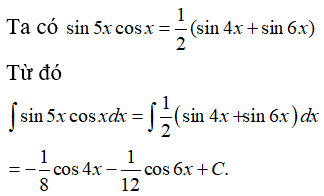Công thức nguyên hàm
I. Công thức
Bảng công thức nguyên hàm cơ bản

Bảng công thức nguyên hàm nâng cao:

Bảng công thức nguyên hàm mở rộng:

Bảng công thức nguyên hàm lượng giác:
II. Ví dụ minh hoạ
Ví dụ 1.1: Tìm nguyên hàm của các hàm số sau:
Lời giải:
| A. m = 3 | B. m = 0 | C. m = 1 | D. m = 2 |
Lời giải:
Chọn đáp án C.
III. Bài tập vận dụng
Bài 1: Hàm số nào sau đây không phải là một nguyên hàm của:
Lời giải:
Bài 2: Tìm I = ∫x.e3xdx
Lời giải:
Bài 3: Họ nguyên hàm của hàm số
Lời giải:
Bài 4: Họ nguyên hàm của hàm số
Lời giải:
Bài 5: Hàm số nào dưới đây không là nguyên hàm của
Lời giải:
Bài 6: Họ nguyên hàm của hàm số f(x) = (2 tanx + cotx)2 là:
Lời giải:
∫(2tanx + cotx)2dx = ∫(4tan2x + 2tanx.cotx + cot2x)dx
= ∫ [4(tan2x + 1) + (cot2x + 1) - 1]dx
= 4tanx = cotx - x + C
Bài 7: Biết rằng: f'(x) = ax + , f(-1) = 2, f(1) = 4, f'(1) = 0. Giá trị biểu thức ab bằng?
Lời giải:
Ta có:
Từ điều kiện đã cho ta có phương trình sau:
Bài 8: Cho các hàm số:
với x > . Để F(x) là một nguyên hàm của f(x) thì giá trị của a,b,c lần lượt là:
Lời giải:
Ta có:
Bài 9: Một đám vi khuẩn tại ngày thứ t có số lượng là N(t). Biết rằng
và lúc đầu đám vi khuẩn có 250000 con. Sau 10 ngày số lượng vi khuẩn xấp xỉ bằng:
Lời giải:
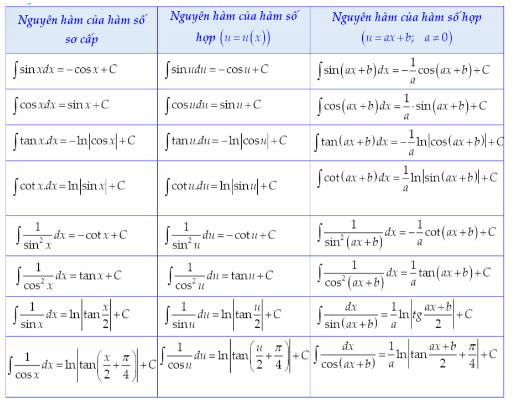
Số lượng vi khuẩn tại ngày thứ t bằng
Với t = 0 ta có: N(0) = 250000,
Vậy N(t) = 8000.ln(1 + 0,5t) + 250000
khi đó N(10) ≈ 264334.
Bài 10: Tìm I = ∫sin5xcosxdx .
Lời giải:
Xem thêm các dạng bài tập hay, có đáp án:
30 Bài tập về Cách tìm nguyên hàm của hàm số mũ, hàm số logarit (2024) cực hay, có đáp án
40 Bài tập Tìm nguyên hàm của hàm đa thức, hàm phân thức (2024) có đáp án