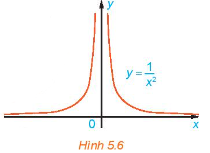
Xét hàm số f( x ) = 1/x^2 có đồ thị như Hình 5.6. Cho xn = 1/n, chứng tỏ rằng f(xn) ⟶ +∞.
Xét hàm số \(f\left( x \right) = \frac{1}{{{x^2}}}\) có đồ thị như Hình 5.6.
Cho \({x_n} = \frac{1}{n}\), chứng tỏ rằng f(xn) ⟶ +∞.
Lời giải:
Ta có: \({x_n} = \frac{1}{n}\), do đó \(f\left( {{x_n}} \right) = \frac{1}{{x_n^2}} = \frac{1}{{{{\left( {\frac{1}{n}} \right)}^2}}} = {n^2}\).
Vì n ⟶ +∞ nên \({x_n} = \frac{1}{n} \to 0\) và f(xn) ⟶ +∞.