Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện

Vận dụng trang 37 Toán 10 Tập 1: Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay người đó ở độ cao bao nhiêu mét?

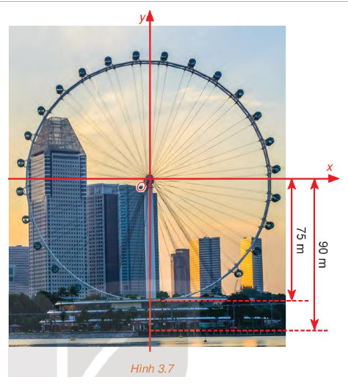
Trả lời

Giả sử chiếc đu quay quay theo chiều kim đồng hồ.

Gọi M là vị trí thấp nhất của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A, A’, B, H (như hình vẽ).

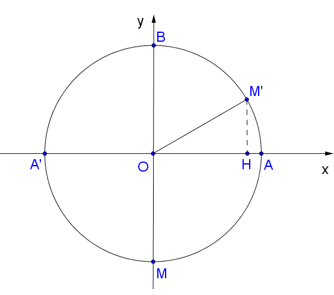
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng $\frac{2}{3}$ chu vi đường tròn.

Sau 15 phút, cabin di chuyển từ điểm M đến điểm B, đi được $\frac{1}{2}$ chu vi đường tròn.

Trong 5 phút tiếp theo, cabin đi chuyển từ điểm B đến điểm M’ tương ứng $\frac{1}{6}$ chu vi đường tròn hay $\frac{1}{3}$ cung tròn $\stackrel{⏜}{A\text{'}A}$.

Do đó: $\widehat{BOM\text{'}}=\frac{1}{3}.{180}^o={60}^o$

$\Rightarrow \widehat{AOM\text{'}}={90}^o-{60}^o={30}^o$

Ta có $M\text{'}H=\sin {30}^o.OM\text{'}=\frac{1}{2}.75=37,5$ (m).

Do đó, độ cao của người đó là:

37,5 + 90 = 127,5 (m).

Vậy sau 20 phút quay người đó ở độ cao 127,5 m.

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 4: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Bài 6: Hệ thức lượng trong tam giác

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu