Câu hỏi:
19/01/2024 54Trong sơ đồ, chùm sáng S hướng vào gương màu xanh, phản xạ vào gương màu đỏ và sau đó phản xạ vào gương màu xanh như hình vẽ. Biết OP = 2 m, m.
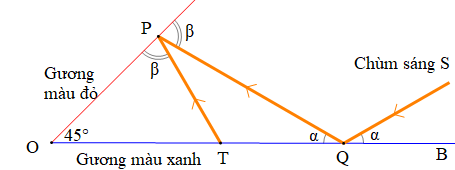
Khi đó đoạn PT bằng:
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
Áp dụng định lí côsin trong tam giác OPQ ta có:
PQ2 = OP2 + OQ2 – 2.OP.OQ.cos
Þ PQ2 = 8
Áp dụng hệ quả định lí côsin trong tam giác OPQ ta có:
Þ α = 30°
Xét tam giác POQ có: β = 45° + α (tính chất góc ngoài của tam giác)
Þ β = 45° + 30° = 75°
Xét tam giác OTP ta có: (định lí tổng ba góc trong tam giác)
Hay
Áp dụng định lí sin cho tam giác OTP ta có:
Vậy
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
Áp dụng định lí côsin trong tam giác OPQ ta có:
PQ2 = OP2 + OQ2 – 2.OP.OQ.cos
Þ PQ2 = 8
Áp dụng hệ quả định lí côsin trong tam giác OPQ ta có:
Þ α = 30°
Xét tam giác POQ có: β = 45° + α (tính chất góc ngoài của tam giác)
Þ β = 45° + 30° = 75°
Xét tam giác OTP ta có: (định lí tổng ba góc trong tam giác)
Hay
Áp dụng định lí sin cho tam giác OTP ta có:
Vậy
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).
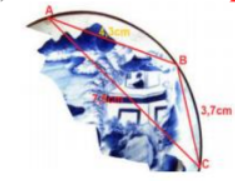
Bán kính của chiếc đĩa này bằng (kết quả làm tròn đến chữ số thập phân thứ hai):
Câu 2:
Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù.
Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù.
Câu 3:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
Câu 4:
Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
Câu 5:
Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
Câu 8:
Một tam giác có ba cạnh là 52, 56, 60. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác. Khi đó R. r bằng:
Một tam giác có ba cạnh là 52, 56, 60. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác. Khi đó R. r bằng:
Câu 9:
Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai?
Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai?
Câu 10:
Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Diện tích tam giác GEC là:
Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Diện tích tam giác GEC là:
Câu 11:
Tam giác ABC có góc B tù, AB = 3, AC = 4 và có diện tích bằng . Số đo góc A là:
Tam giác ABC có góc B tù, AB = 3, AC = 4 và có diện tích bằng . Số đo góc A là:
Câu 12:
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số là:
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số là:
Câu 14:
Cho tam giác ABC có BC = a, CA = b, AB = c. Mệnh đề nào sau đây là đúng?
Câu 15:
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.
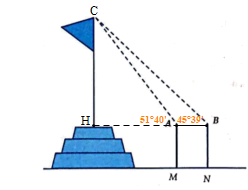
Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là:


