Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M0(x0; y0) và có vectơ pháp tuyến n = (a;b). Xét điểm M(x; y) nằm trên ∆ (Hình 28)

Hoạt động 4 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và có vectơ pháp tuyến $\overrightarrow{n}=\left(a;b\right)$. Xét điểm M(x; y) nằm trên ∆ (Hình 28)

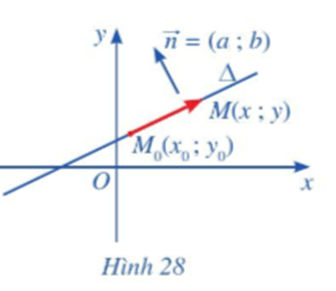
a) Nhận xét về phương của hai vectơ $\overrightarrow{n}$ và $\overrightarrow{M_{0}M}$.

b) Tìm mối liên hệ giữa tọa độ của điểm M với tọa độ của điểm M₀ và tọa độ của vectơ pháp tuyến $\overrightarrow{n}$.

Trả lời

a) Vectơ $\overrightarrow{n}$ là vectơ pháp tuyến của đường thẳng ∆ nên giá của vectơ $\overrightarrow{n}$ vuông góc với đường thẳng ∆.

Đường thẳng ∆ đi qua điểm M₀ và M, nên đường thẳng ∆ chính là đường thẳng MM₀. Khi đó vectơ $\overrightarrow{M_{0}M}$ có giá chính là đường thẳng ∆.

Do đó giá của vectơ $\overrightarrow{n}$ và giá của vectơ $\overrightarrow{M_{0}M}$ vuông góc với nhau.

Vậy hai vectơ hai vectơ $\overrightarrow{n}$ và $\overrightarrow{M_{0}M}$ không cùng phương.

b) Ta có: $\overrightarrow{M_{0}M}=\left(x-x_0;y-y_0\right),\overrightarrow{n}=\left(a;b\right)$.

Xét điểm M(x; y) thuộc ∆. Vì $\overrightarrow{M_{0}M}\perp \overrightarrow{n}$ nên

$\overrightarrow{M_{0}M}.\overrightarrow{n}=0\iff$a(x – x₀) + b(y – y₀) = 0 ⇔ ax + by – ax₀ – by₀ = 0.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 1: Tọa độ của vectơ

Bài 2: Biểu thức tọa độ của các phép toán vectơ

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic