Câu hỏi:
29/12/2023 85Trong mặt phẳng tọa độ Oxy, cho ba điểm A(0; – 1), B(1; 4), C(– 6; 5) không thẳng hàng. Tọa độ điểm D thỏa mãn ACBD là hình thang có AC // BD và AC = 2BD là:
A. D(7; –1);
B. D(4; 1);
C. D(–2; 7);
D. D(– 4; –1).
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
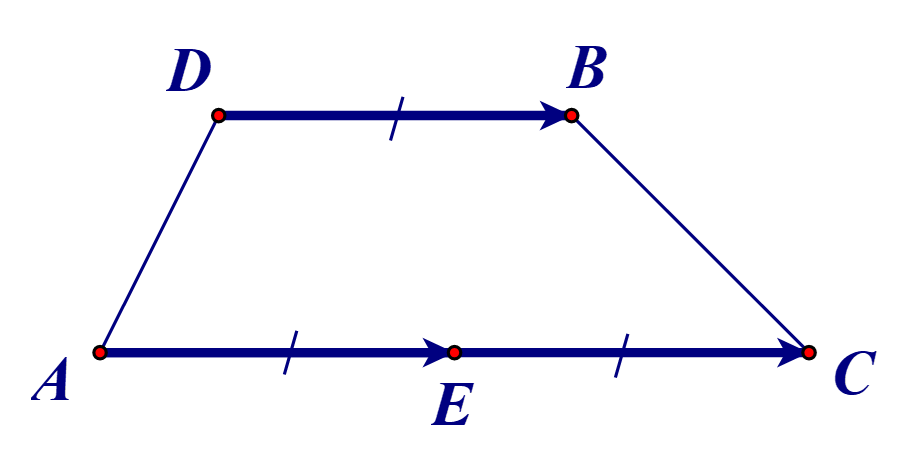
Gọi E(a; b) là trung điểm của AC.
Suy ra \(\overrightarrow {AE} = \overrightarrow {EC} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} - {x_A} = {x_C} - {x_E}\\{y_E} - {y_A} = {y_C} - {y_E}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} - 0 = - 6 - {x_E}\\{y_E} - \left( { - 1} \right) = 5 - {y_E}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2{x_E} = - 6\\2{y_E} = 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} = - 3\\{y_E} = 2\end{array} \right.\)
Suy ra E(–3; 2).
Gọi D(xD; yD).
Ta có AE = \(\frac{1}{2}AC\) = DB.
Ta có AE // DB (giả thiết) và AE = DB (chứng minh trên).
Suy ra \(\overrightarrow {DB} = \overrightarrow {AE} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_B} - {x_D} = {x_E} - {x_A}\\{y_B} - {y_D} = {y_E} - {y_A}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}1 - {x_D} = - 3 - 0\\4 - {y_D} = 2 - \left( { - 1} \right)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 4\\{y_D} = 1\end{array} \right.\)
Suy ra D(4; 1).
Vậy ta chọn phương án B.
Hướng dẫn giải
Đáp án đúng là: B
Gọi E(a; b) là trung điểm của AC.
Suy ra \(\overrightarrow {AE} = \overrightarrow {EC} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} - {x_A} = {x_C} - {x_E}\\{y_E} - {y_A} = {y_C} - {y_E}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} - 0 = - 6 - {x_E}\\{y_E} - \left( { - 1} \right) = 5 - {y_E}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2{x_E} = - 6\\2{y_E} = 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} = - 3\\{y_E} = 2\end{array} \right.\)
Suy ra E(–3; 2).
Gọi D(xD; yD).
Ta có AE = \(\frac{1}{2}AC\) = DB.
Ta có AE // DB (giả thiết) và AE = DB (chứng minh trên).
Suy ra \(\overrightarrow {DB} = \overrightarrow {AE} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_B} - {x_D} = {x_E} - {x_A}\\{y_B} - {y_D} = {y_E} - {y_A}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}1 - {x_D} = - 3 - 0\\4 - {y_D} = 2 - \left( { - 1} \right)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 4\\{y_D} = 1\end{array} \right.\)
Suy ra D(4; 1).
Vậy ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trên mặt phẳng tọa độ Oxy, cho hai điểm A(1; –1), B(2; 4). Để tứ giác OBMA là hình bình hành thì tọa độ M là:
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có D(3; 4), E(6; 1), F(7; 3) lần lượt là trung điểm của các cạnh AB, BC, CA. Tổng tung độ ba đỉnh của tam giác ABC là:
Câu 3:
Cho \(\vec u = \left( {{m^2} + 3;2m} \right)\), \(\vec v = \left( {5m - 3;{m^2}} \right)\). Nếu \(\vec u = \vec v\) thì m thuộc tập hợp:
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(4; – 1), B (7; 8). Tọa độ của điểm C là điểm đối xứng của A qua B là:
