Trong mặt phẳng (P) cho tam giác ABC có AB = 1, AC = 2, . Điểm S thay đổi thuộc đường thẳng đi qua A và vuông góc với (P), (S khác A). Gọi B1, C1 lần lượt là hình chiếu vuông góc của A trên S

42 15/06/2024

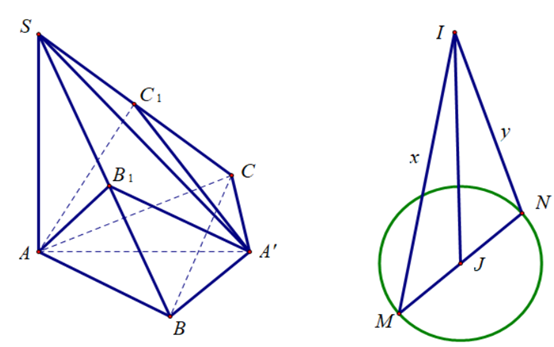
Trong mặt phẳng (P) cho tam giác ABC có AB = 1, AC = 2, $\hat{B A C} = 60^{\circ}$ . Điểm S thay đổi thuộc đường thẳng đi qua A và vuông góc với (P), (S khác A). Gọi B₁, C₁ lần lượt là hình chiếu vuông góc của A trên SB, SC. Đường kính MN thay đổi của mặt cầu (T) ngoại tiếp khối đa diện ABCB₁C₁ và I là điểm cách tâm mặt cầu (T) một khoảng bằng ba lần bán kính. Tính giá trị nhỏ nhất của IM + IN.

A. $6 \sqrt{3}$

B. $\sqrt{20}$

C. 6

D. $2 \sqrt{10}$

Trả lời

Chọn C

Trong mặt phẳng (P) cho tam giác ABC có AB = 1, AC = 2, . Điểm S thay đổi thuộc đường thẳng đi qua A và vuông góc với (P), (S khác A). Gọi B1, C1 lần lượt là hình chiếu vuông góc của A trên SB, SC. (ảnh 1)

Ta có $B C^{2} = A B^{2} + A C^{2} - 2 A B . A C . \cos A = 3 \Rightarrow B C = \sqrt{3}$ .

Bán kính đường tròn ngoại tiếp tam giác ABC: $R = \frac{B C}{2 \sin A} = 1$ .

Gọi J là tâm đường tròn ngoại tiếp tam giác ABC, A' là điểm đối xứng của A qua J.

Ta dễ dàng chứng minh được: $A C ⊥ A^{'} C, A B ⊥ A^{'} B, A B_{1} ⊥ A^{'} B_{1}, A C_{1} ⊥ A^{'} C_{1} \Rightarrow A, B, C, A_{1}, B_{1}$ đều thuộc mặt cầu tâm J, đường kính $A A^{'} = 2 R = 2 = M N$ .

Đặt $I M = x, I N = y; x, y \in [2; 4]$ .

+ Nếu I, J, M, N thẳng hàng thì $[\begin{array}{l} x = 2, y = 4 \\ x = 4, y = 2 \end{array} \Rightarrow x^{2} + y^{2} = 20$ .

+ Nếu I, J, M, N không thẳng hàng thì

$I J^{2} = \frac{x^{2} + y^{2}}{2} - \frac{M N^{2}}{4} \Leftrightarrow x^{2} + y^{2} = 2 (I J^{2} + \frac{M N^{2}}{4}) = 2 (9 + 1) = 20$ .

Vậy, ta luôn có: $x^{2} + y^{2} = 20$ .

Do $x, y \in [2; 4] \Rightarrow (x - 2) (y - 2) \geq 0 \Leftrightarrow x y \geq 2 (x + y) - 4$ .

$x^{2} + y^{2} = 20 \Leftrightarrow {(x + y)}^{2} - 20 = 2 x y \geq 4 (x + y) - 8 \Rightarrow {(x + y)}^{2} - 4 (x + y) - 12 \geq 0 \Leftrightarrow x + y \geq 6$ .

Vậy $\min (x + y) = 6 \Leftrightarrow [\begin{array}{l} x = 2 \Rightarrow y = 4 \\ y = 2 \Rightarrow x = 4 \end{array}$ .

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

Câu hỏi cùng chủ đề

Trong hệ trục tọa độ Oxyz cho 3 điểm A(5;-2;0), B(4;5;-2) và C(0;3;2). Điểm M di chuyển trên trục Ox. Đặt

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

60 4 tháng trước

Cho x và y là các số thực. Giá trị nhỏ nhất của biểu thức P = (y - 10^x) ^2022 + (e^y - xln10)^ 2022

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

35 4 tháng trước

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;100] để bất phương trình 4^ 2x - m - 4. 2^3x - 2m + 4. 2^x -m < 1 , nghiệm đúng với ?

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

55 4 tháng trước

Có bao nhiêu giá trị nguyên của tham số m thuộc -25; 0 sao cho hàm số y = x^4 - 5 e^x - mx^2 - m^2 - m x + 2 luôn đồng biến trên khoảng

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

44 4 tháng trước

Cho hàm số y = f(x) thỏa mãn f(0) = 0, f(x) + f'(x) = 1, với x thuộc R . Giá trị của f(ln2) bằng

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

36 4 tháng trước

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi góc anpha là mặt phẳng đi qua CD’ và tạo với mặt phẳng (A'B'C'D') một góc

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

35 4 tháng trước

Cho hai khối cầu có tổng diện tích bằng 80 pi tiếp xúc ngoài nhau và cùng tiếp xúc với mặt phẳng (P) lần lượt tại hai điểm A, B. Tính tổng thể tích của hai khối cầu đó biết AB = 4 căn bậc hai

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

35 4 tháng trước

Cho hàm số bậc ba y = f(x). Hàm số g(x) = f(x + 2) có bảng biến thiên như bên dưới. Tổng tất cả các giá trị nguyên của tham số m để tập nghiệm của phương trình

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

49 4 tháng trước

Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật với AB = 2a, BC = a. Biết góc A'AB = 90 độ và AA' = a căn bậc hai 5, CA' = 2a căn bậc hai 2. Thể tích khối hộp ABCD.A'B'C'D' bằng

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

42 4 tháng trước

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới. Số nghiệm thực phân biệt của phương trình f[f(x) + 1] + 2 = 0 là

(2023) Đề thi thử Toán THPT Liên Trường Nghê An có đáp án

59 4 tháng trước

Xem tất cả

Trong mặt phẳng (P) cho tam giác ABC có AB = 1, AC = 2, . Điểm S thay đổi thuộc đường thẳng đi qua A và vuông góc với (P), (S khác A). Gọi B1, C1 lần lượt là hình chiếu vuông góc của A trên S

Trả lời

Câu hỏi cùng chủ đề

Trong hệ trục tọa độ Oxyz cho 3 điểm A(5;-2;0), B(4;5;-2) và C(0;3;2). Điểm M di chuyển trên trục Ox. Đặt

Cho x và y là các số thực. Giá trị nhỏ nhất của biểu thức P = (y - 10^x) ^2022 + (e^y - xln10)^ 2022

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;100] để bất phương trình 4^ 2x - m - 4. 2^3x - 2m + 4. 2^x -m < 1 , nghiệm đúng với ?

Có bao nhiêu giá trị nguyên của tham số m thuộc -25; 0 sao cho hàm số y = x^4 - 5 e^x - mx^2 - m^2 - m x + 2 luôn đồng biến trên khoảng

Cho hàm số y = f(x) thỏa mãn f(0) = 0, f(x) + f'(x) = 1, với x thuộc R . Giá trị của f(ln2) bằng

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi góc anpha là mặt phẳng đi qua CD’ và tạo với mặt phẳng (A'B'C'D') một góc

Cho hai khối cầu có tổng diện tích bằng 80 pi tiếp xúc ngoài nhau và cùng tiếp xúc với mặt phẳng (P) lần lượt tại hai điểm A, B. Tính tổng thể tích của hai khối cầu đó biết AB = 4 căn bậc hai

Cho hàm số bậc ba y = f(x). Hàm số g(x) = f(x + 2) có bảng biến thiên như bên dưới. Tổng tất cả các giá trị nguyên của tham số m để tập nghiệm của phương trình

Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật với AB = 2a, BC = a. Biết góc A'AB = 90 độ và AA' = a căn bậc hai 5, CA' = 2a căn bậc hai 2. Thể tích khối hộp ABCD.A'B'C'D' bằng

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới. Số nghiệm thực phân biệt của phương trình f[f(x) + 1] + 2 = 0 là

Danh mục