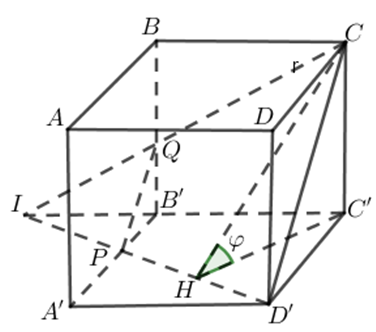
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi góc anpha là mặt phẳng đi qua CD’ và tạo với mặt phẳng (A'B'C'D') một góc
66
15/06/2024
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi là mặt phẳng đi qua CD’ và tạo với mặt phẳng (A'B'C'D') một góc với . Mặt phẳng chia khối lặp phương thành hai khối đa diện có thể tích là với . Tính V1.
A.
B.
C.
D.
Trả lời
Chọn D
Mặt phẳng là mặt phẳng đi qua CD’ và cắt C'B' tại I .
Kẻ .
Ta có vuông tại .
Ta có vuông tại .
Ta thấy với C'I = 2a thì nên Q là trung điểm BB'.
nên P là trung điểm A'B'.
Ta có:
Vì .
Vậy .