Trong mặt phẳng ( P ) cho hình bình hành ABCD. Gọi Ax, By, Cz, Dt lần lượt là các đường thẳng song song với nhau đi qua A, B, C, D và nằm về cùng một phía của mặt phẳng ( P ) đồng thời không
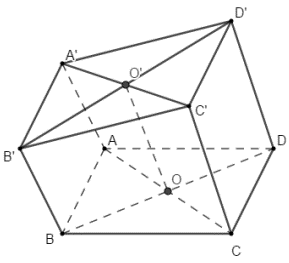
Trong mặt phẳng \(\left( P \right)\) cho hình bình hành ABCD. Gọi Ax, By, Cz, Dt lần lượt là các đường thẳng song song với nhau đi qua A, B, C, D và nằm về cùng một phía của mặt phẳng \(\left( P \right)\) đồng thời không nằm trong \(\left( P \right)\). Một mặt phẳng \(\left( \alpha \right)\) lần lượt cắt Ax, By, Cz, Dt tại \(A'\), \(B'\), \(C'\), \(D'\) biết \(BB' = 5,2\,cm\), \(CC' = 8,6\,cm\), \[DD' = 7,8\,cm\]. Tính \[AA'\].
A. 6cm.
B. 21,6cm
C. 11,2cm.
D. 4,4cm.