Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm O. Gọi M, N, E lần lượt là trung điểm của AB, BC, SO.

 a) Xác định thiết diện của hình chóp $S.ABCD$ cắt bởi mặt phẳng $\left( {MNE} \right)$.

 b) Mặt phẳng $\left( {MNE} \right)$ cắt SD tại K, tính tỉ số $\frac{{KS}}{{KD}}$.

Giải chi tiết:

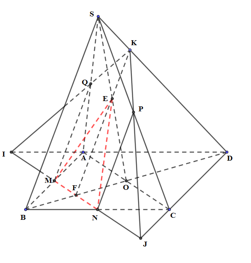
a) Trong (ABCD), gọi $I = MN \cap AD,$$J = MN \cap CD$, $F = MN \cap BD$

Trong (SBD), gọi $K = EF \cap SD$

Trong (SAD), gọi $Q = IK \cap SA$

Trong (SAD), gọi $P = JK \cap SC$

Khi đó, thiết diện của hình chóp $S.ABCD$ cắt bởi mặt phẳng $\left( {MNE} \right)$ là ngũ giác $MNPKQ$

b) MN là đường trung bình của $\Delta ABC \Rightarrow MN//AC$

$\Rightarrow MF{\rm{//}}AC \Rightarrow$ F là trung điểm của OB $\Rightarrow BF = \frac{1}{2}OB = \frac{1}{4}BD \Rightarrow BF = \frac{1}{3}FD$

Xét $\Delta SOB$ có: E, F lần lượt là trung điểm của SO, OB $\Rightarrow EF$ là đường trung bình của $\Delta SOB$

$\Rightarrow EF{\rm{//}}SB \Rightarrow FK{\rm{//}}SB \Rightarrow \frac{{KS}}{{KD}} = \frac{{BF}}{{DF}} = \frac{1}{3}$

Vậy, $\frac{{KS}}{{KD}} = \frac{1}{3}$