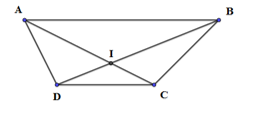
Cho hình thang ABCD có vecto DC = 1/2 vecto AB. Gọi I là giao điểm của hai đường chéo AC và BD. Phép vị tự nào dưới đây biến đường thẳng AB thành đường thẳng CD? A. V( I;k = - 1/2)
Cho hình thang ABCD có →DC=12→AB. Gọi I là giao điểm của hai đường chéo AC và BD. Phép vị tự nào dưới đây biến đường thẳng AB thành đường thẳng CD?
A. V(I;k=−12)
B. V(I;k=12)
C. V(I;k=−2)
D. V(I;k=13)