Đáp án đúng là: C

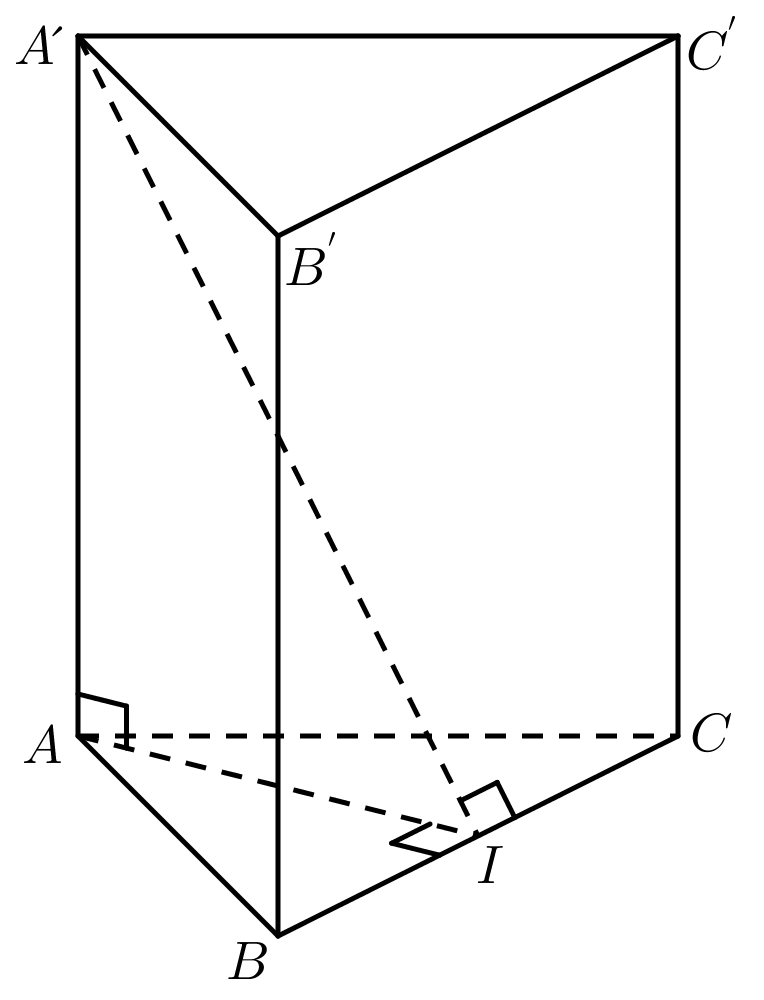
Gọi I là trung điểm của BC.

Do tam giác ABC đều nên $AI\perp BC\Rightarrow A^{\text{'}}I\perp BC\Rightarrow I$  là hình chiếu của A' trên BC. Vì $B,C\in Oz$  nên I là hình chiếu của A' trên $Oz\Rightarrow I\left(0;0;1\right)$ .

Ta có $\overrightarrow{A^{\text{'}}I}=\left(-\sqrt{3};1;0\right)\Rightarrow A^{\text{'}}I=2$ .

Trong tam giác vuông AA'I có: $AI=\sqrt{A^{\text{'}}{I}^2-A{A^{\text{'}}}^2}=\sqrt{4-1}=\sqrt{3}$ .

Vì tam giác ABC đều nên $BC=\frac{2}{\sqrt{3}}AI=\frac{2}{\sqrt{3}}.\sqrt{3}=2\Rightarrow CI=1$ .

Gọi $C\left(0;0;c\right)\in Oz$ .

Do $CI=1;I\left(0;0;1\right);C\ne O\Rightarrow C\left(0;0;2\right)\Rightarrow \overrightarrow{A^{\text{'}}C}\left(-\sqrt{3};1;1\right)$ .

Mà $\overrightarrow{u}=\left(a;b;2\right)$  là một vectơ chỉ phương của đường thẳng A'C nên $\overrightarrow{A^{\text{'}}C}$  và $\overrightarrow{u}$  cùng phương.

Suy ra $\frac{a}{-\sqrt{3}}=\frac{b}{1}=\frac{2}{1}\Rightarrow \left\{\begin{array}{l}a=-2\sqrt{3}\\ b=2\end{array}\right.\Rightarrow a^2+b^2={\left(-2\sqrt{3}\right)}^2+2^2=16$ .