Có tất cả bao nhiêu giá trị nguyên của tham số m nằm trong khoảng (-2023;2023) để hàm số y = 2023/(mlog3^2(x) - 4log3(x) + m + 3) xác định

A. 4040

B. 4044

C. 4039

D. 4046

Trả lời

Đáp án đúng là: C

Điều kiện: x > 0 .

Hàm số đã cho xác định trên $\left(0;+\infty \right)$  thì $m{\log }_3^{2}x-4{\log }_{3}x+m+3\ne \mathrm{0,}\forall x\in \left(0;+\infty \right)$ 

$\iff m\left({\log }_3^{2}x+1\right)\ne 4{\log }_{3}x-\mathrm{3,}\forall x\in \left(0;+\infty \right)$$\iff m\ne \frac{4{\log }_{3}x-3}{{\log }_3^{2}x+1},\forall x\in \left(0;+\infty \right)$

Để hàm số $y=\frac{2023}{m{\log }_3^{2}x-4{\log }_{3}x+m+3}$  xác định trên khoảng $\left(0;+\infty \right)$  thì phương trình $m=\frac{4{\log }_{3}x-3}{{\log }_3^{2}x+1}$  vô nghiệm trên khoảng $\left(0;+\infty \right)$ .

Xét hàm số $y=\frac{4t-3}{t^2+1}$  với $t={\log }_{3}x$

Khi đó $y^{\text{'}}=\frac{-4t^2+6t+4}{{\left(t^2+1\right)}^2}$ ; $y^{\text{'}}=0\Rightarrow -4t^2+6t+4=0\iff \left[\begin{array}{l}t=-\frac{1}{2}\\ t=2\end{array}\right.$ .

Ta có $\underset{t\to -\infty }{\lim }y=\underset{t\to -\infty }{\lim }y=0$ .

Bảng biến thiên

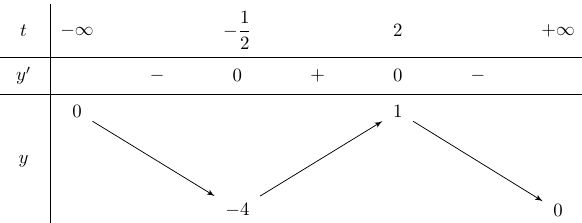
Dựa vào bảng biến thiên suy ra $m\in \left(-\infty ;-4\right)\cup \left(1;+\infty \right)$ .

Kết hợp điều kiện $m\in \left(-2023;2023\right)\Rightarrow m\in \left(-2023;-4\right)\cup \left(1;2023\right)$ .

Vì $m\in \mathbb{Z}$  suy ra có 4039 giá trị m  thỏa mãn.